Unit 4 2 Variable Quantitative Scatter Plots Standards

Unit 4 (2 -Variable Quantitative): Scatter Plots Standards: SDP 1. 0 and 1. 2 Objective: Determine the correlation of a scatter plot

Scatter Plot • A scatter plot is a graph of a collection of ordered pairs (x, y). • The graph looks like a bunch of dots, but some of the graphs are a general shape or move in a general direction.

Scatter Plots • Summarizes the relationship between two quantitative variables. • Horizontal axis represents one variable and vertical axis represents second variable. • Plot one point for each pair of measurements.
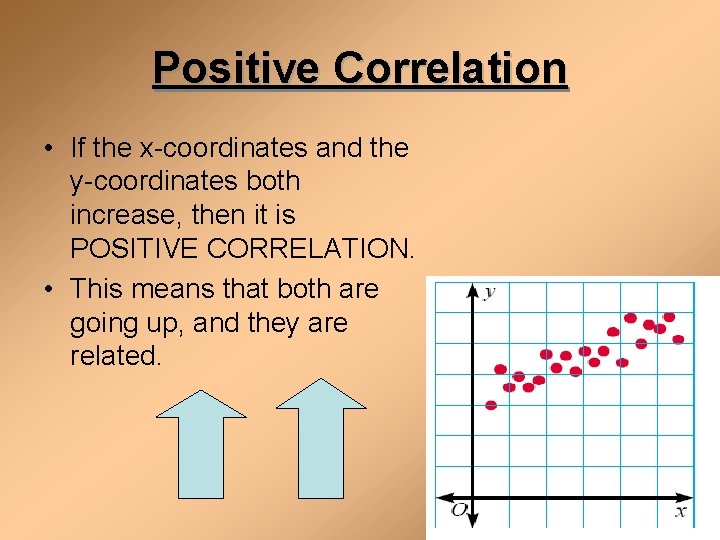
Positive Correlation • If the x-coordinates and the y-coordinates both increase, then it is POSITIVE CORRELATION. • This means that both are going up, and they are related.

Positive Correlation • If you look at the age of a child and the child’s height, you will find that as the child gets older, the child gets taller. Because both are going up, it is positive correlation. Age 1 Height 25 “ 2 3 31 34 4 36 5 40 6 41 7 47 8 55
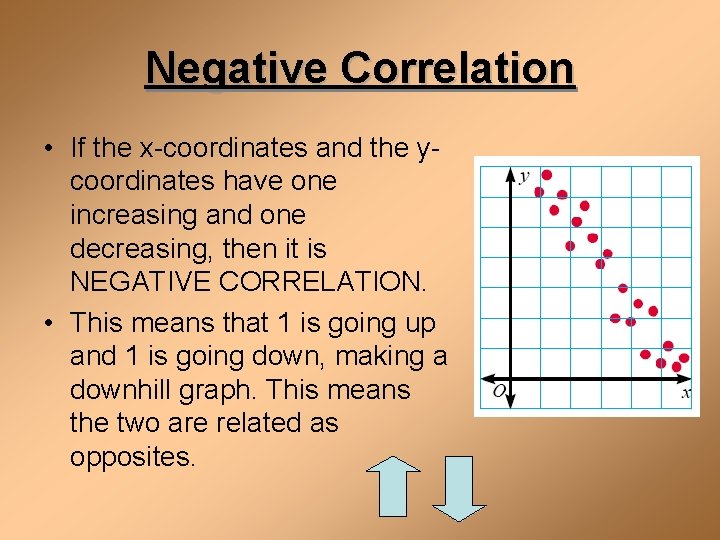
Negative Correlation • If the x-coordinates and the ycoordinates have one increasing and one decreasing, then it is NEGATIVE CORRELATION. • This means that 1 is going up and 1 is going down, making a downhill graph. This means the two are related as opposites.

Negative Correlation • If you look at the age of your family’s car and its value, you will find as the car gets older, the car is worth less. This is negative correlation. Age 1 of car 2 3 4 5 Value $30, 000 $27, 00 $23, 50 $18, 70 $15, 35 0 0

No Correlation • If there seems to be no pattern, and the points looked scattered, then it is no correlation. • This means the two are not related.

No Correlation • If you look at the size shoe a baseball player wears, and their batting average, you will find that the shoe size does not make the player better or worse, then are not related.

Correlation Coefficient A number, r, from -1 to 1 that measures how well a line fits a set of data points. -1 – strong negative correlation -0. 5 – weak negative corr. 0 – no correlation 0. 5 – weak positive corr. 1 – strong positive corr.
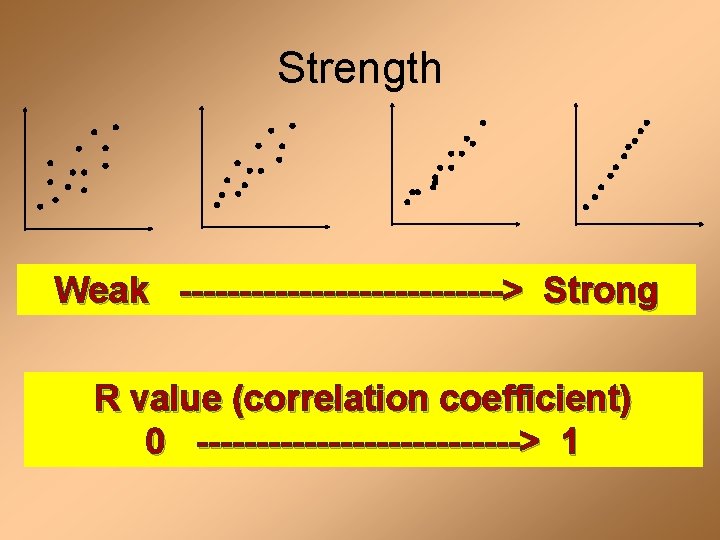
Strength Weak --------------> Strong R value (correlation coefficient) 0 --------------> 1

Put the correlation coefficients in order from weakest to strongest Ex 1: 0. 87, -0. 81, 0. 43, 0. 07, -0. 98 0. 07, 0. 43, -0. 81, 0. 87, & -0. 98 Ex 2: 0. 32, -0. 65, 0. 63, -0. 42, 0. 04, 0. 32, -0. 42, 0. 63, & -0. 65
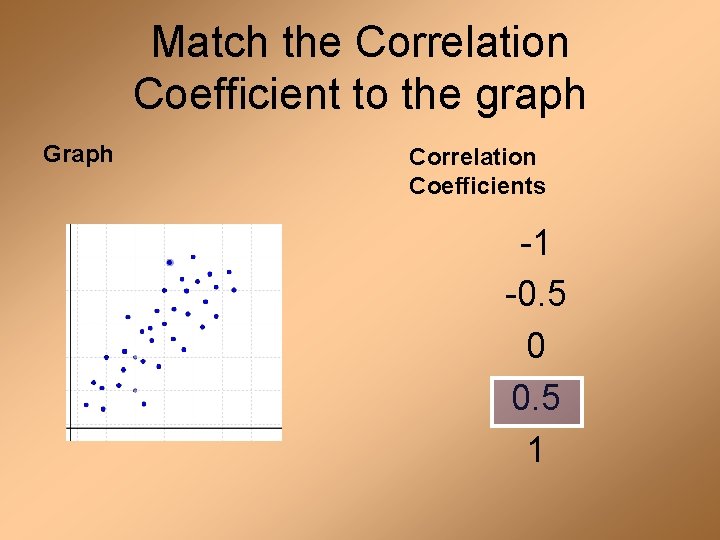
Match the Correlation Coefficient to the graph Graph Correlation Coefficients -1 -0. 5 0 0. 5 1
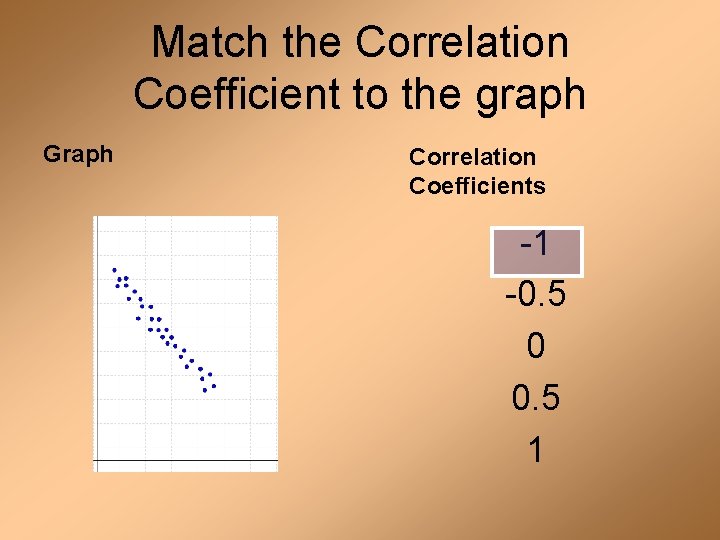
Match the Correlation Coefficient to the graph Graph Correlation Coefficients -1 -0. 5 0 0. 5 1
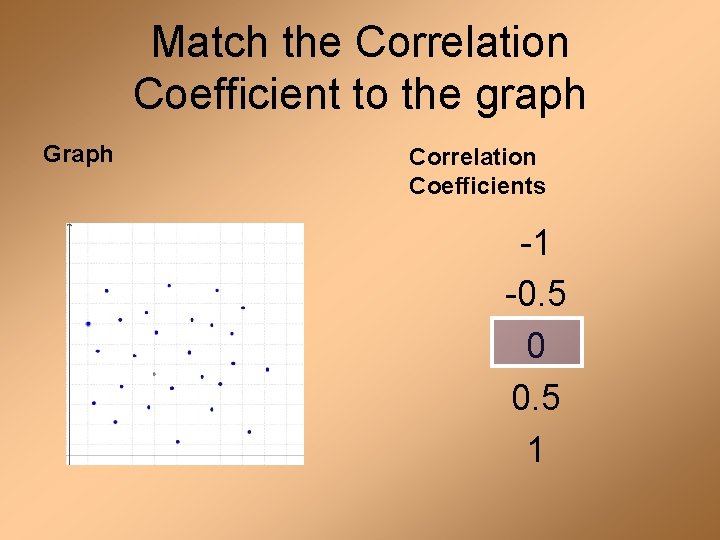
Match the Correlation Coefficient to the graph Graph Correlation Coefficients -1 -0. 5 0 0. 5 1

Positive, Negative, or No Correlation? A. The number of hours you work vs. The amount of money in your bank account Positive B. The number of hours workers receive safety training vs. The number of accidents on the job. Negative C. The number of students at Hillgrove vs. The number of dogs in Atlanta No Correlation

Some Types of Regression Linear Regression (straight line form) Quadratic Regression (parabolic form) Cubic Regression (cubic form)
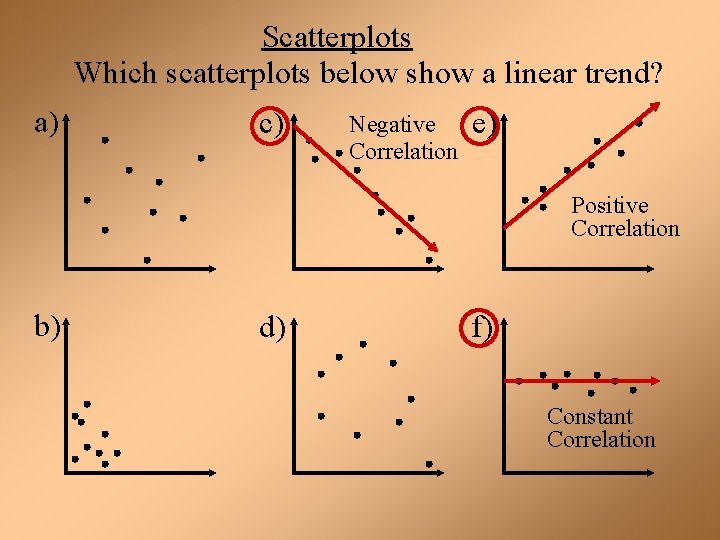
Scatterplots Which scatterplots below show a linear trend? a) c) Negative Correlation e) Positive Correlation b) d) f) Constant Correlation

Best Fit Line By Hand • The table shows the number of people y who attended each of the first seven football games x of the season. Approximate the best-fitting line for the data. • x 1 2 3 4 5 6 7 y • • 722 763 772 826 815 857 Steps: 1) Draw a scatter plot. 2) Sketch the best-fitting line. 3) Choose 2 data points on the best-fit line and solve for the slope. 4) Use one of the points and the slope to solve for b in y = mx + b. 897
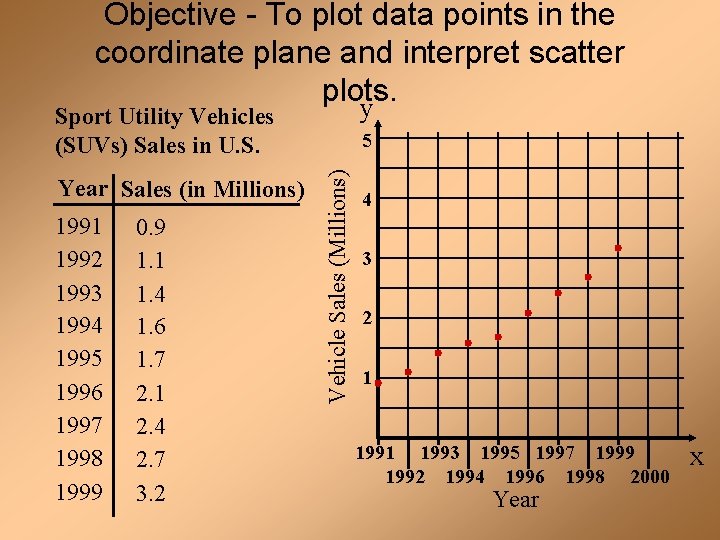
Objective - To plot data points in the coordinate plane and interpret scatter plots. y Sport Utility Vehicles (SUVs) Sales in U. S. 1991 1992 1993 1994 1995 1996 1997 1998 1999 0. 9 1. 1 1. 4 1. 6 1. 7 2. 1 2. 4 2. 7 3. 2 Vehicle Sales (Millions) Year Sales (in Millions) 5 4 3 2 1 1993 1995 1997 1999 1992 1994 1996 1998 2000 Year x
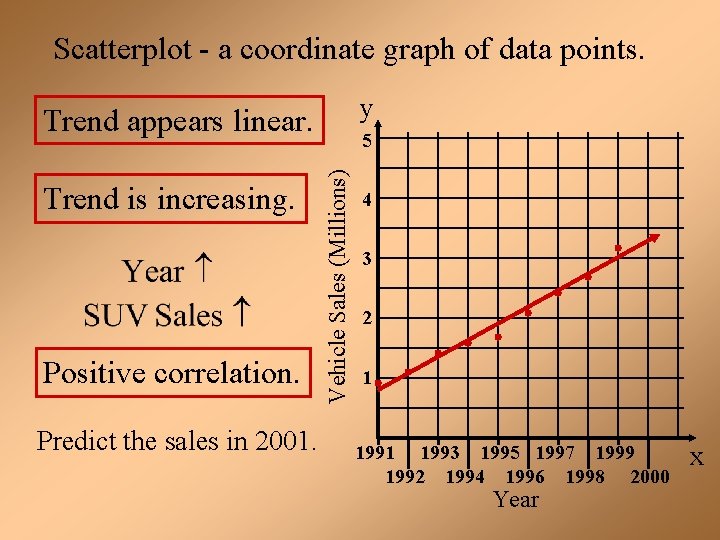
Scatterplot - a coordinate graph of data points. y Trend appears linear. Positive correlation. Predict the sales in 2001. Vehicle Sales (Millions) Trend is increasing. 5 4 3 2 1 1993 1995 1997 1999 1992 1994 1996 1998 2000 Year x

Plot the data on the graph such that homework time is on the y-axis and TV time is on the x-axis. . Time Spent Student Watching TV on Homework Sam 30 min. 180 min. Jon 45 min. 150 min. Lara 120 min. 90 min. Darren 240 min. 30 min. Megan 90 min. Pia 150 min. 90 min. Crystal 180 min. 90 min.
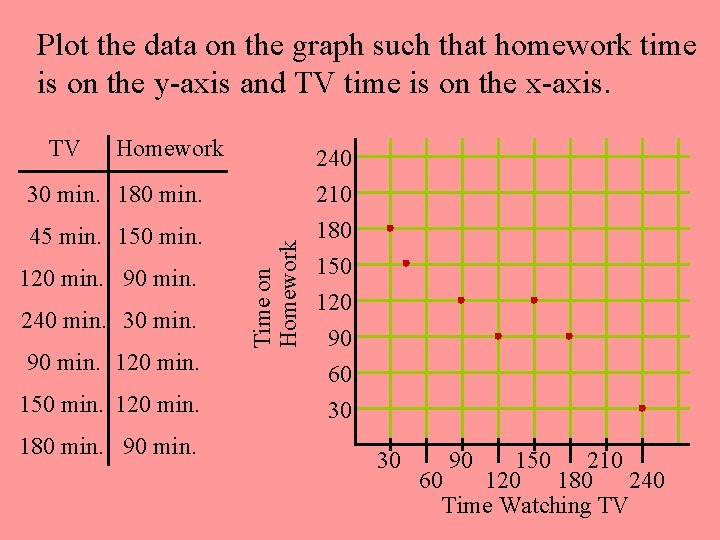
Plot the data on the graph such that homework time is on the y-axis and TV time is on the x-axis. TV Homework 240 45 min. 150 min. 120 min. 90 min. 240 min. 30 min. 90 min. 120 min. 150 min. 120 min. 180 min. 90 min. Time on Homework 30 min. 180 min. 210 180 150 120 90 60 30 30 90 150 210 60 120 180 240 Time Watching TV
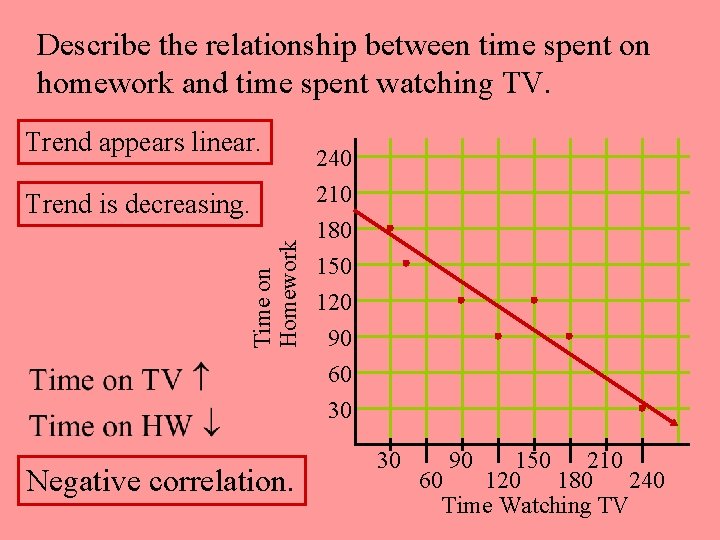
Describe the relationship between time spent on homework and time spent watching TV. Trend appears linear. Time on Homework Trend is decreasing. Negative correlation. 240 210 180 150 120 90 60 30 30 90 150 210 60 120 180 240 Time Watching TV
![Best Fit Line Using A TI-30 x Calculator 1) Press [2 nd], then [Stat] Best Fit Line Using A TI-30 x Calculator 1) Press [2 nd], then [Stat]](http://slidetodoc.com/presentation_image_h2/1fb685a4be96256c25ac5a5b08e72e16/image-25.jpg)
Best Fit Line Using A TI-30 x Calculator 1) Press [2 nd], then [Stat] 2) Select 2 -VAR 3) Press [Data] 4) X 1 = first data point’s x Y 1 = first data point’s y 5) Keep pressing down arrow to go to new points 6) Press [STATVAR] 7) a = slope, b = y-intercept

Best Fit Line Using A TI-84 Graphing Calculator • See Handout

Example 1: Consumer Debt The table shows the total outstanding consumer debt (excluding home mortgages) in billions of dollars in selected years. (Data is from the Federal Reserve Bulletin. ) Year 1985 1990 1995 2000 2003 Consumer Debt 585 789 1096 1693 1987 Let x = 0 correspond to 1985. a) Using a graphing calculator, draw the scatterplot. Interpret the plot: 1. Form 2. Strength 3. Direction

Example 1: Consumer Debt (cont) Year 1985 1990 1995 2000 2003 Consumer Debt 585 789 1096 1693 1987 b) Find the regression equation appropriate for this data set. Round values to two decimal places. c) Find and interpret the slope of the regression equation in the context of the scenario.

Example 1: Consumer Debt (cont) d) Find the approximate consumer debt in 1998. 1501. 52 billion e) Find the approximate consumer debt in 2008. 2300. 11 billion

Example 1: Consumer Debt (cont) f) Using the regression equation, predict the year when consumer debt will reach 2, 500 billion dollars. 25. 5 years or 2010 and a 1/2 year

Example 2: Health The table below shows the number of deaths per 100, 000 people from heart disease in selected years. (Data is from the U. S. National Center for Health Statistics. ) Year 1960 Deaths 559 1970 1980 1990 2002 483 412 322 258 240 Let x = 0 correspond to 1960. a) Using a graphing calculator, draw the scatterplot. Interpret the plot: 1. Form 2. Strength 3. Direction

Example 2: Health (cont) b) Find the regression equation appropriate for this data set. Round values to two decimal places. c) Find and interpret the slope of the regression equation in the context of the scenario.

Example 2: Health (cont) d) Find an approximation for the number of deaths due to heart disease in 1995. 635 e) Predict the number of deaths from heart disease in 2008. 194
- Slides: 33