Unit 3 The Modern Model of the Atom

Unit 3: The Modern Model of the Atom or The Quantum Mechanical (QM) Model or The Wave Model

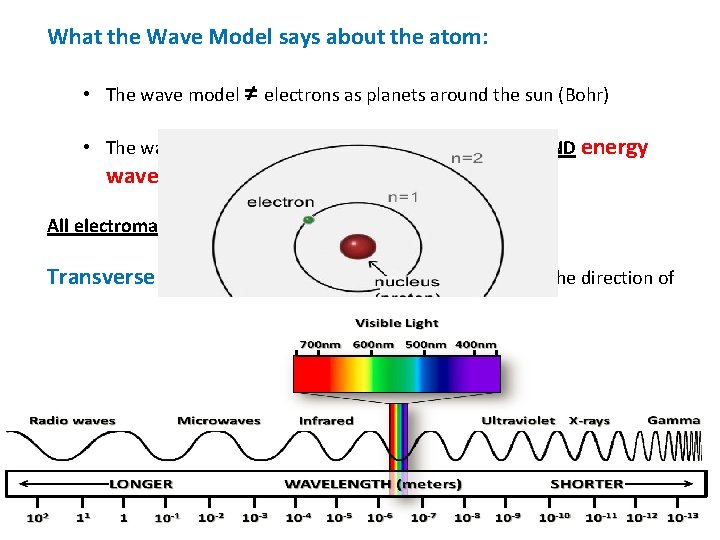
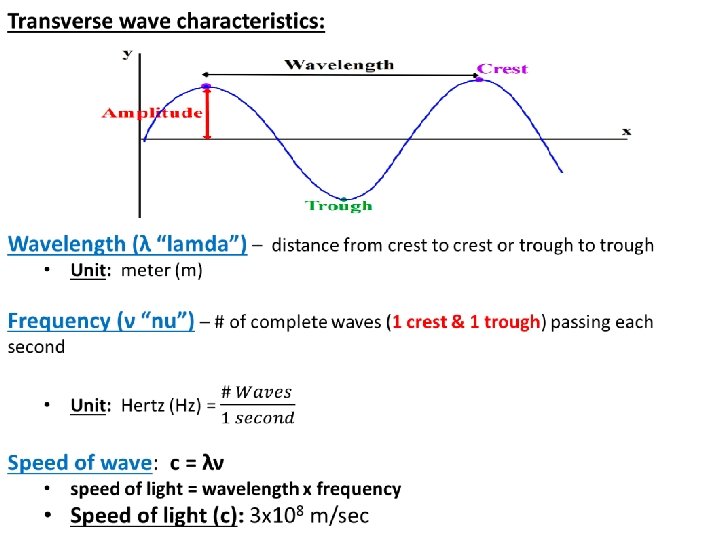
What the Wave Model says about the atom: • The wave model ≠ electrons as planets around the sun (Bohr) • The wave model = electrons as matter (particles) AND energy waves (electromagnetic radiation) All electromagnetic waves are: Transverse waves: motion of medium is at right angles to the direction of wave. Examples: light, heat, gamma, x-rays……. Medium – matter or region through which the wave travels Matter: “everything” – elements, compounds, mixtures Region: outer space – absence of matter

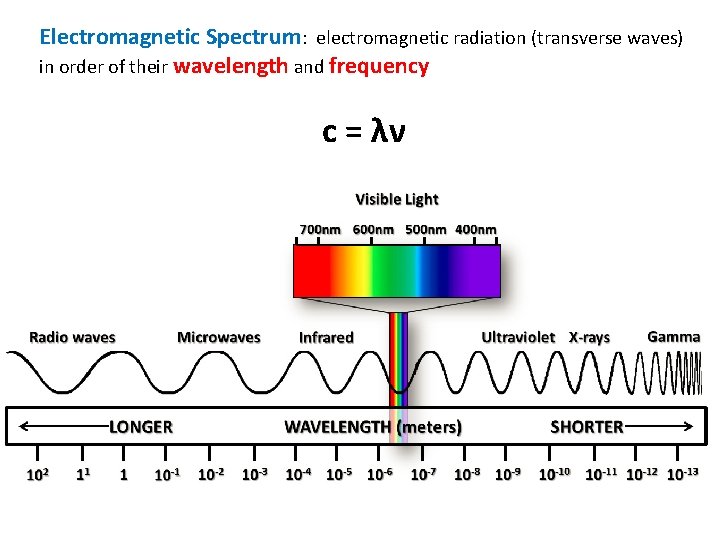
Electromagnetic Spectrum: electromagnetic radiation (transverse waves) in order of their wavelength and frequency c = λν

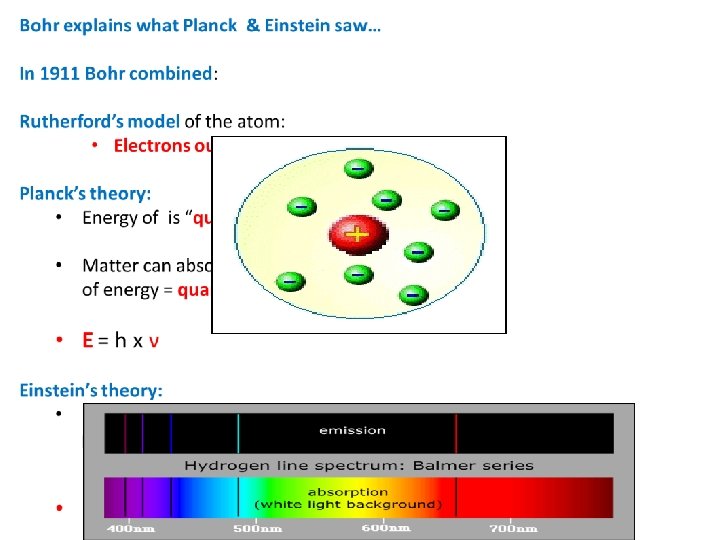
Planck & Einstein: Connect Matter & Energy Planck & “blackbody” radiation: • A “blackbody” is an object (matter) that can absorb all wavelengths of energy when heated. • In theory, the “blackbody” should be able to release an infinite number of wavelengths of energy. • Planck observed emission of only specific wavelengths! Planck Quantizes Energy: • Energy can be gained or lost only in discrete units called a “quantum”. E = hν Energy = Planck’s constant x frequency (nu) Planck’s constant (h) = 6. 626 X 10 -34 Joule seconds (J·s)

Evidence for the dual nature (wave & particle) of light: Light as wave: • Diffraction: the bending of light around a barrier. • Polarization: causing light waves to move only in one plane. Light as particle • Photoelectric effect: transfer of energy when photon impacts reactive surface.

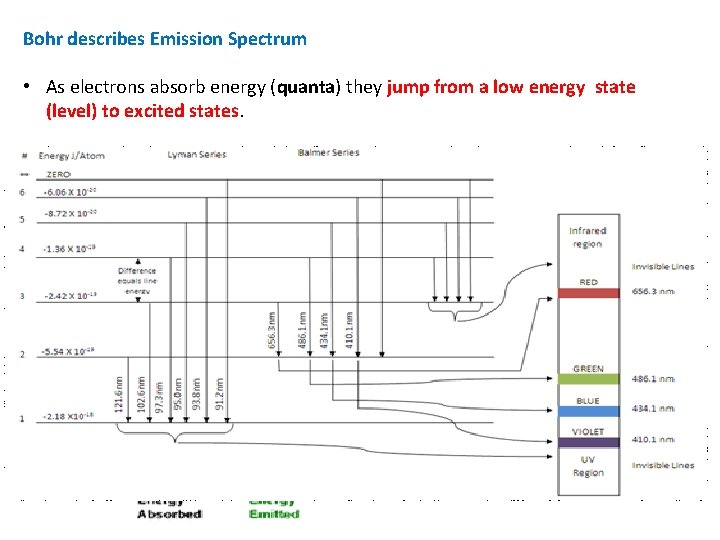
Evidence Part II Emission (line) Spectrum of Hydrogen yields more clues! Emission (line) spectrum : a spectrum that contains only certain colors or wavelengths of light (fingerprint of element) Continuous spectrum: a spectrum that contains all colors (sunlight or incandescent lights) Conclusion: line spectrum is produced because only certain energies are allowed for electron in Hydrogen atom. • Energy of electron is quantized!

The Bohr Model of the Atom • The Electron in a hydrogen atom moves around the nucleus only in allowed orbits (energy levels). • Each orbit (energy level) will be labeled by a quantum number (n) Quantum number: n= 1, 2, 3, 4, …… n = 1 Ground state / orbit closest to nucleus / lowest energy electron(s) n = 2, 3, 4, …. Excited states / becoming further from nucleus/ higher energy electron(s).

Bohr describes Emission Spectrum • As electrons absorb energy (quanta) they jump from a low energy state (level) to excited states. • Radiation (light) is given off when the electron “falls” from its excited state to a lower energy state. • The distance the electron “falls” corresponds to different colors in the spectrum and gives us spectral lines. ΔE = hν

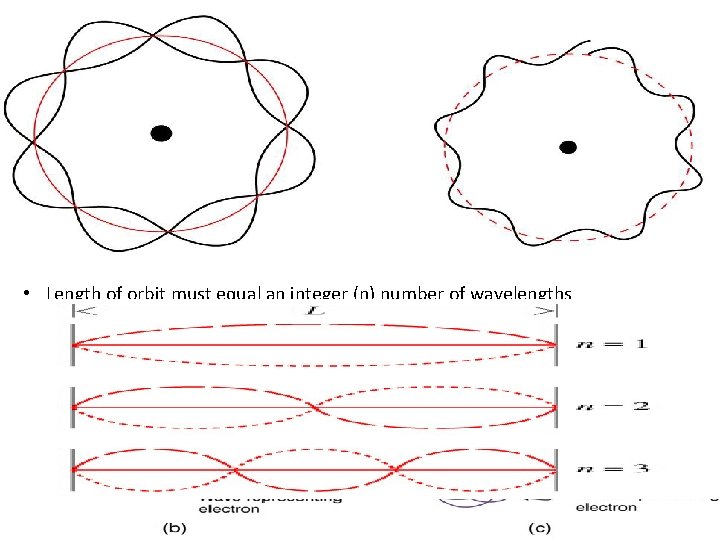
Why was Bohr’s model wrong? • Electrons in circular “orbits” would emit radiation (energy) and spiral into the protons in the nucleus! The Wave Model: Schrodinger & Heisenberg Schrodinger’s addition • Electrons as standing waves • Length of orbit must equal an integer (n) number of wavelengths • 2πr = n λ r= radius • Circumference (2πr ) of a circular orbit = whole number of wavelengths = certain electron energies

Schrodinger describes electron location (with math) • ĤΨ = EΨ • Ψ (psi) = Wave function (relates electron position in 3 -D space (x, y, z) • Ĥ = Operator (math that describes the energy of electron when applied to Ψ) • E = Energy of atom (sum of PE of electron/proton attraction & KE of electron) Many solutions are possible due to 3 -D space • Each solution consists of a wave function (Ψ) that is characterized by energy (E) • A wave function is called an ORBITAL • Orbitals describe the probable location of an electron Why probable? Let’s ask Heisenberg!

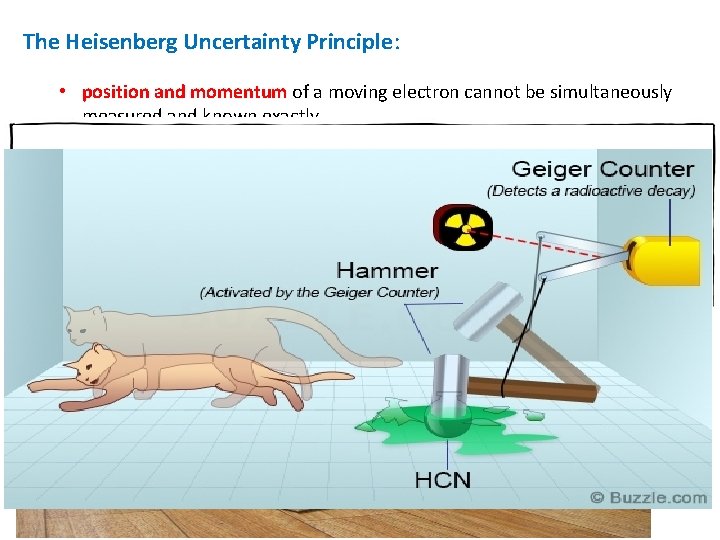
The Heisenberg Uncertainty Principle: • position and momentum of a moving electron cannot be simultaneously measured and known exactly. Schrodinger’s Cat