Unit 3 Section 3 Logic Intro to Proofs

Unit 3 Section 3 Logic: Intro to Proofs

If we want to prove a conditional statement is true, we antecedent and step-by-step, we show start with the _____ consequent that the ______ is true. At each step we have justify our conclusion to _________. The justification is something that is true, like o Properties o h Definitions o H Postulates o h Theorems

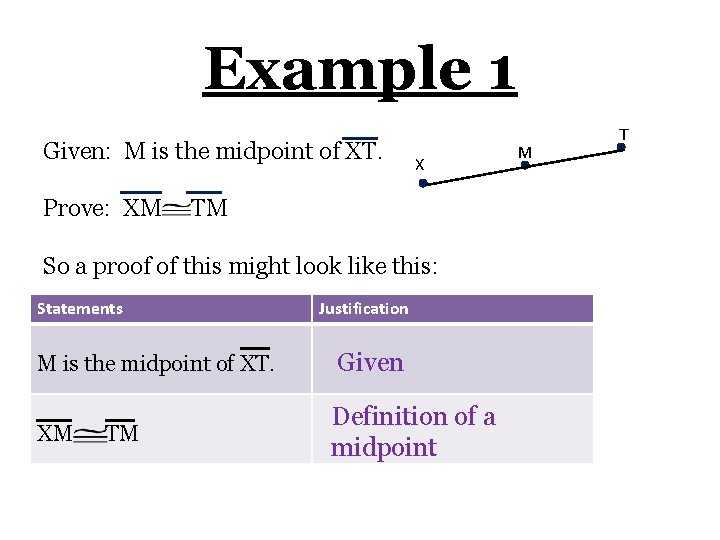
Example 1 Given: M is the midpoint of XT. Prove: XM X M T TM Think of this as a conditional statement, with the given as the antecedent and what you want to prove as the consequent: ________________. If M is the midpoint, then XM TM Where have you seen this before? This is one direction of the ___________. definition of the midpoint

Example 1 Given: M is the midpoint of XT. Prove: XM X TM So a proof of this might look like this: Statements Justification M is the midpoint of XT. Given XM Definition of a midpoint TM M T

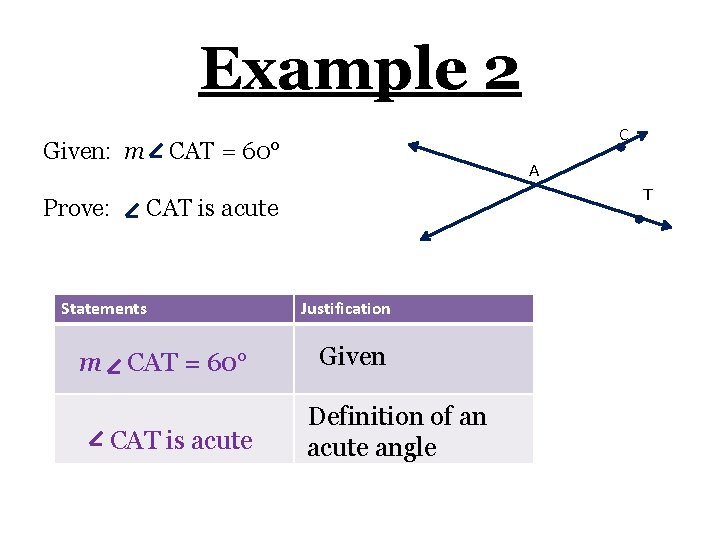
Example 2 C Given: m CAT = 60° Prove: A T CAT is acute Statements m CAT = 60° CAT is acute Justification Given Definition of an acute angle

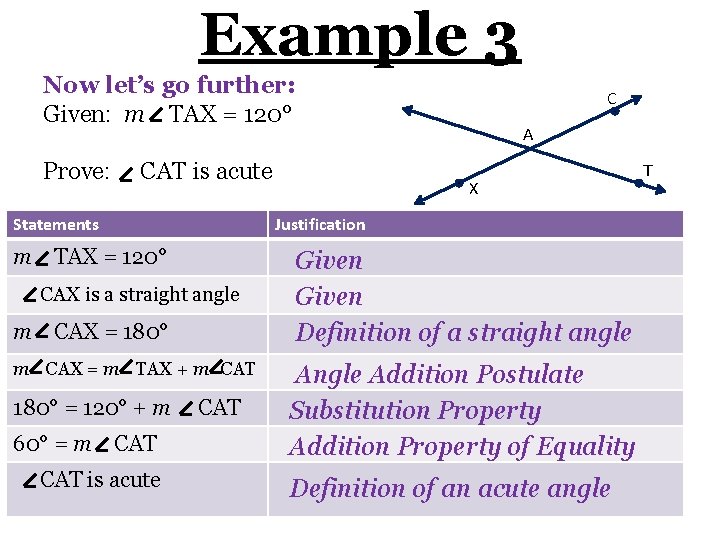
Example 3 Now let’s go further: Given: m TAX = 120° Prove: CAT is acute Statements CAX is a straight angle m CAX = 180° m CAX = m TAX + m CAT 60° = m CAT is acute A X Justification m TAX = 120° 180° = 120° + m C CAT Given Definition of a straight angle Addition Postulate Substitution Property Addition Property of Equality Definition of an acute angle T

You were already doing problems like finding the measure of CAT, without realizing how many steps you were thinking through as you did them! proofs is to break down the thinking The trick to doing _____ and to make sure that each step is a logical conclusion of things you already have written down. Now let’s prove our first theorem – something we have already observed in angle problems we’ve done. The Vertical Angles Congruence Theorem says “If two angles are vertical, then they are congruent. ” To prove this, we assume that the ________. antecedent is true That is we have a _________. We try to prove they are vertical angle pair congruent.

Example 4 Given: 2 and 4 are vertical angles 1 4 Prove: 2 4 Statements 2 & 4 are vertical angles 1 + 2 = 180° 1 + 4 = 180° 1+ 2= 1+ 4 2= 4 2 4 3 2 Justification Given Linear Pairs are supplementary Substitution Property Addition Property of Equality Definition of Congruence