Unit 3 Rational Numbers Math 9 November Types

Unit 3 – Rational Numbers Math 9 - November

Types of Numbers You will want to copy these definitions for reference. �Natural Numbers � 1, 2, 3, 4…… �Rational Numbers � a/b when b is not 0 �Whole Numbers �Irrational Numbers � 0, 1, 2, 3, 4…… � Cannot be a/b �Integers � …. -3, -2, -1, 0, 1, 2, 3…. . �Real Numbers � Rational + Irrational #s

What Temperature? �The label on a package of frozen cranberries says that it must be stored at temperatures between -18 C and 22 C. What are some possible temperatures it can be stored at? �Record a temperature between -18 C and -22 C on your sticky.

3. 1 – What is a Rational Number? �What is an integer?

3. 1 – What is a Rational Number? Integers – a set of numbers that include positive and negative numbers AND zero Represented by - I

3. 1 – What is a Rational Number? �What is a rational number? -1 0 1

3. 1 – What is a Rational Number? �Any number that can be written as a fraction with an integer numerator and a non-zero integer denominator is a Rational Number.

3. 1 – What is a Rational Number? �Any number that can be written as a fraction with an integer numerator and a non-zero integer denominator is a Rational Number. �Rational Numbers are represented as Q �Rational Numbers include all integers, fractions, terminating decimals and repeating decimals

$3. 1 What is a Rational Number �Using integers you can create a fraction$

3. 1 What is a Rational Number �Using integers you can create a fraction (a rational number) and then you can change it to a decimal � A) -6/3 � B) 2/3 � C) 7/8 � D) 100/25

3. 1 – What is a Rational Number? �When a number can NOT be written as a fraction it is not a rational number �What is it?

3. 1 – What is a Rational Number? �When a number can NOT be written as a fraction it is not a rational number �What is it? – Irrational Number �Irrational Numbers are all non-repeating and non- terminating decimals. They are represented by a Q with a hat

3. 1 – What is a Rational Number? �Identify the rational numbers below:

3. 1 – What is a Rational Number? �Draw a number line showing -5, 0 and 5

3. 1 – What is a Rational Number? � Draw a number line showing -5, 0 and 5 � Put the following rational numbers on your number line: �-2. 09 � 1. 2 �-3. 99 �-12/9 � 24/5

3. 1 B – Ordering Rational Numbers �Identify a decimal between each pair of rational numbers:

$3. 1 B – Ordering Rational Numbers �Identify a fraction between each pair of$

3. 1 B – Ordering Rational Numbers �Identify a fraction between each pair of rational numbers:

3. 1 – Ordering Rational Numbers �Math Practice Pages 101 - 103 �Questions – 5, 6, 7, 8, 10, 15, 17, 20 �Remember – no calculators

3. 1 B – Ordering Rational Numbers �My favourite NO! �Place the following numbers in descending order:

Rational Numbers – What you’ll learn �How to: �Identify positive and negative decimals and fractions as rational numbers �Compare and order rational numbers �Add, subtract, multiply and divide rational numbers �Solve problems that involve rational numbers �Apply the order of operations with rational numbers

3. 2 – Adding Rational Numbers (Integers)

$3. 2 – Adding Rational Numbers (fractions)$

3. 2 – Adding Rational Numbers (fractions)

3. 2 Adding Rational Numbers

3. 2 – Adding Rational Numbers

3. 2 Adding Rational Numbers

$3. 2 Adding Fractions �Change mixed fractions to improper fractions �Find common dominators first$

3. 2 Adding Fractions �Change mixed fractions to improper fractions �Find common dominators first (make the bottom # the same) �Show your answer in lowest terms

3. 2 Adding Fractions �Try these – remember, always give your answer in proper format

3. 2 – Adding Integers �Quick Practice

3. 2 – Adding Rational Numbers �Math Practice �Page 111 � Questions – 3, 4, 5, 6, 7, 8, 11 and 12

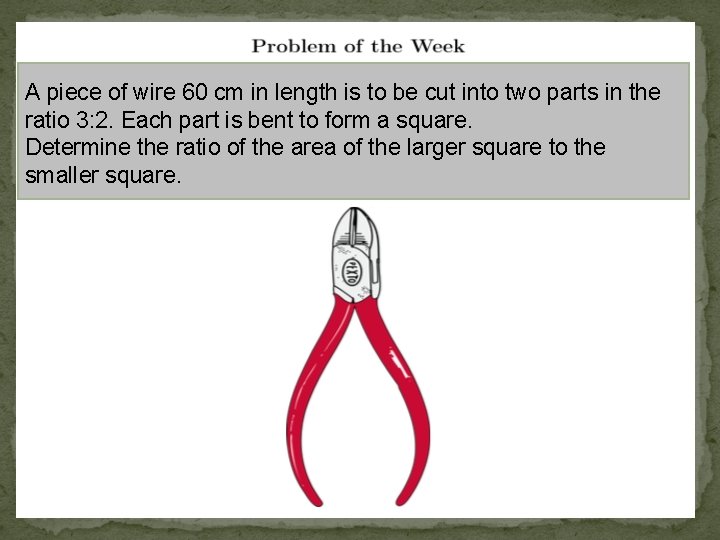
A piece of wire 60 cm in length is to be cut into two parts in the ratio 3: 2. Each part is bent to form a square. Determine the ratio of the area of the larger square to the smaller square.

3. 3 Subtracting Rational Numbers

3. 3 Subtracting Rational Numbers �Math Practice Pages 119 - 120 �Questions – 3 cd, 5 cd, 7 def, 8, 9 def, 10, 11, 13 cd, 14 cd, 15

3. 4 Multiplying Rational Numbers

3. 4 Multiplying Rational Numbers When multiplying or dividing rational numbers, the rules for the positive and negative signs are the same as with integers.

$3. 4 Multiplying Rational Numbers �To multiply fractions, multiply straight across (no tricks). �If$

3. 4 Multiplying Rational Numbers �To multiply fractions, multiply straight across (no tricks). �If you are dealing with a negative sign, keep it with the numerator.

3. 4 Multiplying Rational Numbers

3. 4 Multiplying Rational Numbers Try multiplying and then reduce to simplest terms.

3. 4 Multiplying Rational Numbers �It would be easier to reduce first before multiplying such big numbers. Fraction TRICK! �Because we are multiplying, you can reduce either numerator with either denominator.

3. 4 Multiplying Rational Numbers

3. 4 Multiplying Rational Numbers �To multiply decimals (WITHOUT a calculator!!!) line up the last decimal place. Put the number with the most digits on top. A. (-1. 5) x 1. 8 = ? ? ? B. (-2. 6) x (-3. 25) = ? ? ?

3. 4 Multiplying Rational Numbers

3. 4 Multiplying Rational Numbers �How would you complete this question? Work it out in your notebook or binder and show me before going on to the practice questions. �Practice Page 127 in Math Makes Sense � Questions – 3 cd, 4 cd, 6, 7, 8, 9, 10, 11 cd, 12 cd, 13, 14, 15

3. 5 Dividing Rational Numbers �Remember grade 4 division examples -> you have 15 candies and 5 friends, how many candies do they get…. .

3. 5 Dividing Rational Numbers �Dividing decimals – aren’t you glad we reviewed division last week �Solve each of the following without using your calculator:

3. 5 Dividing Rational Numbers

3. 5 Dividing Rational Numbers �So that was dividing a decimal by an integer. �What if we divide a decimal by a decimal?

3. 5 Dividing Rational Numbers

3. 5 Dividing Rational Numbers �Dividing Fractions

3. 5 Dividing Rational Numbers �Try a few:

3. 5 Dividing Rational Numbers �Work out the following questions, come show me your answers and then work on math practice: A)) B)) C)) �Practice – Page 134 � Questions 3(cdef), 4 (ef), 6, 8, 9 (de), 10, 11, 12 (cdef), 13, 14, 15, 17 (cd), 18 (cd) and 19 � QUIZ on Topics 3. 1 – 3. 5 on Wednesday next week.

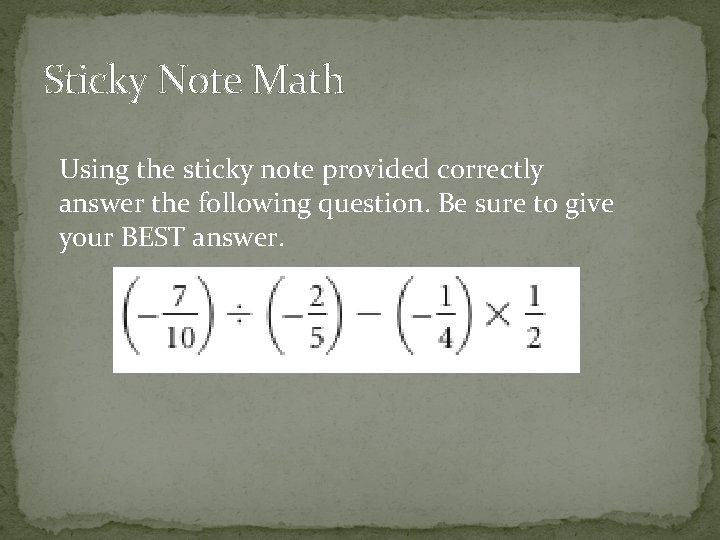
Sticky Note Math Using the sticky note provided correctly answer the following question. Be sure to give your BEST answer.

Rational Rules to Remember! �Addition �Subtraction �Multiplication �Division

Rational Rules to Remember! �Addition � When adding positive numbers move right � When adding negative numbers move left � Line up decimals � Use common denominators with fractions Always – DOES IT MAKE SENSE? ?

Rational Rules to Remember! �Subtraction � When subtracting positive numbers move left � When subtracting negative numbers move right � When subtracting a negative – boink! � With decimals – consider integers first! � Use common denominators with fractions Always – DOES IT MAKE SENSE? ?

Rational Rules to Remember! �Multiplication � Use integer rules for +/- signs � Fractions - Multiply straight across (no tricks)! �Change mixed fractions to improper first �Reduce early whenever possible � Decimals – Line them up �Most digits on top �Decimals in Q are in A Always – DOES IT MAKE SENSE? ?

Rational Rules to Remember! �Division � Use integer rules for +/- signs � Fractions – You can NOT straight divide �Multiply the reciprocal � Decimals – PRACTICE �Consider your decimal places Always – DOES IT MAKE SENSE? ?

3. 6. Order of Operations & Rational Numbers

3. 6. Order of Operations & Rational Numbers Work out the following questions, come show me your answers and then work on math practice: Page 140 Questions: 3(cd) 4(cd) 7 (cd) 8, 9, 10, 11, 12(cd), 13, 14, 15, 16, 17 Challenge Page 143 Questions – 19 -21

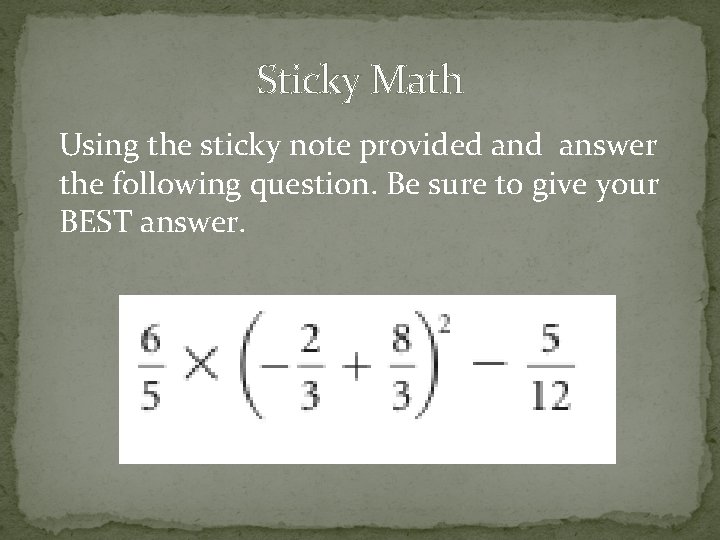
Sticky Math Using the sticky note provided answer the following question. Be sure to give your BEST answer.

Rational Numbers Review �Page 144 – 145 �Questions – Do ALL questions 1 -23 but only do as many sub questions (a/b/c’s) as you need. �Take a look at the study guide on page 143 �Review the challenge questions we worked on in December

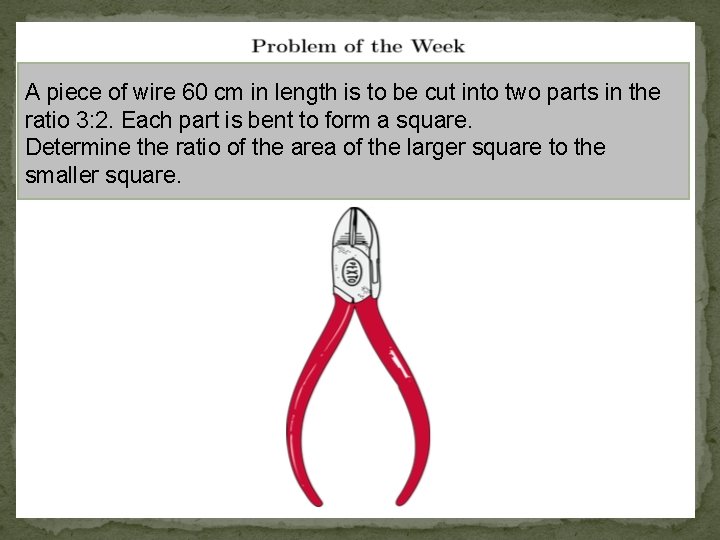
A piece of wire 60 cm in length is to be cut into two parts in the ratio 3: 2. Each part is bent to form a square. Determine the ratio of the area of the larger square to the smaller square.