Unit 3 Nonlinear Data Structure Tree Part 3

Unit – 3 Nonlinear Data Structure Tree – Part 3 Balanced Tree (Height / Weight Balanced) Multiway Search Tree (B-Tree) Prof. Pradyumansinh Jadeja � 9879461848 �pradyuman. jadeja@darshan. ac. in Data Structure (2130702) Darshan Institute of Engineering & Technology

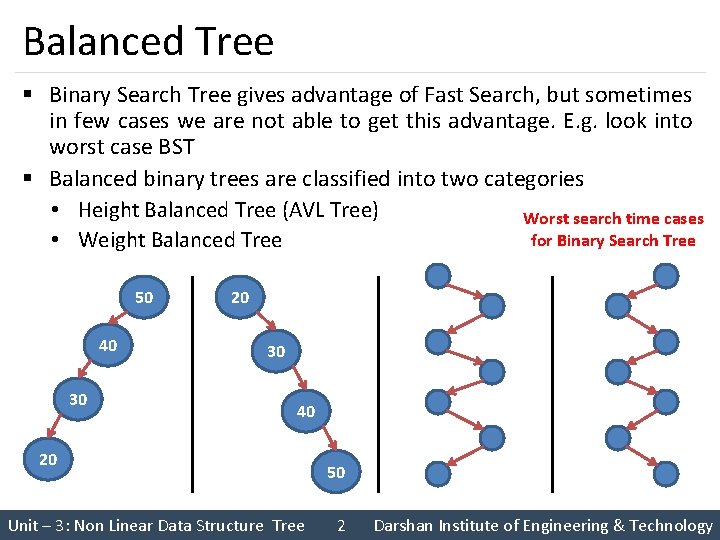
Balanced Tree § Binary Search Tree gives advantage of Fast Search, but sometimes in few cases we are not able to get this advantage. E. g. look into worst case BST § Balanced binary trees are classified into two categories • Height Balanced Tree (AVL Tree) Worst search time cases for Binary Search Tree • Weight Balanced Tree 50 40 30 20 30 40 20 Unit – 3: Non Linear Data Structure Tree 50 2 Darshan Institute of Engineering & Technology

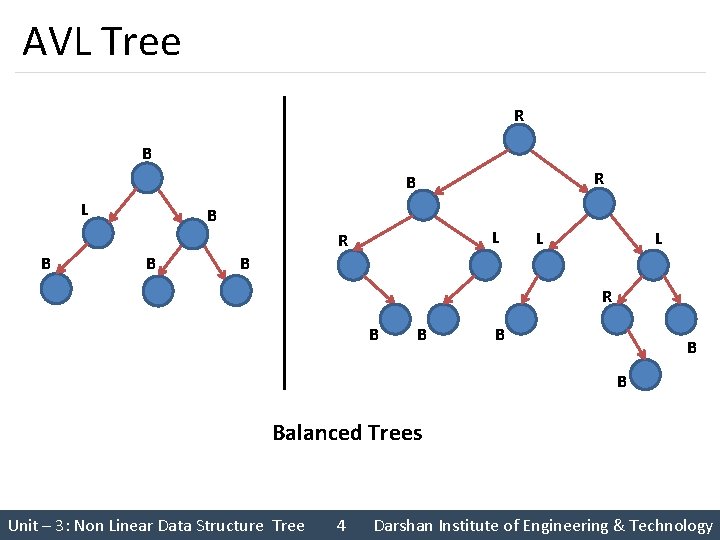
Height Balanced Tree (AVL Tree) § A tree is called AVL tree (Height Balanced Tree), if each node possessed one of the following properties • A node is called left heavy, if the longest path in its left sub tree is one longer than the longest path of its right sub tree • A node is called right heavy, if the longest path in its right subtree is one longer than the longest path of its left sub tree • A node is called balanced, if the longest path in both the right and left sub-trees are equal § In height balanced tree, each node must be in one of these states § If there exists a node in a tree where this is not true, then such a tree is called Unbalanced Unit – 3: Non Linear Data Structure Tree 3 Darshan Institute of Engineering & Technology

AVL Tree R B L B L R B B L L B R B B Balanced Trees Unit – 3: Non Linear Data Structure Tree 4 Darshan Institute of Engineering & Technology

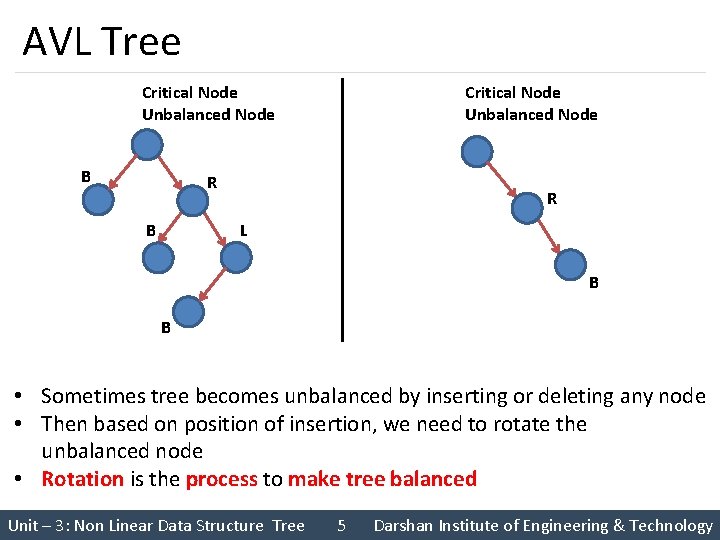
AVL Tree Critical Node Unbalanced Node B Critical Node Unbalanced Node R B R L B B • Sometimes tree becomes unbalanced by inserting or deleting any node • Then based on position of insertion, we need to rotate the unbalanced node • Rotation is the process to make tree balanced Unit – 3: Non Linear Data Structure Tree 5 Darshan Institute of Engineering & Technology

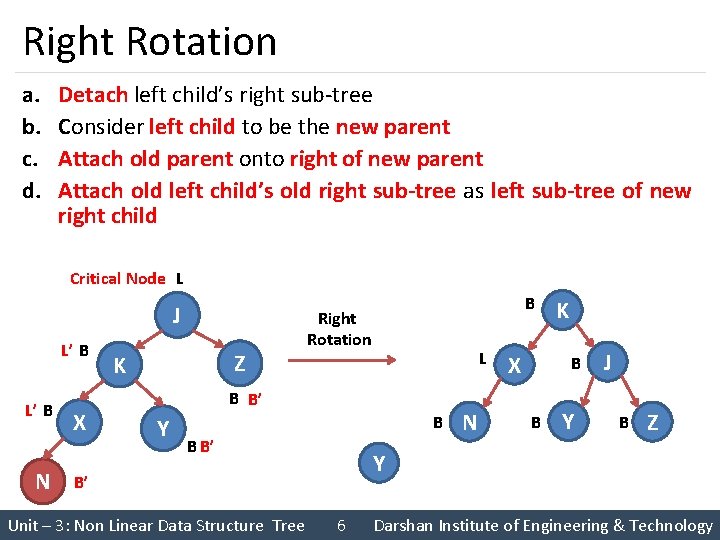
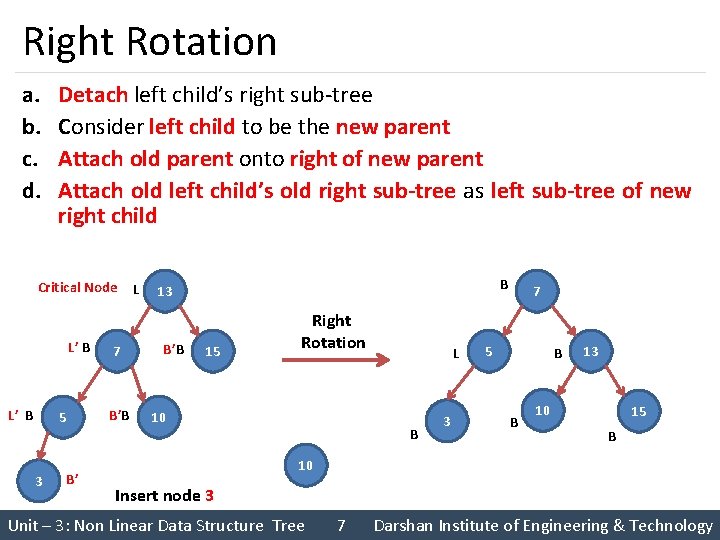
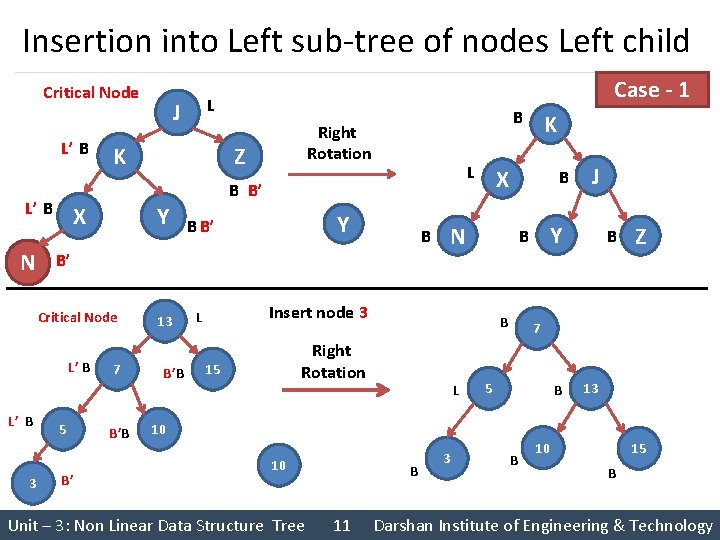
Right Rotation a. b. c. d. Detach left child’s right sub-tree Consider left child to be the new parent Attach old parent onto right of new parent Attach old left child’s old right sub-tree as left sub-tree of new right child Critical Node L J L’ B N X Z K B Right Rotation L B B’ Y B B B’ B B Y J B Z Y B’ Unit – 3: Non Linear Data Structure Tree N X K 6 Darshan Institute of Engineering & Technology

Right Rotation a. b. c. d. Detach left child’s right sub-tree Consider left child to be the new parent Attach old parent onto right of new parent Attach old left child’s old right sub-tree as left sub-tree of new right child Critical Node L’ B 5 3 B’ 7 B’B L B 13 B’ B 15 Right Rotation 10 L B 3 7 5 B B 13 10 15 B 10 Insert node 3 Unit – 3: Non Linear Data Structure Tree 7 Darshan Institute of Engineering & Technology

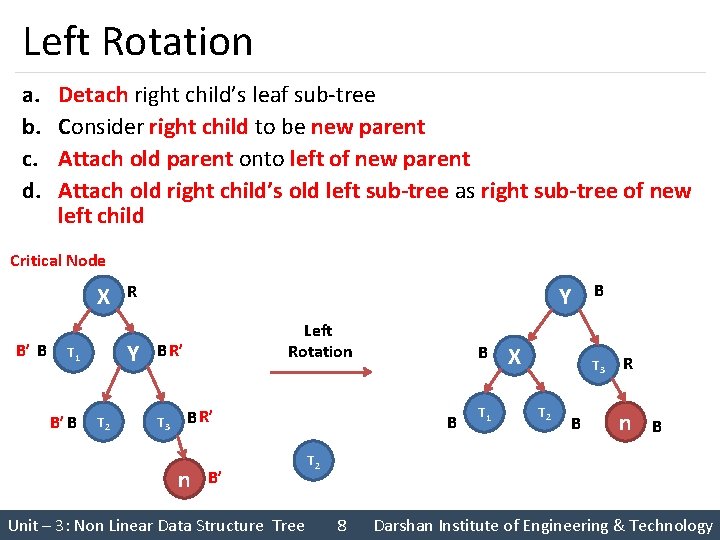
Left Rotation a. b. c. d. Detach right child’s leaf sub-tree Consider right child to be new parent Attach old parent onto left of new parent Attach old right child’s old left sub-tree as right sub-tree of new left child Critical Node X B’ B Y T 1 B’ B R T 2 Y Left Rotation B R’ T 3 B R’ n B’ Unit – 3: Non Linear Data Structure Tree B B T 1 X B T 3 T 2 B R n B T 2 8 Darshan Institute of Engineering & Technology

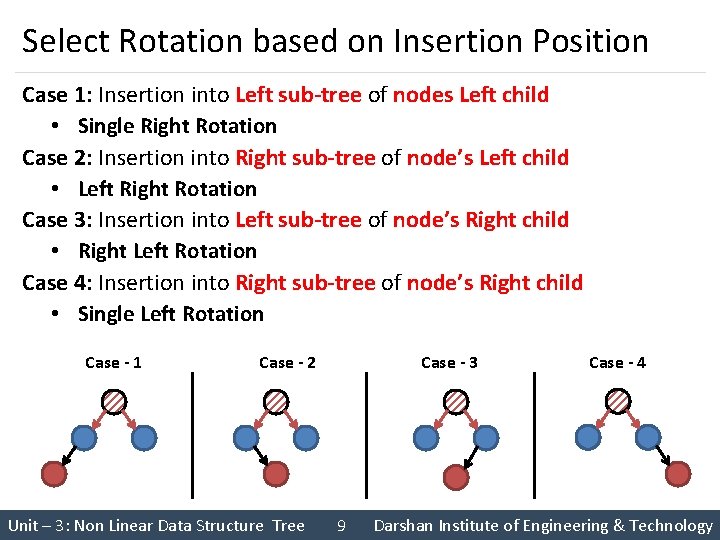
Select Rotation based on Insertion Position Case 1: Insertion into Left sub-tree of nodes Left child • Single Right Rotation Case 2: Insertion into Right sub-tree of node’s Left child • Left Right Rotation Case 3: Insertion into Left sub-tree of node’s Right child • Right Left Rotation Case 4: Insertion into Right sub-tree of node’s Right child • Single Left Rotation Case - 1 Case - 2 Unit – 3: Non Linear Data Structure Tree Case - 3 9 Case - 4 Darshan Institute of Engineering & Technology

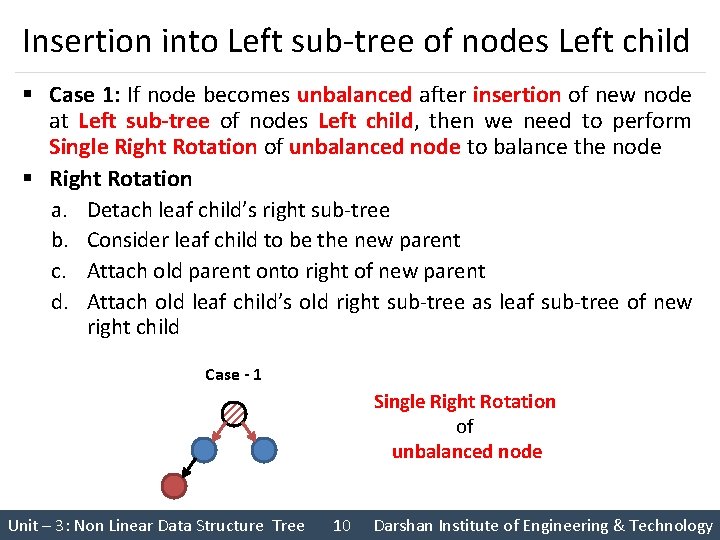
Insertion into Left sub-tree of nodes Left child § Case 1: If node becomes unbalanced after insertion of new node at Left sub-tree of nodes Left child, then we need to perform Single Right Rotation of unbalanced node to balance the node § Right Rotation a. Detach leaf child’s right sub-tree b. Consider leaf child to be the new parent c. Attach old parent onto right of new parent d. Attach old leaf child’s old right sub-tree as leaf sub-tree of new right child Case - 1 Single Right Rotation of unbalanced node Unit – 3: Non Linear Data Structure Tree 10 Darshan Institute of Engineering & Technology

Insertion into Left sub-tree of nodes Left child Critical Node L’ B 3 K B Right Rotation Z X Y B B’ L Critical Node 13 L Y B B’ L’ B J B B’ L’ B N Case - 1 L 5 B’ 7 B’B B’ B X B L J Y B Insert node 3 15 B N Right Rotation K B Z 7 5 B 13 10 10 Unit – 3: Non Linear Data Structure Tree B 11 3 B 10 15 B Darshan Institute of Engineering & Technology

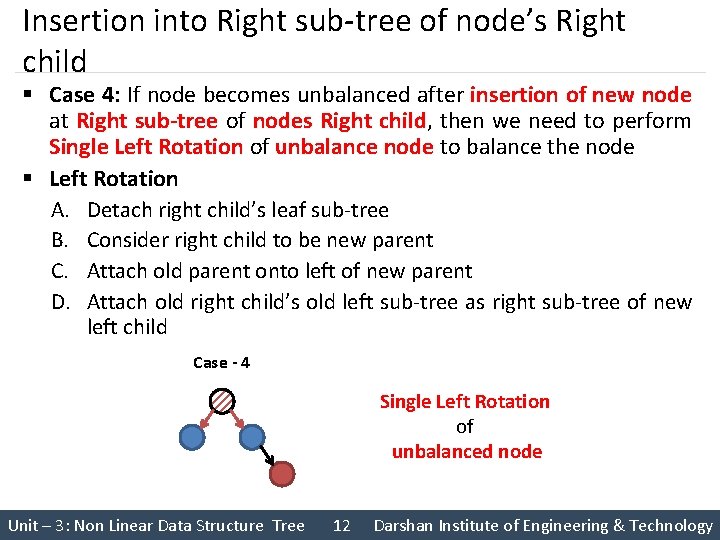
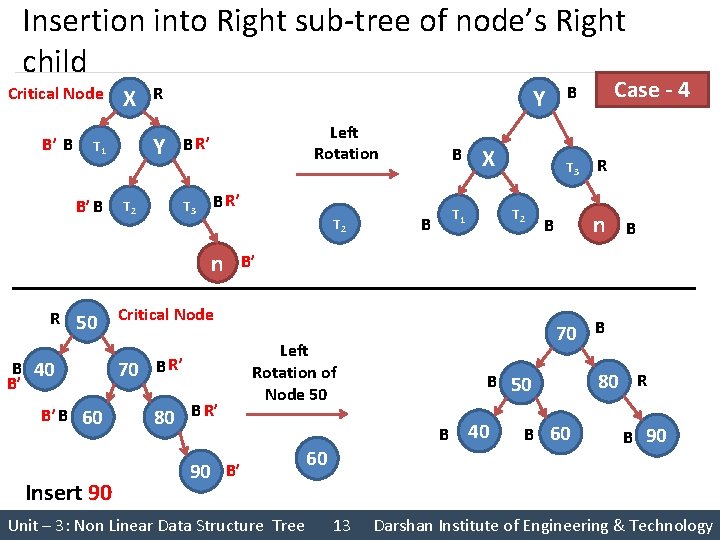
Insertion into Right sub-tree of node’s Right child § Case 4: If node becomes unbalanced after insertion of new node at Right sub-tree of nodes Right child, then we need to perform Single Left Rotation of unbalance node to balance the node § Left Rotation A. Detach right child’s leaf sub-tree B. Consider right child to be new parent C. Attach old parent onto left of new parent D. Attach old right child’s old left sub-tree as right sub-tree of new left child Case - 4 Single Left Rotation of unbalanced node Unit – 3: Non Linear Data Structure Tree 12 Darshan Institute of Engineering & Technology

Insertion into Right sub-tree of node’s Right child Critical Node B’ B X Y T 1 B’ B R Y Left Rotation B R’ T 3 T 2 B R’ T 2 n R 50 B 40 B’ B’ B 60 Insert 90 B X T 3 T 2 T 1 B 80 B R’ R n B B B’ Critical Node 70 B R’ Case - 4 B 70 B Left Rotation of Node 50 90 B’ Unit – 3: Non Linear Data Structure Tree B 50 B 60 13 40 B 60 80 R B 90 Darshan Institute of Engineering & Technology

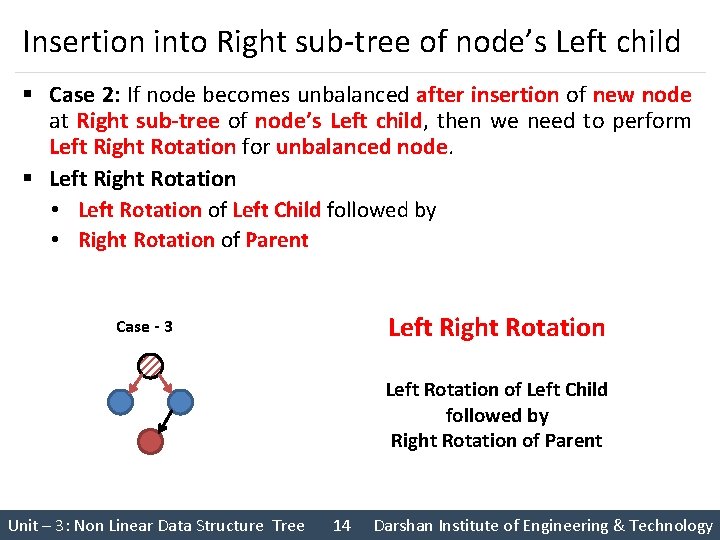
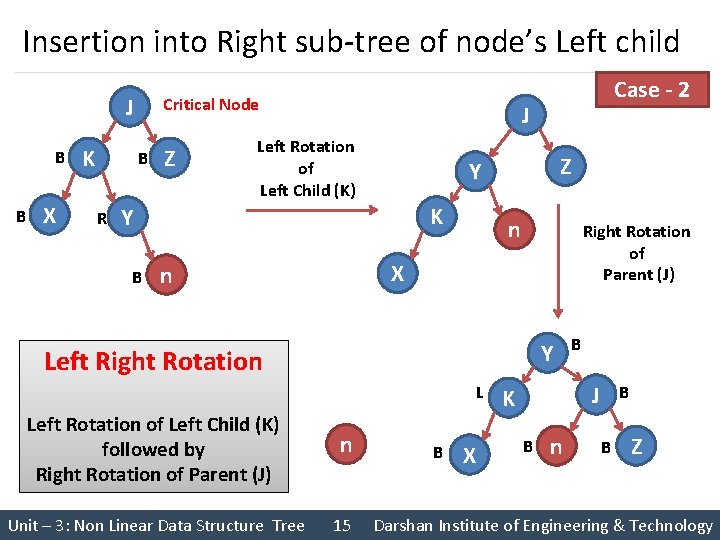
Insertion into Right sub-tree of node’s Left child § Case 2: If node becomes unbalanced after insertion of new node at Right sub-tree of node’s Left child, then we need to perform Left Right Rotation for unbalanced node. § Left Right Rotation • Left Rotation of Left Child followed by • Right Rotation of Parent Left Right Rotation Case - 3 Left Rotation of Left Child followed by Right Rotation of Parent Unit – 3: Non Linear Data Structure Tree 14 Darshan Institute of Engineering & Technology

Insertion into Right sub-tree of node’s Left child J B B X K Critical Node B R Z J Left Rotation of Left Child (K) Z Y K Y B Case - 2 n Right Rotation of Parent (J) X n Y Left Right Rotation L Left Rotation of Left Child (K) followed by Right Rotation of Parent (J) n Unit – 3: Non Linear Data Structure Tree 15 B X B J K B n B B Z Darshan Institute of Engineering & Technology

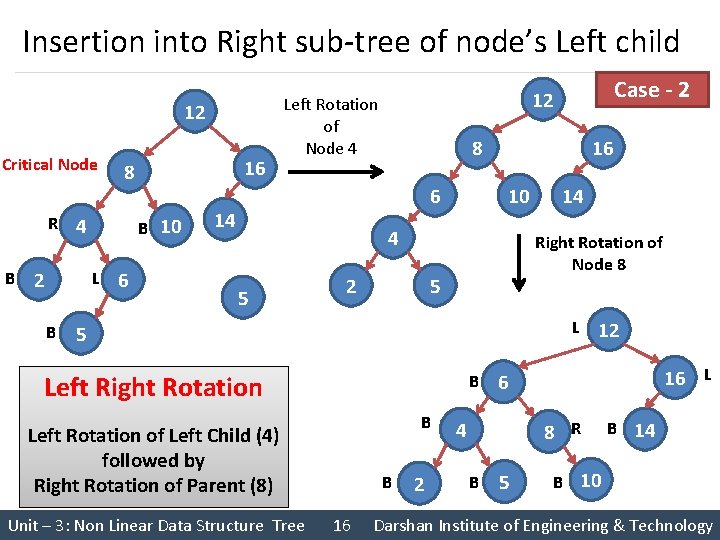
Insertion into Right sub-tree of node’s Left child 12 Critical Node R B 4 2 B 10 L B 16 8 6 14 16 10 4 5 2 14 Right Rotation of Node 8 5 Left Right Rotation B B Left Rotation of Left Child (4) followed by Right Rotation of Parent (8) Unit – 3: Non Linear Data Structure Tree Case - 2 12 Left Rotation of Node 4 B 16 2 12 16 L 6 4 8 R B 5 B 14 B 10 Darshan Institute of Engineering & Technology

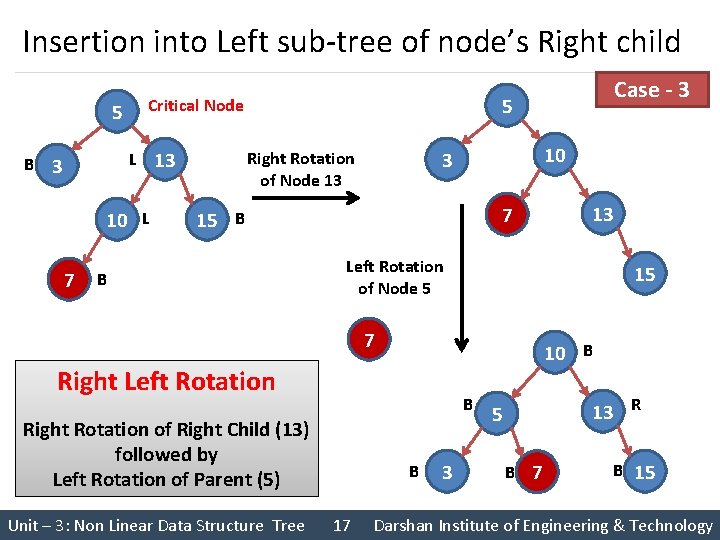
Insertion into Left sub-tree of node’s Right child 5 B L 3 10 L 7 13 Case - 3 5 Critical Node 10 3 Right Rotation of Node 13 7 15 B B Left Rotation of Node 5 15 7 10 B Right Left Rotation B Right Rotation of Right Child (13) followed by Left Rotation of Parent (5) Unit – 3: Non Linear Data Structure Tree 13 B 17 3 13 R 5 B 7 B 15 Darshan Institute of Engineering & Technology

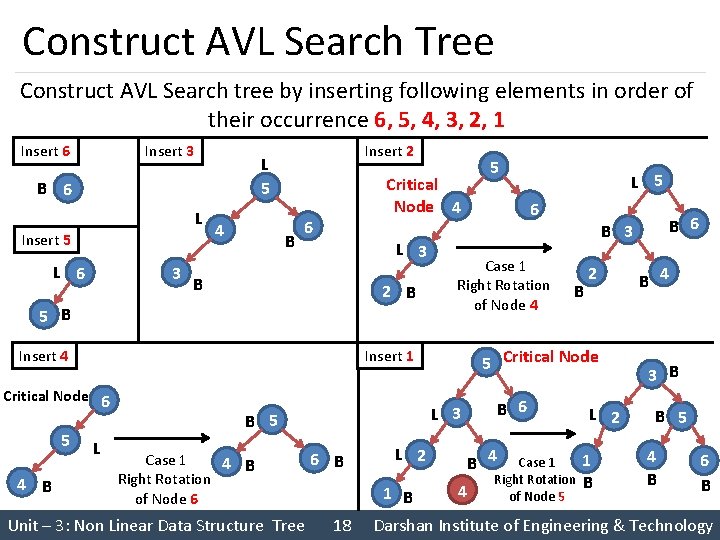
Construct AVL Search Tree Construct AVL Search tree by inserting following elements in order of their occurrence 6, 5, 4, 3, 2, 1 Insert 6 Insert 3 B 6 L Insert 5 L 6 3 Insert 2 L 5 4 B Critical Node 4 6 L 3 B 2 B 5 B Insert 4 5 4 B L Case 1 4 B Right Rotation of Node 6 Unit – 3: Non Linear Data Structure Tree 6 B 2 L 2 1 B 18 6 B B 6 B 4 4 B 6 B 3 2 5 Critical Node L 3 B 5 L 5 Case 1 Right Rotation of Node 4 Insert 1 Critical Node 6 5 Case 1 Right Rotation of Node 5 L 2 1 B B 4 3 B B 5 4 B 6 B Darshan Institute of Engineering & Technology

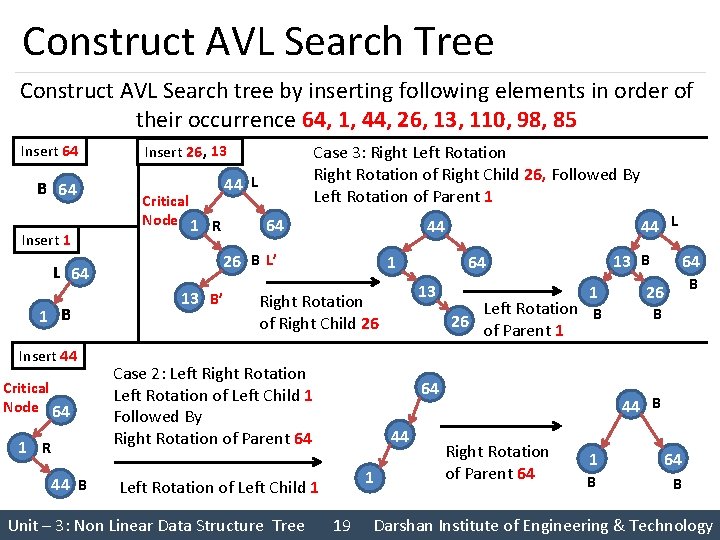
Construct AVL Search Tree Construct AVL Search tree by inserting following elements in order of their occurrence 64, 1, 44, 26, 13, 110, 98, 85 Insert 64 B 64 Insert 1 Insert 26 , 13 Critical Node 1 R Insert 44 Critical Node 64 1 R 44 B 44 L 64 13 B’ 1 Case 2: Left Right Rotation Left Rotation of Left Child 1 Followed By Right Rotation of Parent 64 13 B 64 13 Right Rotation of Right Child 26 1 26 Left Rotation B of Parent 1 64 44 1 Left Rotation of Left Child 1 Unit – 3: Non Linear Data Structure Tree 44 L 44 26 B L’ L 64 1 B Case 3: Right Left Rotation Right Rotation of Right Child 26, Followed By Left Rotation of Parent 1 19 64 B 26 B 44 B Right Rotation of Parent 64 1 64 B B Darshan Institute of Engineering & Technology

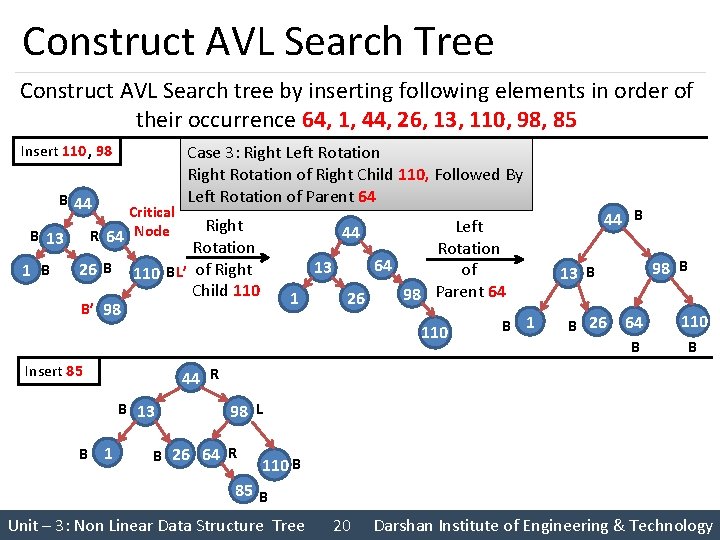
Construct AVL Search Tree Construct AVL Search tree by inserting following elements in order of their occurrence 64, 1, 44, 26, 13, 110, 98, 85 Insert 110 , 98 B 44 Critical R 64 Node B 13 1 B 26 B B’ 98 Case 3: Right Left Rotation Right Rotation of Right Child 110, Followed By Left Rotation of Parent 64 Right Rotation 110 B L’ of Right Child 110 Left 44 Rotation 64 13 of 98 Parent 64 26 1 110 Insert 85 98 B 13 B B 26 64 110 B B 44 R B 13 B 1 44 B 98 L B 26 64 R 110 B 85 B Unit – 3: Non Linear Data Structure Tree 20 Darshan Institute of Engineering & Technology

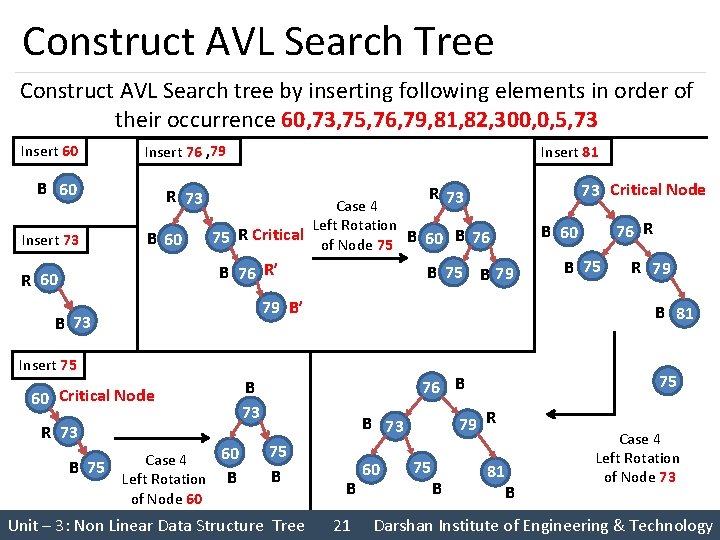
Construct AVL Search Tree Construct AVL Search tree by inserting following elements in order of their occurrence 60, 73, 75, 76, 79, 81, 82, 300, 0, 5, 73 Insert 60 Insert 76 , 79 B 60 Insert 73 R 73 B 60 Insert 81 Case 4 Left Rotation 75 R Critical of Node 75 B 60 B 76 R’ R 60 B 75 B 79 79 B’ B 73 60 Critical Node B 75 60 Case 4 Left Rotation B of Node 60 79 R B 73 Unit – 3: Non Linear Data Structure Tree B 75 R 79 75 76 B B 73 75 B 76 R B 60 B 81 Insert 75 R 73 73 Critical Node R 73 B 21 60 75 B 81 B Case 4 Left Rotation of Node 73 Darshan Institute of Engineering & Technology

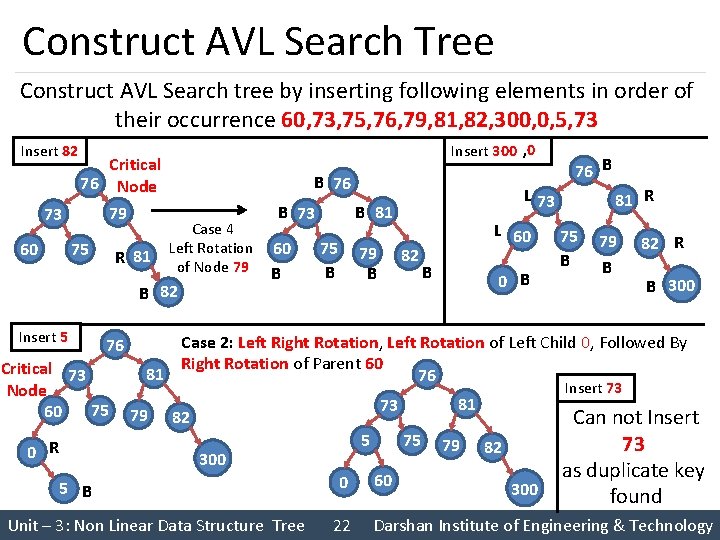
Construct AVL Search Tree Construct AVL Search tree by inserting following elements in order of their occurrence 60, 73, 75, 76, 79, 81, 82, 300, 0, 5, 73 Insert 82 73 60 Critical 76 Node 79 75 R 81 Insert 300 , 0 B 76 Case 4 Left Rotation of Node 79 B 82 Insert 5 76 Critical 73 Node 75 60 0 R 60 B L 73 B 81 B 73 75 B 79 B 76 B 82 L 60 B 81 R 75 B 79 B 82 R B 300 Case 2: Left Right Rotation, Left Rotation of Left Child 0, Followed By Right Rotation of Parent 60 81 76 79 81 73 82 5 300 5 B Unit – 3: Non Linear Data Structure Tree 0 22 75 60 Insert 73 79 82 300 Can not Insert 73 as duplicate key found Darshan Institute of Engineering & Technology

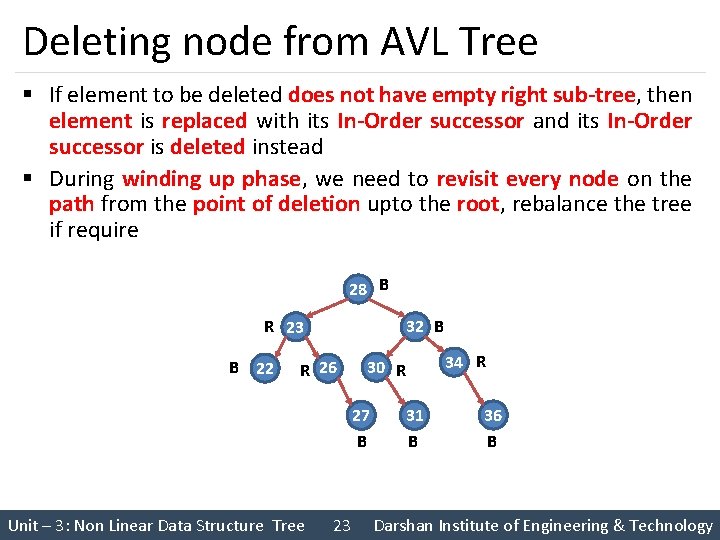
Deleting node from AVL Tree § If element to be deleted does not have empty right sub-tree, then element is replaced with its In-Order successor and its In-Order successor is deleted instead § During winding up phase, we need to revisit every node on the path from the point of deletion upto the root, rebalance the tree if require 28 B 32 B R 23 B 22 R 26 27 B Unit – 3: Non Linear Data Structure Tree 23 34 R 30 R 31 B 36 B Darshan Institute of Engineering & Technology

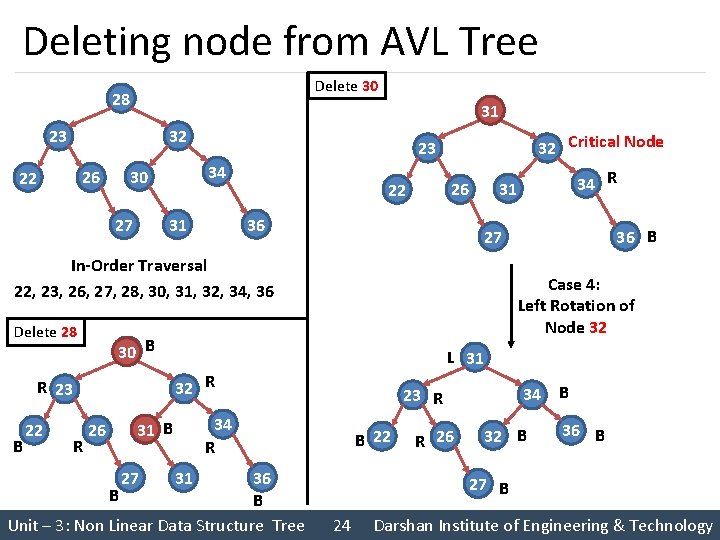
Deleting node from AVL Tree Delete 30 28 30 31 32 23 26 22 34 30 27 32 Critical Node 23 31 26 22 36 B 22 R Case 4: Left Rotation of Node 32 28 B 30 L 31 32 R R 23 26 36 B B Unit – 3: Non Linear Data Structure Tree 34 B 23 R 34 R 30 31 B 27 36 B 27 In-Order Traversal 22, 23, 26, 27, 28, 30, 31, 32, 34, 36 Delete 28 34 R 31 B 22 31 R 26 32 B 36 B 27 B 24 Darshan Institute of Engineering & Technology

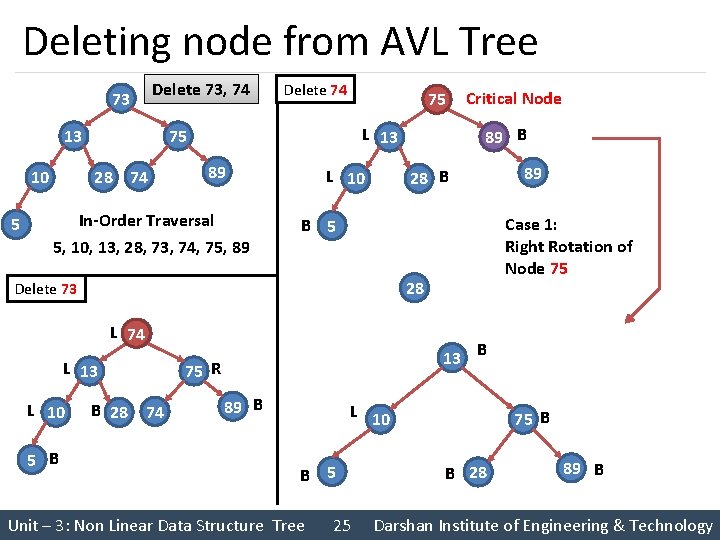
Deleting node from AVL Tree 73 Delete 73, 74 5 75 74 L 13 75 13 28 74 10 Delete 74 89 In-Order Traversal 5, 10, 13, 28, 73, 74, 75, 89 L 10 75 B 89 Case 1: Right Rotation of Node 75 B 5 28 L 74 73 L 13 5 B 89 28 B Delete 73 L 10 Critical Node B 28 74 13 75 R 89 B B L 10 B 5 Unit – 3: Non Linear Data Structure Tree 25 75 B B 28 89 B Darshan Institute of Engineering & Technology

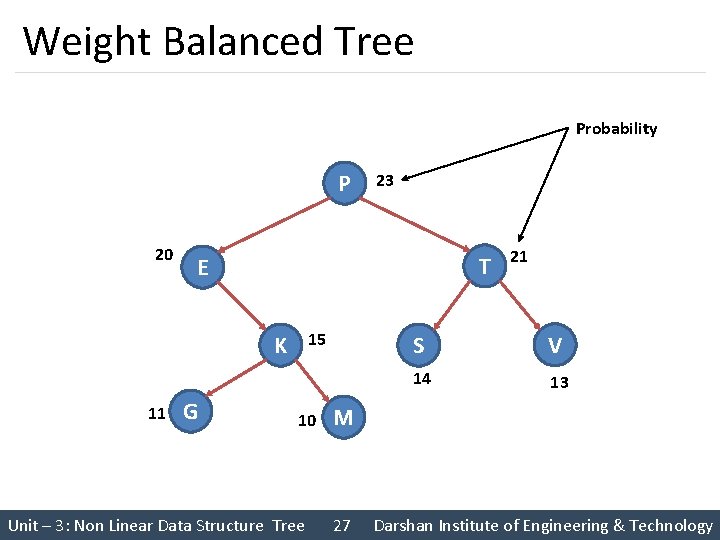
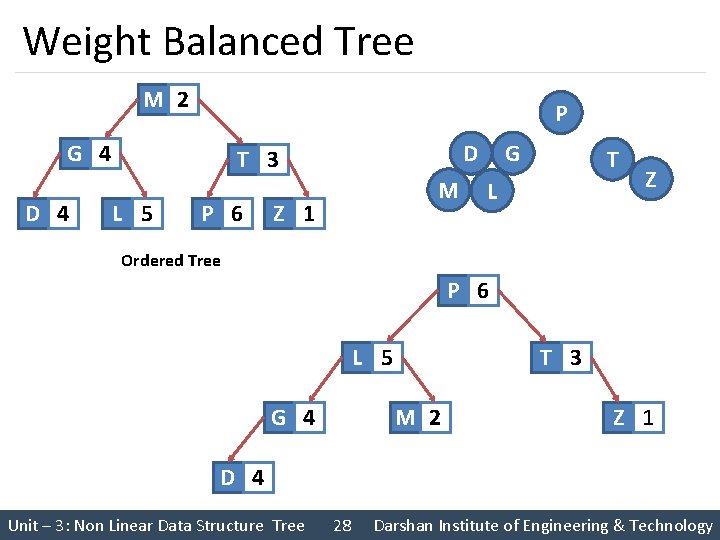
Weight Balanced Tree § In a weight balanced tree, the nodes are arranged on the basis of the knowledge available on the probability for searching each node § The node with highest probability is placed at the root of the tree § The nodes in the left sub-tree are less in ranking as well as less in probability then the root node § The nodes in the right sub-tree are higher in ranking but less in probability then the root node § Each node of such a Tree has an information field contains the value of the node and count number of times node has been visited Unit – 3: Non Linear Data Structure Tree 26 Darshan Institute of Engineering & Technology

Weight Balanced Tree Probability P 20 T E 15 K 11 23 G 10 Unit – 3: Non Linear Data Structure Tree 21 S V 14 13 M 27 Darshan Institute of Engineering & Technology

Weight Balanced Tree M 2 P G 4 D T 3 L 5 P 6 M Z 1 G T L Z Ordered Tree P 6 L 5 G 4 T 3 M 2 Z 1 D 4 Unit – 3: Non Linear Data Structure Tree 28 Darshan Institute of Engineering & Technology

Multiway Search Tree (B - Tree) § The nodes in a binary tree like AVL tree contains only one record § AVL tree is commonly stored in primary memory § In database applications where huge volume of data is handled, the search tree can not be accommodated in primary memory § B-Trees are primarily meant for secondary storage § B-Tree is a M-way tree which can have maximum of M Children 10, 15, 20 2, 3 11, 14 16 21 4 – way Tree Unit – 3: Non Linear Data Structure Tree 29 Darshan Institute of Engineering & Technology

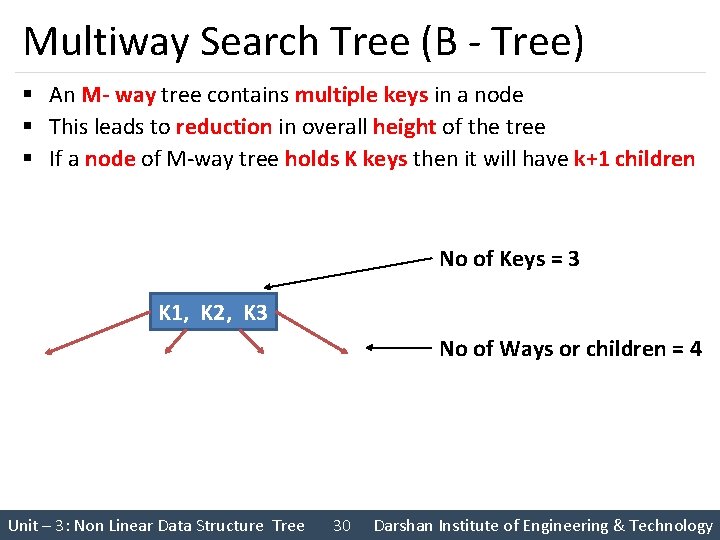
Multiway Search Tree (B - Tree) § An M- way tree contains multiple keys in a node § This leads to reduction in overall height of the tree § If a node of M-way tree holds K keys then it will have k+1 children No of Keys = 3 K 1, K 2, K 3 No of Ways or children = 4 Unit – 3: Non Linear Data Structure Tree 30 Darshan Institute of Engineering & Technology

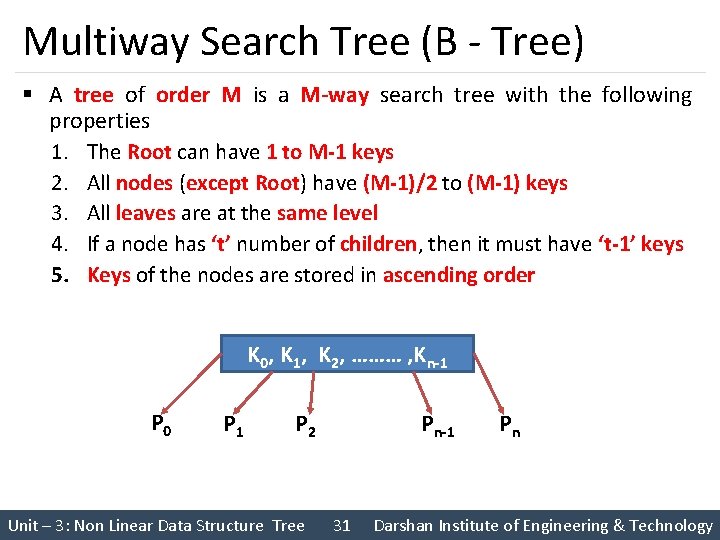
Multiway Search Tree (B - Tree) § A tree of order M is a M-way search tree with the following properties 1. The Root can have 1 to M-1 keys 2. All nodes (except Root) have (M-1)/2 to (M-1) keys 3. All leaves are at the same level 4. If a node has ‘t’ number of children, then it must have ‘t-1’ keys 5. Keys of the nodes are stored in ascending order K 0, K 1, K 2, ……… , Kn-1 P 0 P 1 P 2 Unit – 3: Non Linear Data Structure Tree Pn-1 31 Pn Darshan Institute of Engineering & Technology

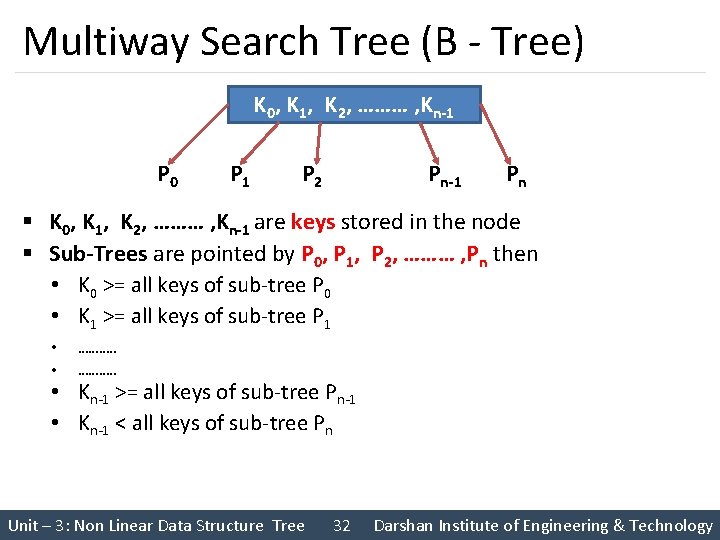
Multiway Search Tree (B - Tree) K 0, K 1, K 2, ……… , Kn-1 P 0 P 1 P 2 Pn-1 Pn § K 0, K 1, K 2, ……… , Kn-1 are keys stored in the node § Sub-Trees are pointed by P 0, P 1, P 2, ……… , Pn then • K 0 >= all keys of sub-tree P 0 • K 1 >= all keys of sub-tree P 1 • • ………. . • Kn-1 >= all keys of sub-tree Pn-1 • Kn-1 < all keys of sub-tree Pn Unit – 3: Non Linear Data Structure Tree 32 Darshan Institute of Engineering & Technology

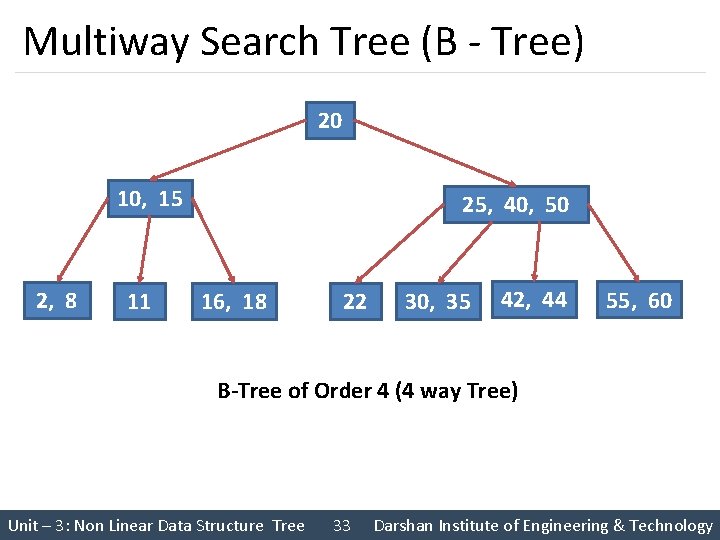
Multiway Search Tree (B - Tree) 20 10, 15 2, 8 11 25, 40, 50 16, 18 22 30, 35 42, 44 55, 60 B-Tree of Order 4 (4 way Tree) Unit – 3: Non Linear Data Structure Tree 33 Darshan Institute of Engineering & Technology

Insertion of Key in B-Tree 1. If Root is NULL, construct a node and insert key 2. If Root is NOT NULL I. Find the correct leaf node to which key should be added II. If leaf node has space to accommodate key, it is inserted and sorted III. If leaf node does not have space to accommodate key, we split node into two parts Unit – 3: Non Linear Data Structure Tree 34 Darshan Institute of Engineering & Technology

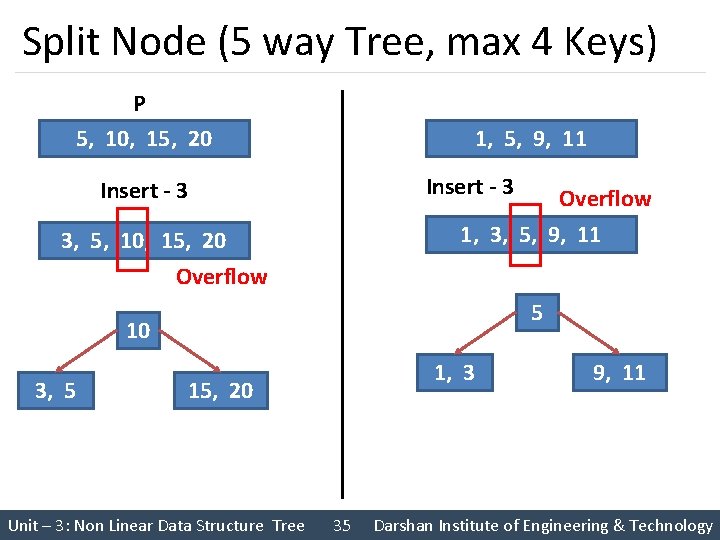
Split Node (5 way Tree, max 4 Keys) P 5, 10, 15, 20 1, 5, 9, 11 Insert - 3 Overflow 1, 3, 5, 9, 11 3, 5, 10, 15, 20 Overflow 5 10 3, 5 1, 3 15, 20 Unit – 3: Non Linear Data Structure Tree 35 9, 11 Darshan Institute of Engineering & Technology

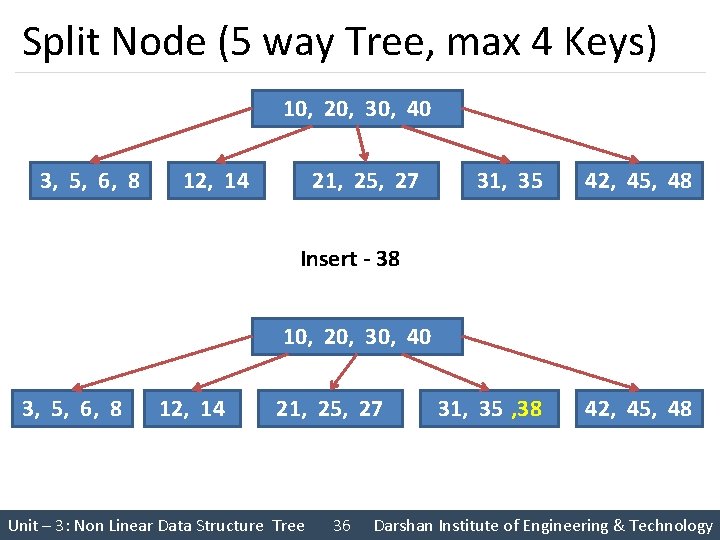
Split Node (5 way Tree, max 4 Keys) 10, 20, 30, 40 3, 5, 6, 8 12, 14 21, 25, 27 31, 35 42, 45, 48 31, 35 , 38 42, 45, 48 Insert - 38 10, 20, 30, 40 3, 5, 6, 8 12, 14 21, 25, 27 Unit – 3: Non Linear Data Structure Tree 36 Darshan Institute of Engineering & Technology

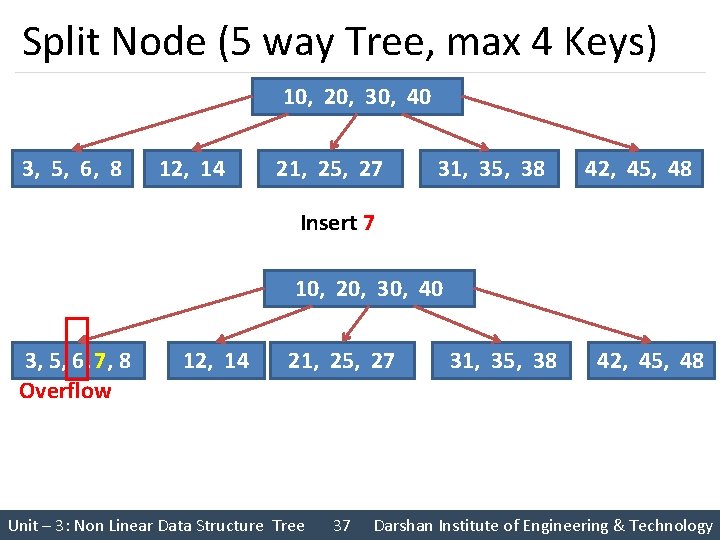
Split Node (5 way Tree, max 4 Keys) 10, 20, 30, 40 3, 5, 6, 8 12, 14 21, 25, 27 31, 35, 38 42, 45, 48 Insert 7 10, 20, 30, 40 3, 5, 6, 7, 8 Overflow 12, 14 21, 25, 27 Unit – 3: Non Linear Data Structure Tree 37 31, 35, 38 42, 45, 48 Darshan Institute of Engineering & Technology

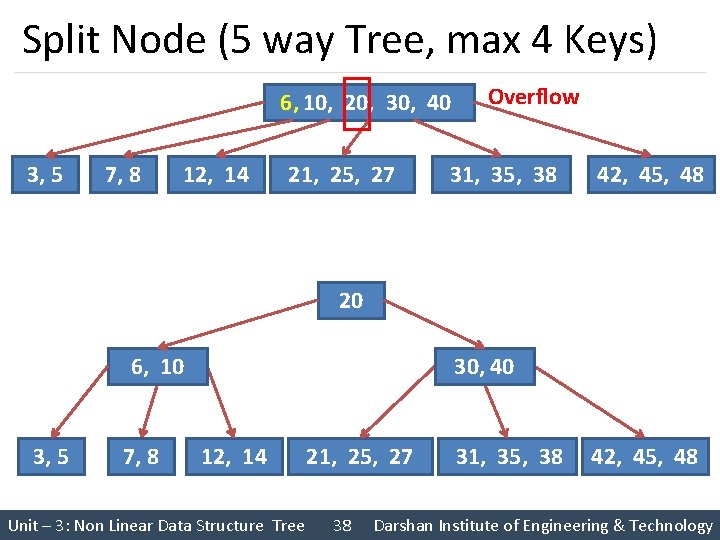
Split Node (5 way Tree, max 4 Keys) 6, 10, 20, 30, 40 3, 5 7, 8 12, 14 21, 25, 27 Overflow 31, 35, 38 42, 45, 48 20 6, 10 3, 5 7, 8 30, 40 12, 14 Unit – 3: Non Linear Data Structure Tree 21, 25, 27 38 31, 35, 38 42, 45, 48 Darshan Institute of Engineering & Technology

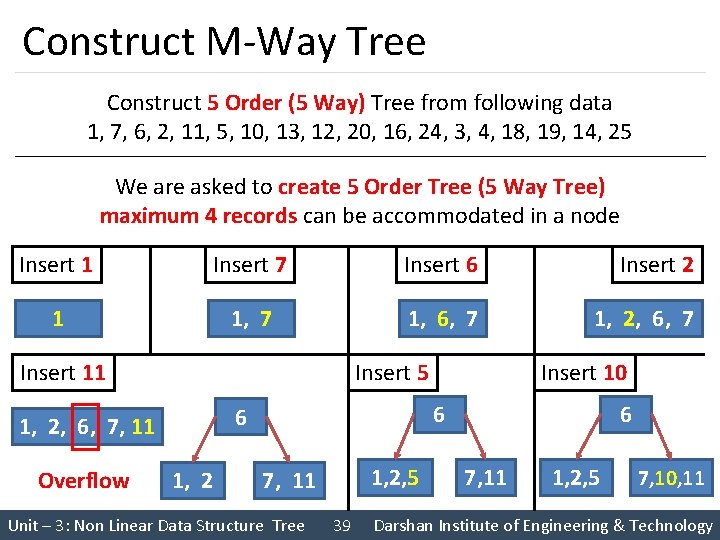
Construct M-Way Tree Construct 5 Order (5 Way) Tree from following data 1, 7, 6, 2, 11, 5, 10, 13, 12, 20, 16, 24, 3, 4, 18, 19, 14, 25 We are asked to create 5 Order Tree (5 Way Tree) maximum 4 records can be accommodated in a node Insert 1 Insert 7 Insert 6 Insert 2 1 1, 7 1, 6, 7 1, 2, 6, 7 Insert 11 Insert 5 Overflow 6 6 1, 2, 6, 7, 11 1, 2 Insert 10 1, 2, 5 7, 11 Unit – 3: Non Linear Data Structure Tree 39 6 7, 11 1, 2, 5 7, 10, 11 Darshan Institute of Engineering & Technology

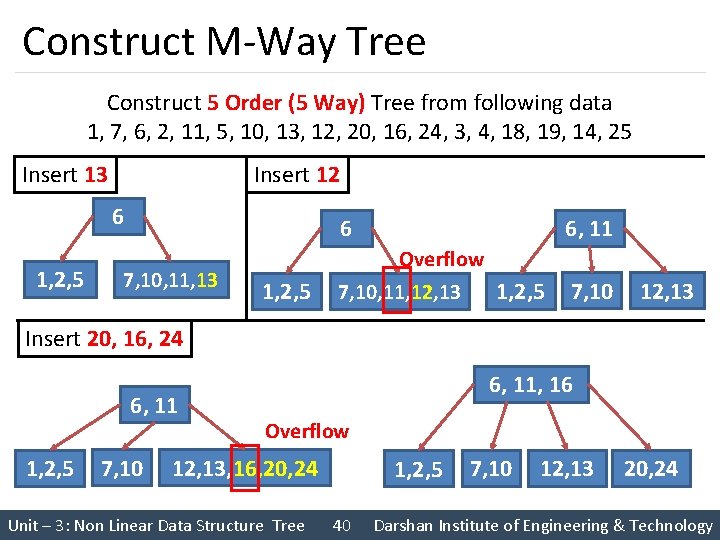
Construct M-Way Tree Construct 5 Order (5 Way) Tree from following data 1, 7, 6, 2, 11, 5, 10, 13, 12, 20, 16, 24, 3, 4, 18, 19, 14, 25 Insert 13 Insert 12 6 1, 2, 5 7, 10, 11, 13 1, 2, 5 6 6, 11 Overflow 7, 10, 11, 12, 13 1, 2, 5 7, 10 12, 13 Insert 20, 16, 24 6, 11 1, 2, 5 7, 10 6, 11, 16 Overflow 12, 13, 16, 20, 24 Unit – 3: Non Linear Data Structure Tree 1, 2, 5 40 7, 10 12, 13 20, 24 Darshan Institute of Engineering & Technology

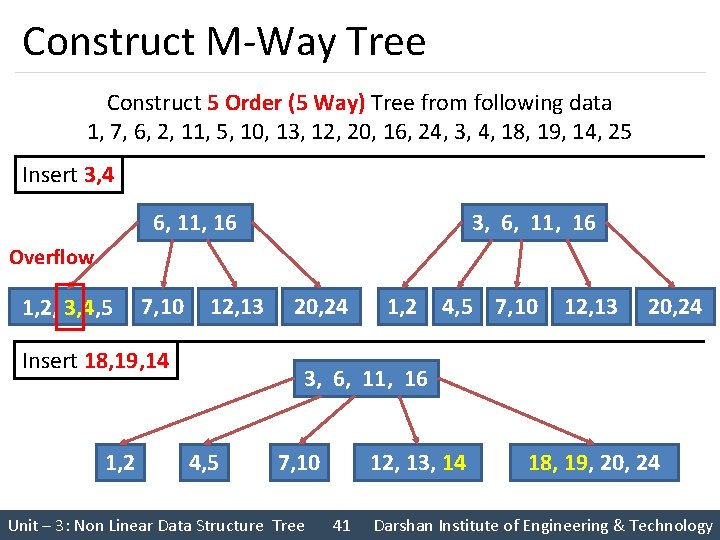
Construct M-Way Tree Construct 5 Order (5 Way) Tree from following data 1, 7, 6, 2, 11, 5, 10, 13, 12, 20, 16, 24, 3, 4, 18, 19, 14, 25 Insert 3, 4 3, 6, 11, 16 Overflow 1, 2, 3, 4, 5 7, 10 12, 13 Insert 18, 19, 14 1, 2 20, 24 1, 2 4, 5 7, 10 12, 13 20, 24 3, 6, 11, 16 4, 5 7, 10 Unit – 3: Non Linear Data Structure Tree 12, 13, 14 41 18, 19, 20, 24 Darshan Institute of Engineering & Technology

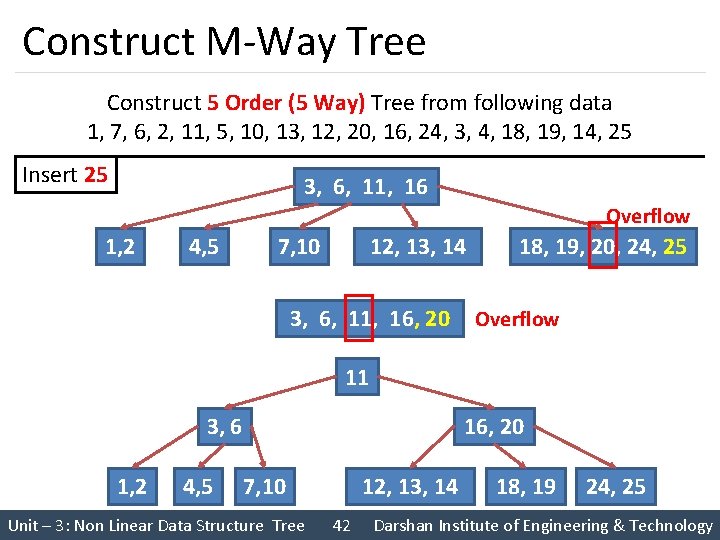
Construct M-Way Tree Construct 5 Order (5 Way) Tree from following data 1, 7, 6, 2, 11, 5, 10, 13, 12, 20, 16, 24, 3, 4, 18, 19, 14, 25 Insert 25 3, 6, 11, 16 Overflow 1, 2 4, 5 7, 10 12, 13, 14 3, 6, 11, 16, 20 18, 19, 20, 24, 25 Overflow 11 3, 6 1, 2 4, 5 16, 20 7, 10 Unit – 3: Non Linear Data Structure Tree 12, 13, 14 42 18, 19 24, 25 Darshan Institute of Engineering & Technology