Unit 3 Linear Relationships Lesson 4 Proportional Relationships

Unit 3 Linear Relationships Lesson 4 Proportional Relationships

Lesson 4: Proportional Relationships Objective: SWBAT find the rate of change, unit rate or slope and determine if it is a proportional relationship. Do Now:

Lesson 4: Proportional Relationships A relationship between two quantities is proportional if: –it has a constant ratio (y/x) –it is a straight line –the line passes through the origin Proportional Relationships are written in the form y = mx. “m” is the slope, rate of change or unit rate

Lesson 4: Proportional Relationships When the ratio of y to x is a constant, we say y varies directly with x. “m” will represent the constant of variation or proportionality m=y x Equation: y = mx is a direct variation

Lesson 4: Proportional Relationships Example #1: Given the constant of variation (constant ratio) m=3 constant of variation y =mx Direct variation equation y = 3 x Is it a Proportional Relationship?

Lesson 4: Proportional Relationships Example #2: Y varies directly with x, if y=12 and x=3, find the constant of variation and write the direct variation equation. m=y m = 12 = 4 x 3 y =mx Direct variation equation y = 4 x Is this a Proportional Relationship?

Lesson 4: Proportional Relationships Example #3: Given a table of x, y values Time Amount 1 12 2 24 3 36 Slope (rate of change): 24 – 12 = 12 2– 1 Constant Ratio m=y x (unit price): 12 24 1 2 Direct Variation Equation: y = 12 x 36 – 24 = 12 2 -1 36 = 12 3

Lesson 4: Proportional Relationships Example #4: Given a table of x, y values Time Amount 1 10. 2 2 10. 4 3 10. 6 Slope (rate of change): 10. 4 – 10. 2 =. 2 2– 1 Constant Ratio (unit price): m=y 10. 2 ≠ 10. 4 ≠ x 1 2 Is this a Proportional Relationship? 10. 6 3 10. 6 – 10. 4 =. 2 2 -1

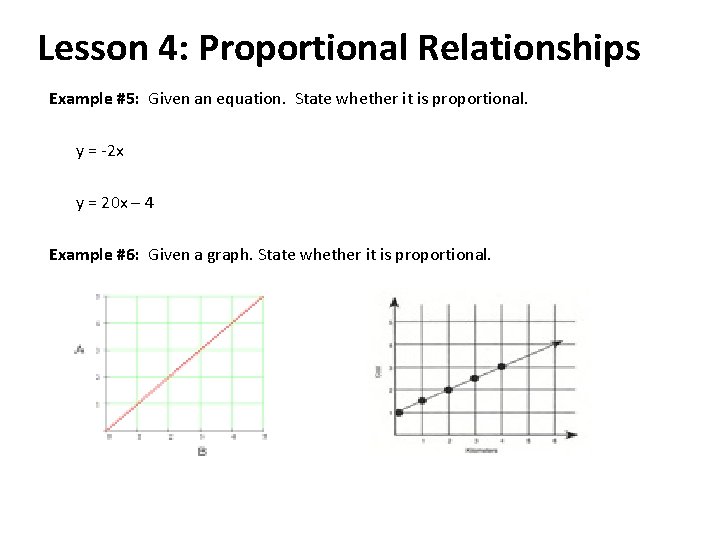
Lesson 4: Proportional Relationships Example #5: Given an equation. State whether it is proportional. y = -2 x y = 20 x – 4 Example #6: Given a graph. State whether it is proportional.

Practice • • Guided Practice Independent Practice Extra Practice Handout 4

Closure Question: What is the constant of variation in a direct variation? Exit Ticket Homework: Homework 4

Exit Ticket Y varies directly with X. If y = 16 and x=2, find the constant of variation and write the direct variation equation.