Unit 3 Lesson 6 Constant of Proportionality and

Proportional relationships vary directly and we say that they are direct variations. These are

We can find the constant of proportionality from a table of values, equation and

Example: Find the constant of proportionality: Apples (lbs) 2 2. 5 3 3. 5

Find the constant of proportionality. X Y 2 1. 5 5 3. 75 10

In an equation, write the equation in the form y = kx to find

Find the constant of proportionality: (click to reveal)

In a graph, choose a point (x, y) to find and simplify the ratio

Example: Find the constant of proportionality. 20 18 16 14 12 10 8 6

Find the constant of proportionality. 40 36 32 28 24 20 16 12 8

Constant of proportionality & unit rate are equivalent. We can use the constant of

Example: You are buying Jersey Tomatoes for a cost of 2 pounds for $3.

Example: At the candy store, you purchase 5 lbs for $22. 45. Write an

Write an equation that represents the proportional relationship. The total cost (c) of grapes

Write an equation that represents the proportional relationship. 5 A B 4. 5 4

Write an equation that represents the proportional relationship. Days, d 2 3 4 5

Slides: 16

Download presentation

Unit 3, Lesson 6 Constant of Proportionality and Writing Direct Variation Equations

Proportional relationships vary directly and we say that they are direct variations. These are linear (line) relationships and have an equation that describes the relationship. The constant of proportionality in a direct variation is a constant ratio (unit rate) in any proportional relationship. We use the letter k to represent the constant of proportionality. Equations: y = kx or k= y x

We can find the constant of proportionality from a table of values, equation and a graph. In a table, simplify any one of the ratios. Chaperones 1 2 3 4 5 Students 12 24 36 48 60

Example: Find the constant of proportionality: Apples (lbs) 2 2. 5 3 3. 5 4 Cost ($) 3. 96 4. 95 5. 94 6. 93 7. 92

Find the constant of proportionality. X Y 2 1. 5 5 3. 75 10 7. 5 12 9

In an equation, write the equation in the form y = kx to find k. Examples: Y=5 x Y=¼x Y=3. 5 x

Find the constant of proportionality: (click to reveal)

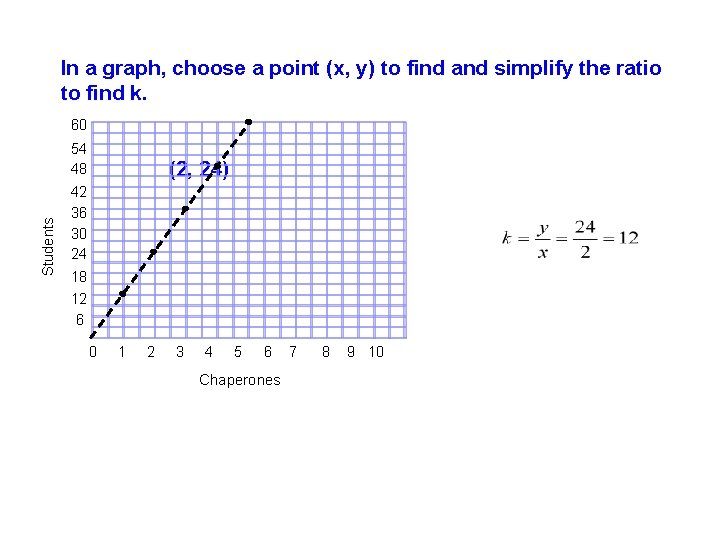
In a graph, choose a point (x, y) to find and simplify the ratio to find k. Students 60 54 48 42 36 30 24 18 12 6 (2, 24) 0 1 2 3 4 5 6 Chaperones 7 8 9 10

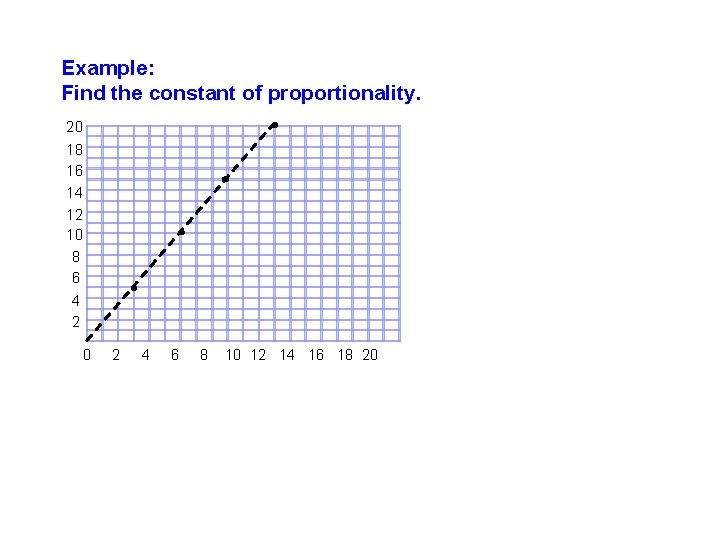
Example: Find the constant of proportionality. 20 18 16 14 12 10 8 6 4 2 0 2 4 6 8 10 12 14 16 18 20

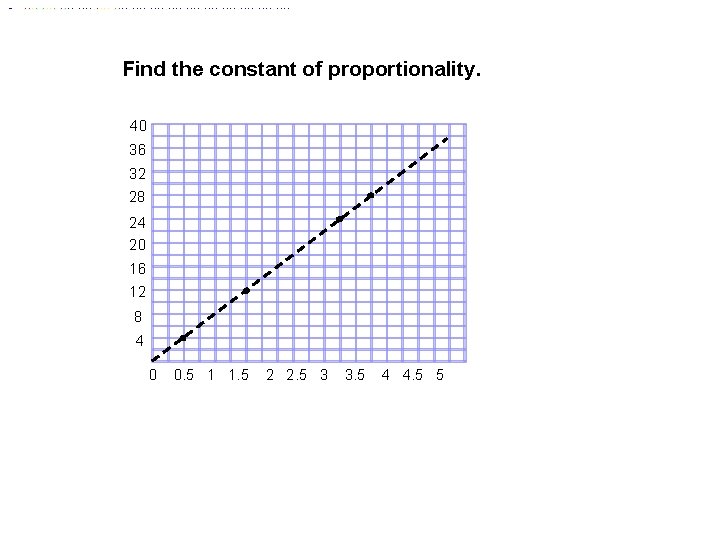
Find the constant of proportionality. 40 36 32 28 24 20 16 12 8 4 0 0. 5 1 1. 5 2 2. 5 3 3. 5 4 4. 5 5

Constant of proportionality & unit rate are equivalent. We can use the constant of proportionality to help write equations using proportional relationships. By transforming the equation from: to y = kx, we can write an equation that can be applied to various situations. X is the independent (input) variable and y is the dependent (output) variable. This means that a change in x will effect y.

Example: You are buying Jersey Tomatoes for a cost of 2 pounds for $3. 98. Write an equation to represent the proportional relationship. • Let c = cost p = pounds • Determine the unit rate: • Write an equation to relate the two quantities:

Example: At the candy store, you purchase 5 lbs for $22. 45. Write an equation to represent the proportional relationship. • Let c = cost p = pounds • Determine the unit rate: • Write an equation to relate the two quantities:

Write an equation that represents the proportional relationship. The total cost (c) of grapes for $1. 40 per pound(p) A c = 1. 4 p B p = 1. 4 c

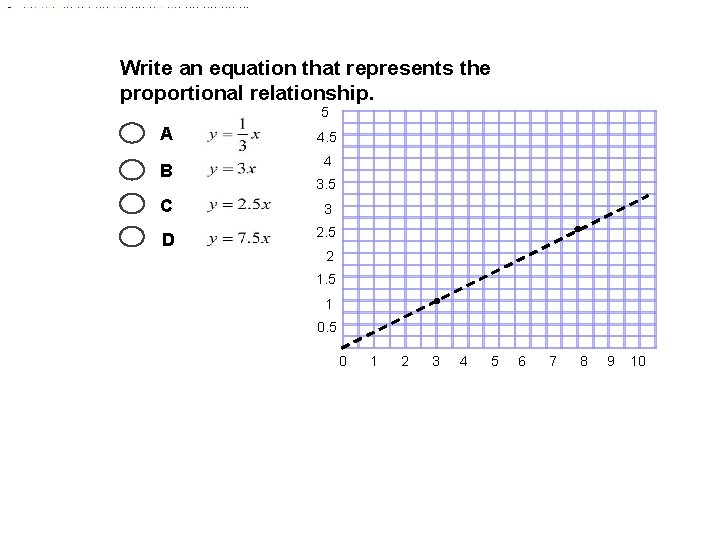
Write an equation that represents the proportional relationship. 5 A B 4. 5 4 3. 5 C 3 D 2. 5 2 1. 5 1 0. 5 0 1 2 3 4 5 6 7 8 9 10

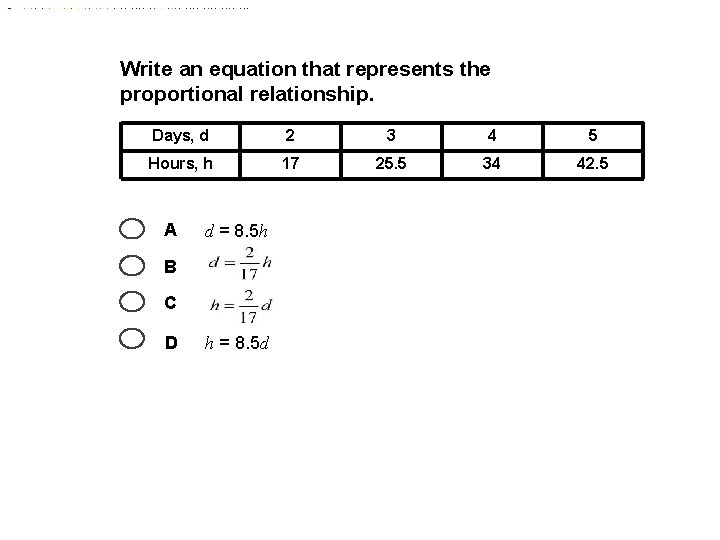
Write an equation that represents the proportional relationship. Days, d 2 3 4 5 Hours, h 17 25. 5 34 42. 5 A d = 8. 5 h B C D h = 8. 5 d