Unit 3 Intermediate code Generation Intermediate code Generation

Unit 3 Intermediate code Generation

Intermediate code Generation

Intermediate code Generation If the source language is translated to the target machine language by the compiler without the option of generating intermediate code, a native compiler is required for each of the new machine. The necessity of a new full compiler for each of the unique machine is eliminated by the Intermediate code, the analysis portion remaining the same for the compilers.

Intermediate code Generation In accordance with the target machine, the second part of the compiler, synthesis is changed. The source code modifications are easily applied for improving the performance of the code applying the code optimization techniques on intermediate code.

How the Intermediate Code is represented in Compiler Design There are many ways of representing Intermediate codes and each of the way has its own benefits. High Level The code that is close to the source language is High-Level intermediate code. They are easily generated from the source code and the code modifications can be easily applied for enhancing the performance of the source code. But it is not preferred for the target machine optimization. Low Level The code that is close to the target machine and which is made suitable for memory allocation, instruction set selection etc is known as Low Level Intermediate code. Machine-dependent optimizations benefits best from this code.

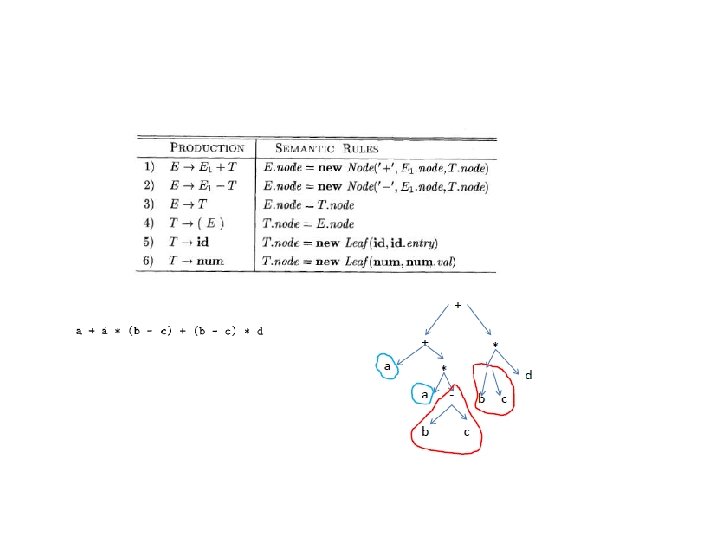
Three-Address Code in Compiler Design The input is received by the predecessor phase, semantic analyzer, in the form of annotated syntax tree by the Intermediate code generator. The syntax tree is then converted into a linear representation. The intermediate code is machine independent code and hence it is assumed by the code generator for having unlimited number of memory storage for generating the code.

Three-Address Code in Compiler Design a = b + c * d; This expression is divided into sub-expressions by the intermediate code generator and the corresponding code is generated. r 1 = c * d; r 2 = b + r 1; a = r 2 r being used as registers in the target program. A three-address code has three address locations used for calculating the expression and is represented in two forms - quadruples and triples.

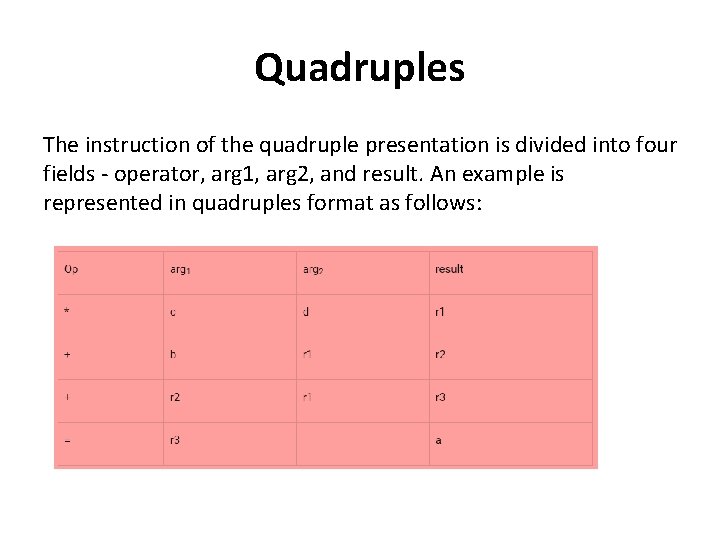
Quadruples The instruction of the quadruple presentation is divided into four fields - operator, arg 1, arg 2, and result. An example is represented in quadruples format as follows:

Triples The instruction of the Triples presentation is divided into three fields - op, arg 1, and arg 2. The position of the expression denotes the results of the respective subexpressions. The similarity with DAG and syntax tree is represented by triples. When expressions are represented, they are equivalent to DAG.

Indirect Triples The enhancement in the representation of triples is known as Indirect triples. The results are stored in pointers instead of position facilitating the optimizers to re-position the subexpression and produce the optimized code.

Synthesized attributes A Synthesized attribute is an attribute of the nonterminal on the left-hand side of a production. All of the attributes that we have used so far have been synthesized. Synthesized attributes represent information that is being passed up the parse tree.

Inherited attributes In general, attribute equations are allowed to define attributes of any of the nonterminals in a production, even those on the right-hand side. An attribute of a nonterminal on the right-hand side of a production is called an inherited attribute. Recall that a top-down parser needs a left-factored grammar. Let's look at such a grammar and derive attribute equations for it.

Inherited attributes Example The grammar is as follows. :

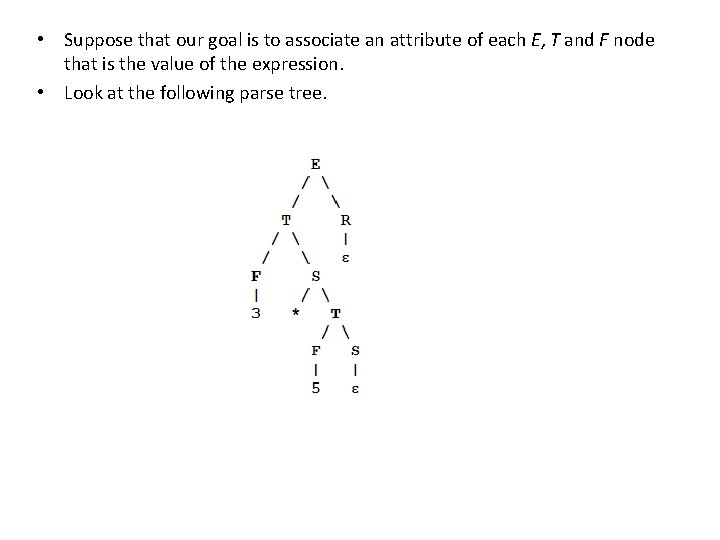
• Suppose that our goal is to associate an attribute of each E, T and F node that is the value of the expression. • Look at the following parse tree.

Each F node gets its value from the n token. But an S node that uses production S → * T needs to get the left-hand operand of * from its left sibling. The information needs to go across the tree. Here is the tree with attributes shown

L-attributed equations • Attribute equations only have one restriction: They must not be cyclic. You cannot • define attribute a in terms of attribute b, • define b in terms of c and • define c in terms of a. • But that does not prevent an attribute of one node in a parse tree from depending on an attribute of a node that will not be created until later. • (To handle that, the attribute equation solver would need to defer an equation until it could be used. ) • Normally, compiler designers avoid really strange attribute equations.

L-attributed equations • A set of attribute equations is L-attributed if each equation can be processed at the point where it is written. Specifically, • Synthesized attributes are allowed in L-attributed definitions. • Suppose that an attribute equation associated with production A → X 1 X 2 … Xn defines an attribute of Xi. • The right-hand side of that equation can use: – inherited attributes of A, and – inherited or synthesized attributes of X 1, X 2, …, Xi− 1

Inherited attributes with recursive descent • Inherited attributes in an L-attributed set of equations are easy to handle by recursive descent. • A synthesized attribute is a value returned by a syntactic function. • An inherited attribute is a parameter that is passed to a syntactic function. • That explains why the functions in the recursivedescent example are written the way they are.

Intermediate Languages AN INTERMEDIATE REPRESENTATION (IR) is a language for an abstract machine (or a language that can be easily evaluated by an abstract machine) It should not include too much machine specific detail. It provides a separation between front and back ends which helps compiler portability. Code generation and assignment of temporaries to registers are clearly separated from semantic analysis. It allows optimization independent of the target machine. Intermediate representations are by design more abstract and uniform, so optimization routines are simpler.

Properties of good intermediate representations. Convenient to produce in the semantic analysis phase. Convenient to translate into code for the desired target architecture. Each construct must have a clear and simple meaning such that optimizing transformations that rewrite the IR can be easily specified and implemented.

TREE-BASED INTERMEDIATE REPRESENTATIONS. The most obvious way to present the information gained from lexical and syntax analysis is a syntax tree. In C, the representation can be handled using a struct for each node:

� Assignment statements assign a value to a variable. This means that a variable can represent different values at different times.

� Assignment means to set a variable to a value. � When a variable has a value, it keeps that value until another value is assigned to it, or until the current set of code ends and the system no longer keeps track of the variable

� A statement in programming context is a single complete programming instruction that is written as code

� Certain function calls, such as the MESSAGE function, can be a statement on their own. They are known as function call statements � [return value : =] <Function Call> � Example: : MESSAGE function

� The syntax of an assignment statement is almost as easy as the syntax of the function call statement. The syntax is as follows � <variable> � Example : = <expression> : : Integer Number: =10;

The “colon equals” (: =) is known as the assignment operator. You use it to assign a value or an expression that evaluates to a value to a variable. : =

�A single programming statement may span several code lines; one code line may consist of multiple statements. � Therefore, the C/AL compiler must be able to detect when one statement ends and another statement begins. � [ <statement> { ; <statement> } ] � Example Integer Num: =10;

� Before you can assign a variable to a value, the type of the value must match the type of the variable. However, within limits, you can automatically convert certain types in an assignment operation.

You can convert variables of string data types (code and text) automatically from one to the other. For example, if Description is a variable of type Text, and Code. Number is a variable of type Code, the following statement is valid: � Code. Number : = Description � Automatic conversion does have limitations. For example, if the value of the Description text variable has more characters than the length of the Code. Number variable, an error occurs when the program runs and executes this statement. This type of error is known as a run-time error.

� Variables of the numeric data types (integer, decimal, option, and char) can convert automatically from one to another

Expression An expression specifies the information to generate a desired value. Similar to a variable and a constant, an expression has a type and a value. expression is evaluated at run time to determine its value. Quantity * Unit. Cost

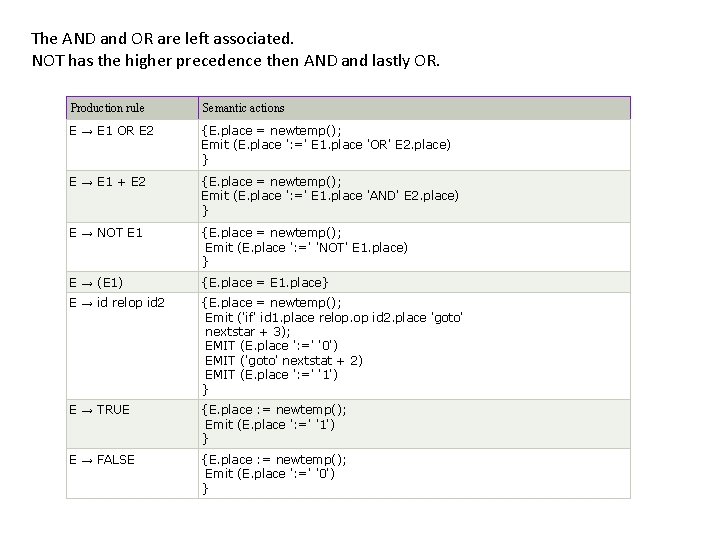
Boolean expressions have two primary purposes. They are used for computing the logical values. They are also used as conditional expression using if-then-else or while-do. Consider the grammar E → E OR E E → E AND E E → NOT E E → (E) E → id relop id E → TRUE E → FALSE

The AND and OR are left associated. NOT has the higher precedence then AND and lastly OR. Production rule Semantic actions E → E 1 OR E 2 {E. place = newtemp(); Emit (E. place ': =' E 1. place 'OR' E 2. place) } E → E 1 + E 2 {E. place = newtemp(); Emit (E. place ': =' E 1. place 'AND' E 2. place) } E → NOT E 1 {E. place = newtemp(); Emit (E. place ': =' 'NOT' E 1. place) } E → (E 1) {E. place = E 1. place} E → id relop id 2 {E. place = newtemp(); Emit ('if' id 1. place relop. op id 2. place 'goto' nextstar + 3); EMIT (E. place ': =' '0') EMIT ('goto' nextstat + 2) EMIT (E. place ': =' '1') } E → TRUE {E. place : = newtemp(); Emit (E. place ': =' '1') } E → FALSE {E. place : = newtemp(); Emit (E. place ': =' '0') }

The EMIT function is used to generate three address code and the newtemp( ) function is used to generate the temporary variables. The E → id relop id 2 contains the next_state and it gives the index of next three address statements in the output sequence. Here is the example which generates the three address code using the above translation scheme: p>q AND r<s OR u>r 100: if p>q goto 103 101: t 1: =0 102: goto 104 103: t 1: =1 104: if r>s goto 107 105: t 2: =0 106: goto 108 107: t 2: =1 108: if u>v goto 111 109: t 3: =0 110: goto 112 111: t 3: = 1 112: t 4: = t 1 AND t 2 113: t 5: = t 4 OR t 3

Statements that alter the flow of control The goto statement alters the flow of control. If we implement goto statements then we need to define a LABEL for a statement. A production can be added for this purpose: S → LABEL : S LABEL → id In this production system, semantic action is attached to record the LABEL and its value in the symbol table.

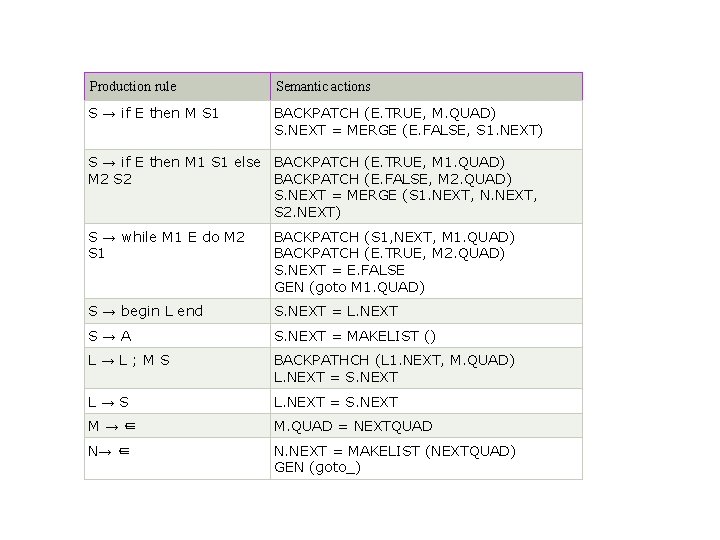
Following grammar used to incorporate structure flow-of-control constructs: S → if E then S else S S → while E do S S → begin L end S→ A L→ L ; S L→ S Here, S is a statement, L is a statement-list, A is an assignment statement. E is a Boolean-valued expression.

Translation scheme for statement that alters flow of control We introduce the marker non-terminal M as in case of grammar for Boolean expression. This M is put before statement in both if then else. In case of while-do, we need to put M before E as we need to come back to it after executing S. In case of if-then-else, if we evaluate E to be true, first S will be executed. After this we should ensure that instead of second S, the code after the if-then else will be executed. Then we place another non-terminal marker N after first S. The grammar is as follows: S → if E then M S else M S S → while M E do M S S → begin L end S→ A L→ L ; M S L→ S M→ ∈ N→ ∈

Production rule Semantic actions S → if E then M S 1 BACKPATCH (E. TRUE, M. QUAD) S. NEXT = MERGE (E. FALSE, S 1. NEXT) S → if E then M 1 S 1 else BACKPATCH (E. TRUE, M 1. QUAD) M 2 S 2 BACKPATCH (E. FALSE, M 2. QUAD) S. NEXT = MERGE (S 1. NEXT, N. NEXT, S 2. NEXT) S → while M 1 E do M 2 S 1 BACKPATCH (S 1, NEXT, M 1. QUAD) BACKPATCH (E. TRUE, M 2. QUAD) S. NEXT = E. FALSE GEN (goto M 1. QUAD) S → begin L end S. NEXT = L. NEXT S→A S. NEXT = MAKELIST () L→L; MS BACKPATHCH (L 1. NEXT, M. QUAD) L. NEXT = S. NEXT L→S L. NEXT = S. NEXT M→∈ M. QUAD = NEXTQUAD N→ ∈ N. NEXT = MAKELIST (NEXTQUAD) GEN (goto_)

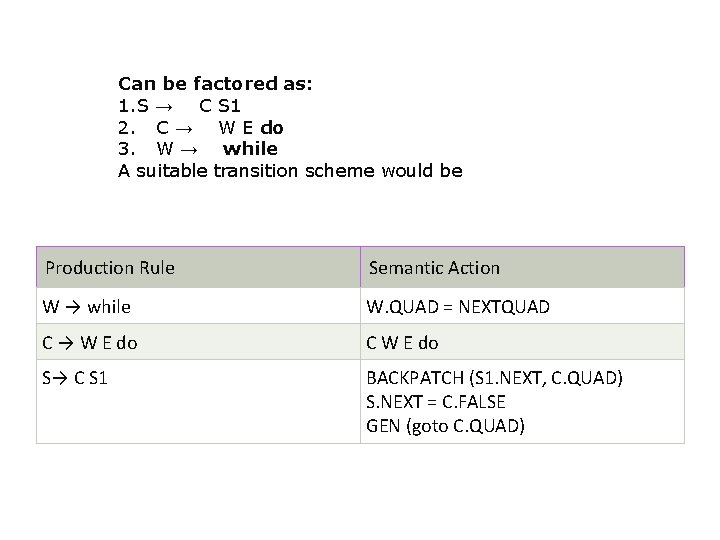
Postfix Translation In a production A → α, the translation rule of A. CODE consists of the concatenation of the CODE translations of the non-terminals in α in the same order as the non-terminals appear in α. Production can be factored to achieve postfix form. Postfix translation of while statement The production 1. S → while M 1 E do M 2 S 1

Can be factored as: 1. S → C S 1 2. C → W E do 3. W → while A suitable transition scheme would be Production Rule Semantic Action W → while W. QUAD = NEXTQUAD C → W E do C W E do S→ C S 1 BACKPATCH (S 1. NEXT, C. QUAD) S. NEXT = C. FALSE GEN (goto C. QUAD)

Postfix translation of for statement The production S for L = E 1 step E 2 to E 3 do S 1 Can be factored as F → for L T → F = E 1 by E 2 to E 3 do S → T S 1