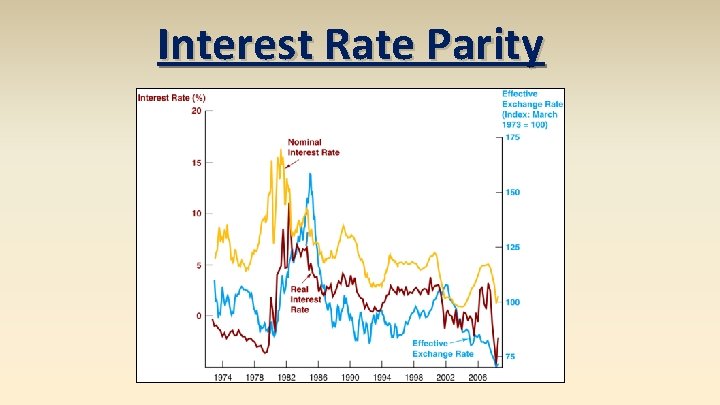
Unit 3 Exchange Rates Foreign Exchange 3212012 Exchange






















 Ro. R* = [E(et+1)/et](1 +](https://slidetodoc.com/presentation_image_h/325ed04924a6e58f922f05eaed9d2382/image-26.jpg)
 Ro. R* = [E(et+1)/et](1](https://slidetodoc.com/presentation_image_h/325ed04924a6e58f922f05eaed9d2382/image-27.jpg)




- Slides: 46

Unit 3: Exchange Rates Foreign Exchange 3/21/2012

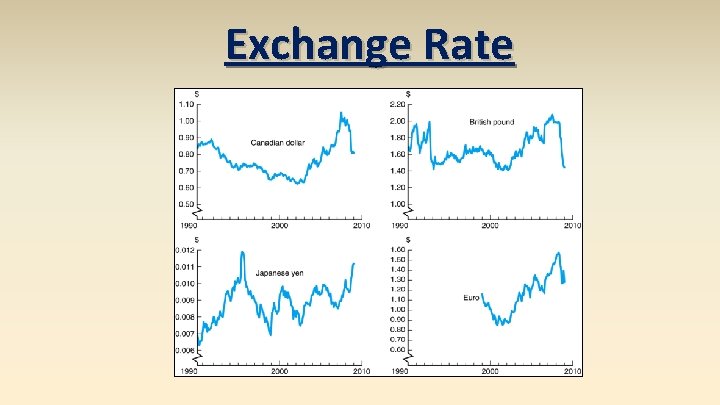
Exchange Rate exchange rate – price of one currency in terms of another For example: dollars/euro ($/€) or euros/dollar €/$) It is important to specify which is the denominator!

Exchange Rate Unless otherwise specified, our convention will be: e ≡ exchange rate (in $/€)

Exchange Rate spot transaction – immediate (2 day) exchange of bank deposits spot exchange rate – exchange rate for spot transactions; exchange rate for immediate (2 day) exchange of bank deposits

Exchange Rate forward transaction – exchange of bank deposits at some future date forward exchange rate – exchange rate forward transactions; exchange rate for exchange of bank deposits at some future date

Exchange Rate foreign exchange market – the financial market where exchange rates are determined

Exchange Rate appreciation – when a currency increases in value relative to another currency depreciation – when a currency decreases in value relative to another currency

Exchange Rate • appreciation o country’s goods abroad become more expensive o foreign goods in the country become cheaper o (€/$)↑ means dollar appreciates o ($/€)↓ means dollar appreciates o e↓ means dollar appreciates (e ≡ $/€)

Exchange Rate • depreciation o country’s goods abroad become cheaper o foreign goods in the country become more expensive o (€/$)↓ means dollar depreciates o ($/€)↑ means dollar depreciates o e↑ means dollar depreciates (e ≡ $/€)

Exchange Rate

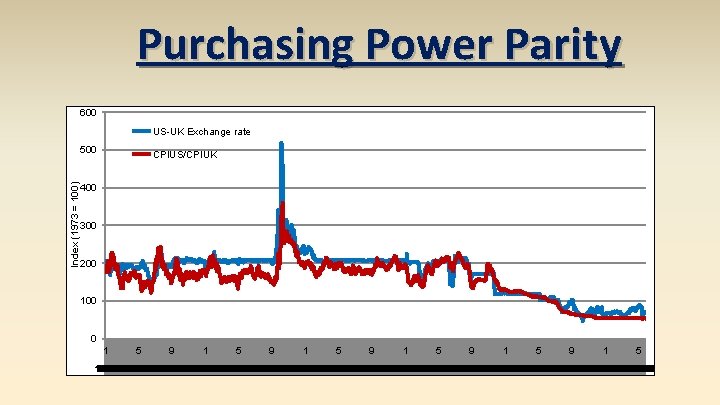
Purchasing Power Parity There can be only one! law of one price (LOOP) – the price of a good should be the same throughout the world (assuming transportation costs and trade barriers are low) e. g. , if steel costs $100/ton in America and € 50/ton in Europe, then the exchange rate should be e = 2 $/€

Purchasing Power Parity arbitrage – taking advantage of a price difference between two markets Arbitrage causes the law of one price (LOOP). If prices are different, an entrepreneur can buy steel in the cheaper country and sell it in the more expensive country for a profit.

Purchasing Power Parity $ € theory of purchasing power parity (PPP) – exchange rates between any two currencies will adjust to reflect changes in the price levels of the two countries e. g. , if the euro price level rises 10%, the dollar will appreciate 10%.

Purchasing Power Parity $ PPP in math form e. P*/P = 1 e = P/P* € • e ≡ exchange rate (in $/€) • P ≡ domestic price level (in $) • P* ≡ foreign price level (in €)

Purchasing Power Parity $ € PPP assumptions • all goods are identical • trade barriers are low • transportation costs are low • all goods traded across borders • all services traded across borders These assumptions do not hold in the real world. PPP works in the long run, but not the short run.

Purchasing Power Parity 600 US-UK Exchange rate Index (1973 = 100) 500 CPIUS/CPIUK 400 300 200 100 0 1 5 9 1 5 9 1 5 1794 1795 1796 1797 1798 1799 1800 1801 1802 1803 1804 1805 1806 1807 1808 1809 1810 1811 1812 1813 1814 1815 1816 1817 1818 1819 1820 1821 1822 1823 1824 1825 1826 1827 1828 1829 1830 1831 1832 1833 1834 1835 1836 1837 1838 1839 1840 1841 1842 1843 1844 1845 1846 1847 1848 1849 1850 1851 1852 1853 1854 1855 1856 1857 1858 1859 1860 1861 1862 1863 1864 1865 1866 1867 1868 1869 1870 1871 1872 1873 1874 1875 1876 1877 1878 1879 1880 1881 1882 1883 1884 1885 1886 1887 1888 1889 1890 1891 1892 1893 1894 1895 1896 1897 1898 1899 1900 1901 1902 1903 1904 1905 1906 1907 1908 1909 1910 1911 1912 1913 1914 1915 1916 1917 1918 1919 1920 1921 1922 1923 1924 1925 1926 1927 1928 1929 1930 1931 1932 1933 1934 1935 1936 1937 1938 1939 1940 1941 1942 1943 1944 1945 1946 1947 1948 1949 1950 1951 1952 1953 1954 1955 1956 1957 1958 1959 1960 1961 1962 1963 1964 1965 1966 1967 1968 1969 1970 1971 1972 1973 1974 1975 1976 1977 1978 1979 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010

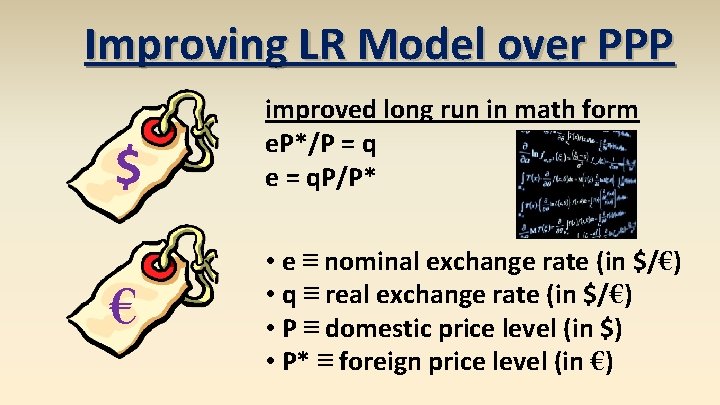
Improving LR Model over PPP $ If we relax PPP assumptions that don’t hold empirically, the following equation isn’t 1: e. P*/P = 1 € Instead: e. P*/P = q • q ≡ real exchange rate (in $/€)

Improving LR Model over PPP nominal exchange rate (e) – relative price of two currencies real exchange rate (q) – relative price of two output baskets (prices of a country’s goods and services relative to another country’s goods and services)

Improving LR Model over PPP $ € By the assumptions of PPP, the relative price of output baskets in two countries will equal their relative price levels (adjusted to the same currency), so q = 1. Introducing q makes the long run model more robust.

Improving LR Model over PPP $ € improved long run in math form e. P*/P = q e = q. P/P* • e ≡ nominal exchange rate (in $/€) • q ≡ real exchange rate (in $/€) • P ≡ domestic price level (in $) • P* ≡ foreign price level (in €)

Long Run Exchange Rate Long run determinates of e • relative price levels • trade barriers • imports vs. exports • productivity

Long Run Exchange Rate Factor Exchange Rate Domestic Currency domestic price level (P) ↑ e↑ depreciates foreign price level (P*) ↑ e↓ appreciates real exchange rate (q) ↑ e↑ depreciates trade barriers ↑ e↓ appreciates imports ↑ e↑ depreciates exports ↑ e↓ appreciates productivity ↑ e↓ appreciates

Long Run Exchange Rate Factor Exchange Rate Domestic Currency domestic MS ↑ e↑ depreciates foreign MS* ↑ e↓ appreciates domestic inflation (π) ↑ e↑ depreciates foreign inflation (π*) ↑ e↓ appreciates domestic output D ↑ e↓ appreciates foreign output D* ↑ e↑ depreciates domestic output S ↑ E? ambiguous foreign output S* ↑ E? ambiguous

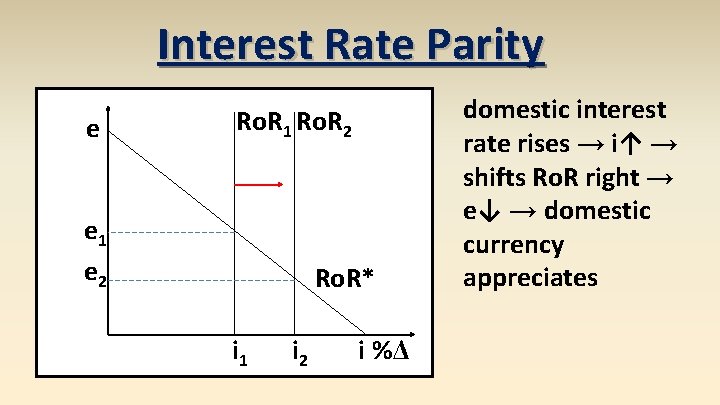
Interest Rate Parity There can be only one! interest rate parity – the rate of return should be the same throughout the world (assuming capital mobility) This is an arbitrage theory. If there are capital controls imposed, interest rate parity does not hold in the short run.

Interest Rate Parity IRP in math form Ro. R = (1 + i) Ro. R* = [E(et+1)/et](1 + i*) Ro. R = Ro. R* • Ro. R ≡ domestic rate of return • Ro. R* ≡ foreign rate of return • i ≡ domestic interest rate • i* ≡ foreign interest rate • E(et+1) ≡ expected future spot rate • et ≡ spot exchange rate

Interest Rate Parity Ro. R = (1 + i) Ro. R* = [E(et+1)/et](1 + i*) Ro. R = Ro. R* If you invest money domestically (at interest rate i), you should get the same return as investing money abroad (at interest rate i*) converting it initially at the spot rate and back at the expected future spot

Interest Rate Parity e Ro. R = (1 + i) Ro. R* = [E(et+1)/et](1 + i*) Ro. R = Ro. R* Ro. R e 1 Ro. R* i 1 i %Δ

Interest Rate Parity e Ro. R 1 Ro. R 2 e 1 e 2 Ro. R* i 1 i 2 i %Δ domestic interest rate rises → i↑ → shifts Ro. R right → e↓ → domestic currency appreciates

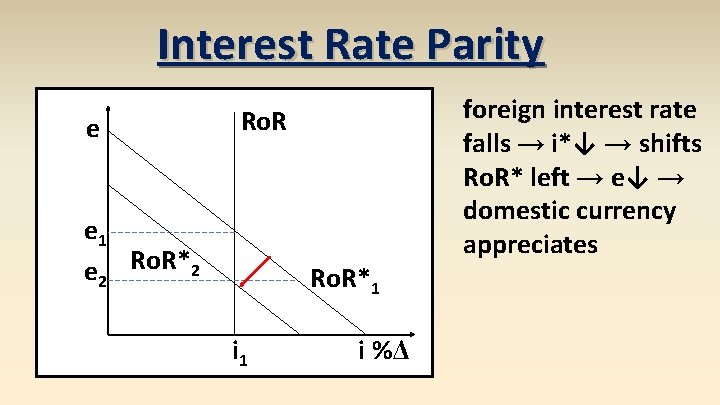
Interest Rate Parity e foreign interest rate falls → i*↓ → shifts Ro. R* left → e↓ → domestic currency appreciates Ro. R e 1 e 2 Ro. R*1 i %Δ

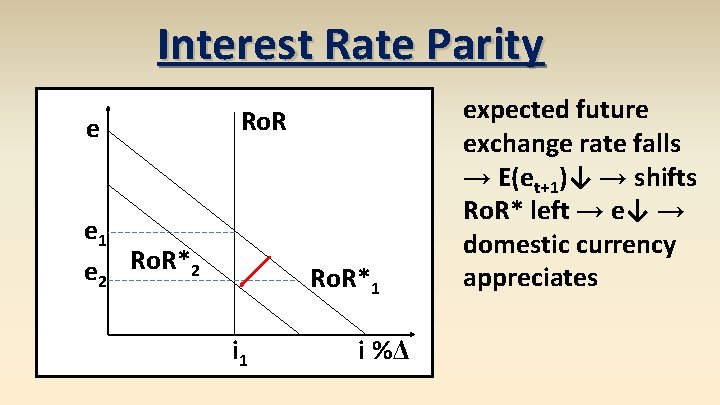
Interest Rate Parity e Ro. R e 1 e 2 Ro. R*1 i %Δ expected future exchange rate falls → E(et+1)↓ → shifts Ro. R* left → e↓ → domestic currency appreciates

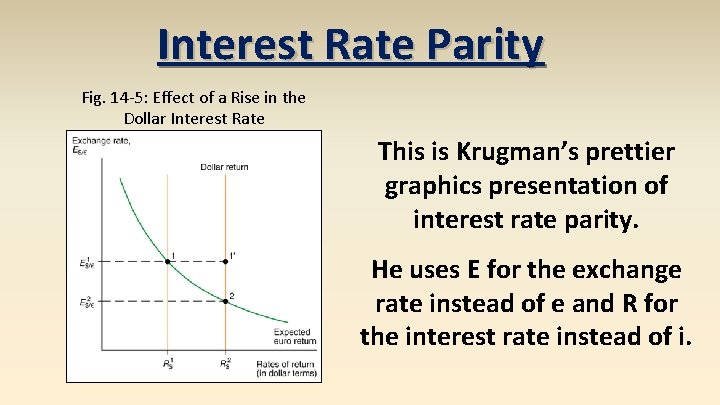
Interest Rate Parity Fig. 14 -5: Effect of a Rise in the Dollar Interest Rate This is Krugman’s prettier graphics presentation of interest rate parity. He uses E for the exchange rate instead of e and R for the interest rate instead of i.

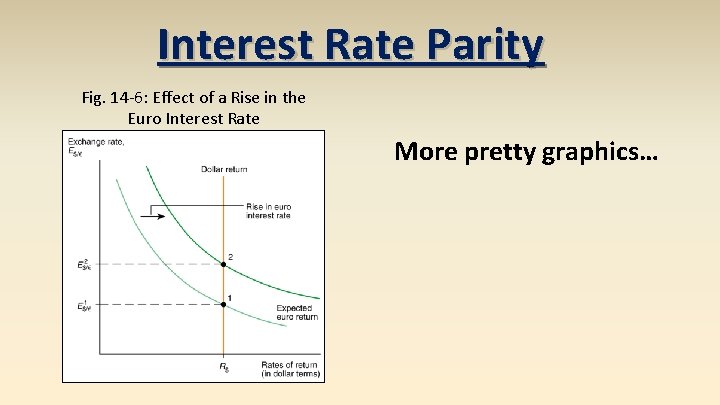
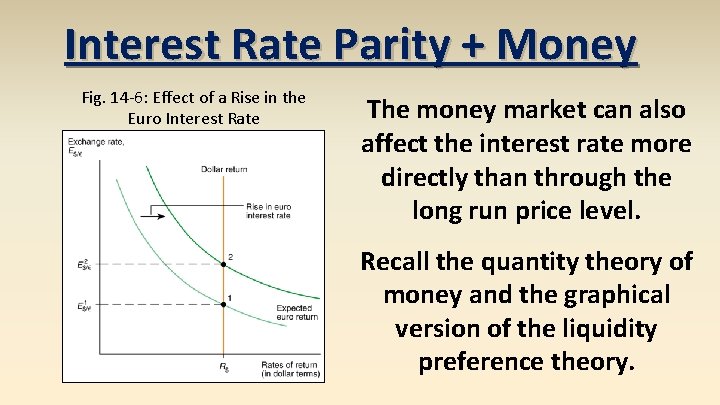
Interest Rate Parity Fig. 14 -6: Effect of a Rise in the Euro Interest Rate More pretty graphics…

Interest Rate Parity

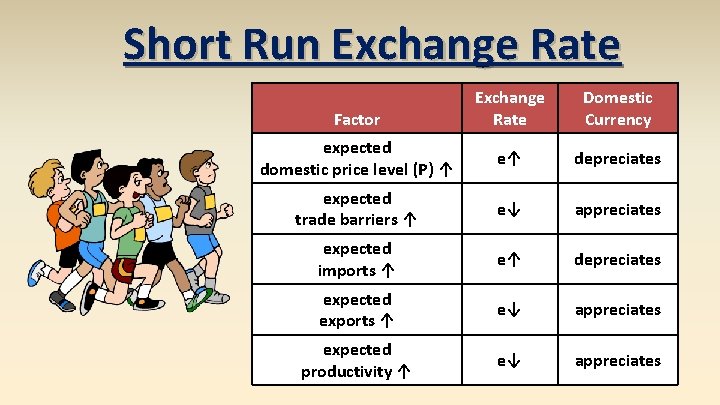
Short Run Exchange Rate Factor Exchange Rate Domestic Currency domestic interest (i) ↑ e↓ appreciates foreign interest rate (i*) ↑ e↑ depreciates expected future rate ↑ e↑ depreciates

Short Run Exchange Rate Because the expected future spot exchange rate impacts interest rate parity, all of the factors that effect the long run exchange rate enter into those expectations and can affect the short run exchange rate.

Short Run Exchange Rate Domestic Currency expected domestic price level (P) ↑ e↑ depreciates expected trade barriers ↑ e↓ appreciates expected imports ↑ e↑ depreciates expected exports ↑ e↓ appreciates expected productivity ↑ e↓ appreciates Factor

Interest Rate Parity + Money Fig. 14 -6: Effect of a Rise in the Euro Interest Rate The money market can also affect the interest rate more directly than through the long run price level. Recall the quantity theory of money and the graphical version of the liquidity preference theory.

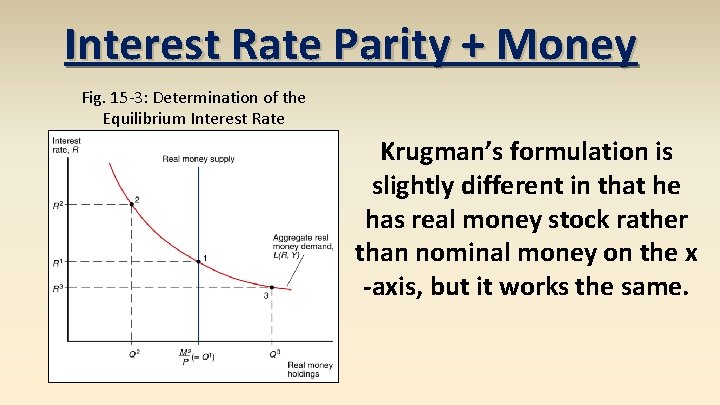
Interest Rate Parity + Money Fig. 15 -3: Determination of the Equilibrium Interest Rate Krugman’s formulation is slightly different in that he has real money stock rather than nominal money on the x -axis, but it works the same.

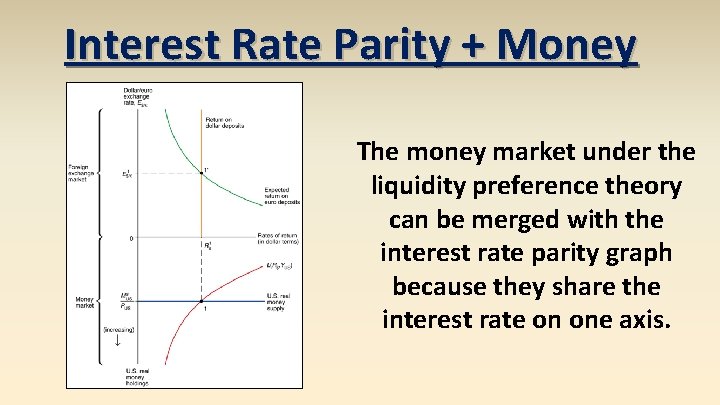
Interest Rate Parity + Money The money market under the liquidity preference theory can be merged with the interest rate parity graph because they share the interest rate on one axis.

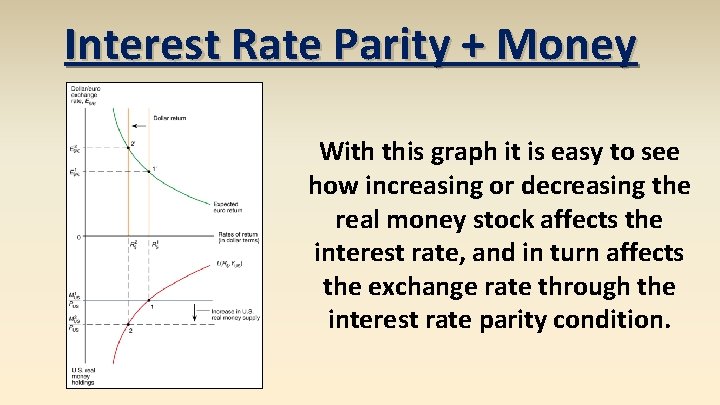
Interest Rate Parity + Money With this graph it is easy to see how increasing or decreasing the real money stock affects the interest rate, and in turn affects the exchange rate through the interest rate parity condition.

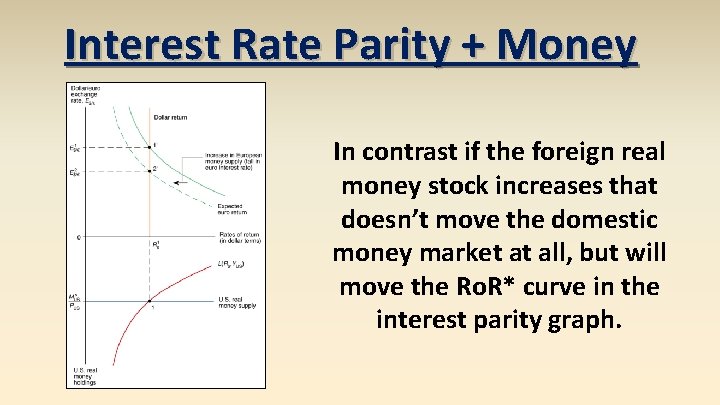
Interest Rate Parity + Money In contrast if the foreign real money stock increases that doesn’t move the domestic money market at all, but will move the Ro. R* curve in the interest parity graph.

Short Run Exchange Rate Factor Exchange Rate Domestic Currency domestic MS/P ↑ e↑ depreciates foreign MS*/P* ↑ e↓ appreciates

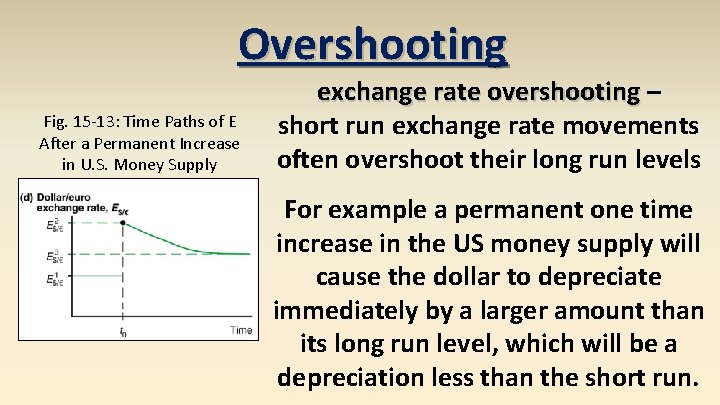
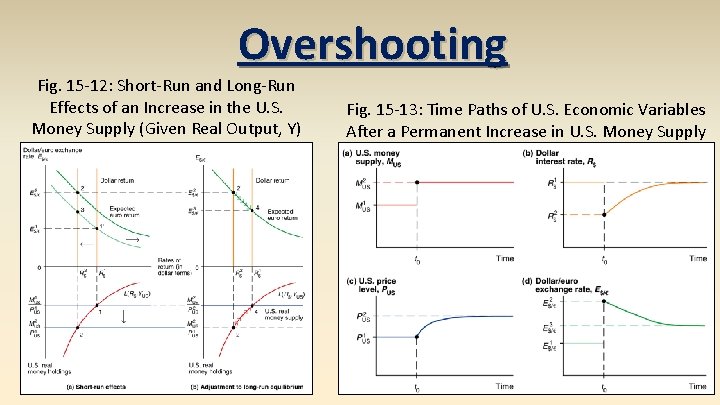
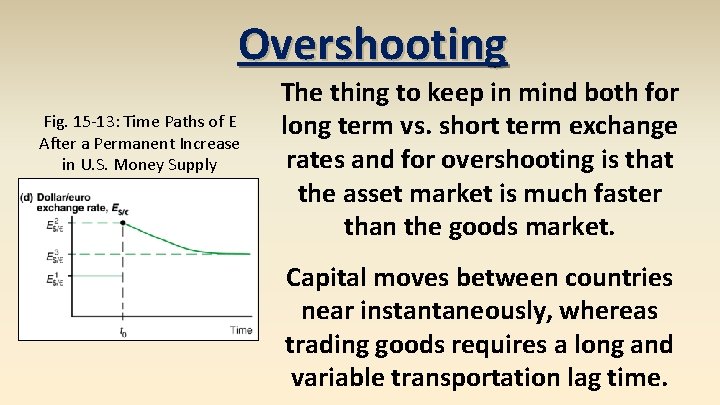
Overshooting Fig. 15 -13: Time Paths of E After a Permanent Increase in U. S. Money Supply exchange rate overshooting – short run exchange rate movements often overshoot their long run levels For example a permanent one time increase in the US money supply will cause the dollar to depreciate immediately by a larger amount than its long run level, which will be a depreciation less than the short run.

Overshooting Fig. 15 -12: Short-Run and Long-Run Effects of an Increase in the U. S. Money Supply (Given Real Output, Y) Fig. 15 -13: Time Paths of U. S. Economic Variables After a Permanent Increase in U. S. Money Supply

Overshooting Fig. 15 -13: Time Paths of E After a Permanent Increase in U. S. Money Supply The thing to keep in mind both for long term vs. short term exchange rates and for overshooting is that the asset market is much faster than the goods market. Capital moves between countries near instantaneously, whereas trading goods requires a long and variable transportation lag time.

Short Run Exchange Rate Krugman uses short run exchange rate fluctuations as an excuse to introduce Keynesianism. We will talk about Keynesian theories (the Mundell-Fleming Model), but for our purposes interest rate parity drives the short run e and PPP drives the long run e.