Unit 3 Energy Part 2 Energy Transfer Chapter

Unit 3 Energy Part 2 Energy Transfer Chapter 15: Thermochemistry

• Heat – energy transferred from an object at high temperature to one at a lower temperature – Also known as enthalpy or ΔH for change • Law of conservation of energy – energy is neither created nor destroyed. Only transferred!

• SI Unit for Enthalpy is Joules (J) – 1000 joules (J) = 1 kilojoule (k. J) • calorie (cal) – the amount of energy required to raise the temperature of one gram of pure water by one degree Celsius – in nutrition we use Calories • 1000 calories = 1 Calorie = 1 kcal

Specific Heat • The amount of heat required to raise the temperature of one gram of that substance by one degree Celsius. – Specific heat of water = 4. 184 J/(g • °C) • You should KNOW this number

Calculating Heat q = m x c x ∆T heat absorbed or released (J) mass of sample specific heat change in temperature (g) (J/g • °C) (°C)

The sign of q or H - Exothermic Processes • energy is produced • heat OR enthalpy is negative OR • Hand warmers + Endothermic Processes • energy is absorbed • heat OR enthalpy is positive OR • Ice packs

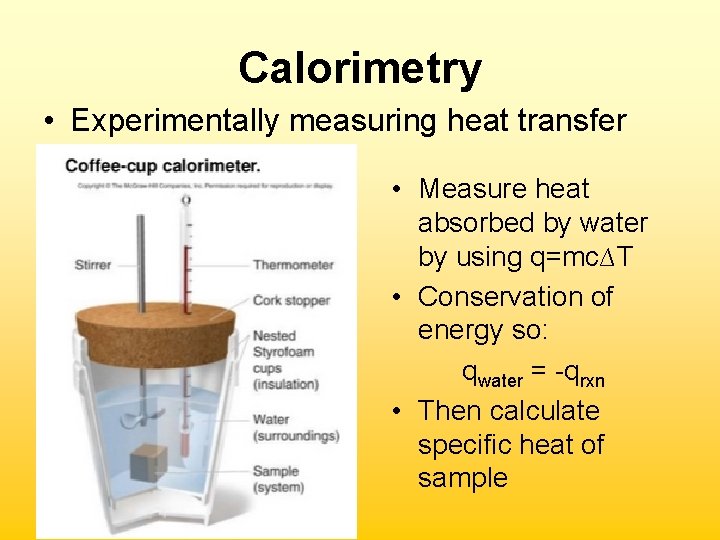
Calorimetry • Experimentally measuring heat transfer • Measure heat absorbed by water by using q=mc∆T • Conservation of energy so: qwater = -qrxn • Then calculate specific heat of sample

Example Problem The temperature of a sample of iron with a mass of 10. 0 g changed from 50. 4°C to 25. 0°C with the release of 114 J. What is the specific heat of iron? q = -114 joules c = ? m = 10. 0 g ∆T = 25. 0°C - 50. 4°C = -25. 4°C

q = m x c x ∆T q c = m x ∆T c = -114 J 10. 0 g x -25. 4°C = 0. 449 J/g • °C

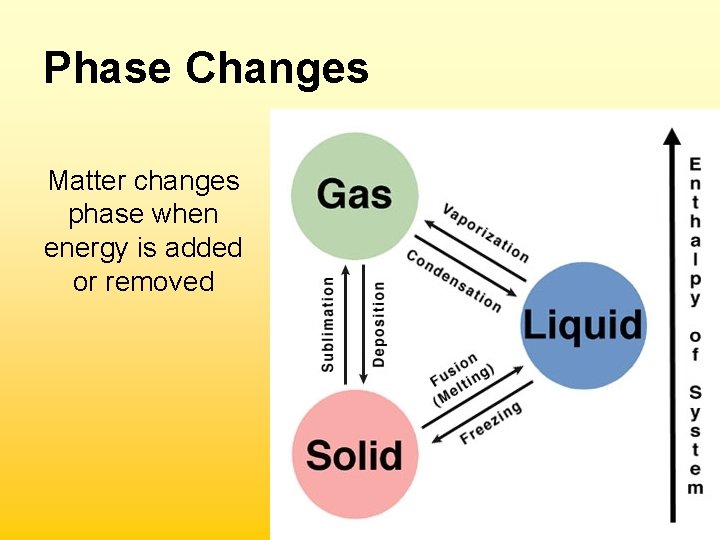
Phase Changes Matter changes phase when energy is added or removed

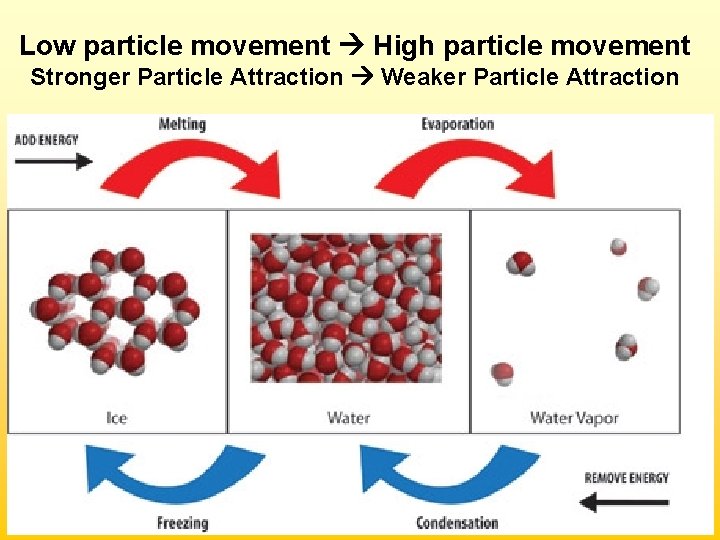
Low particle movement High particle movement Stronger Particle Attraction Weaker Particle Attraction

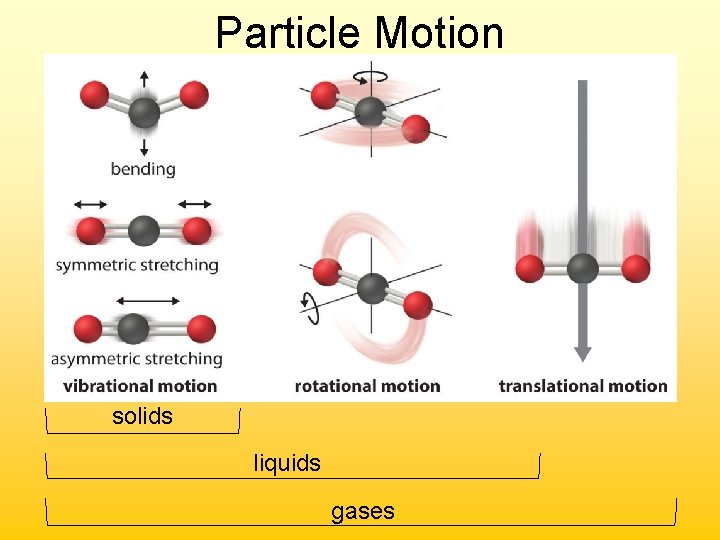
Particle Motion solids liquids gases

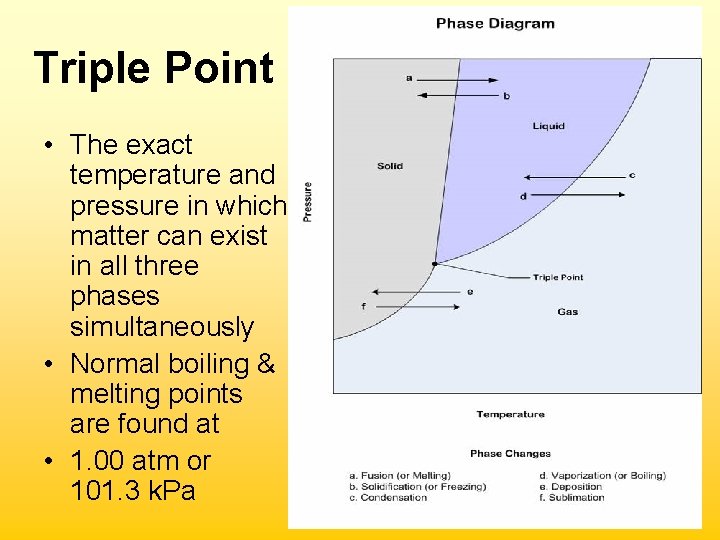
Triple Point • The exact temperature and pressure in which matter can exist in all three phases simultaneously • Normal boiling & melting points are found at • 1. 00 atm or 101. 3 k. Pa

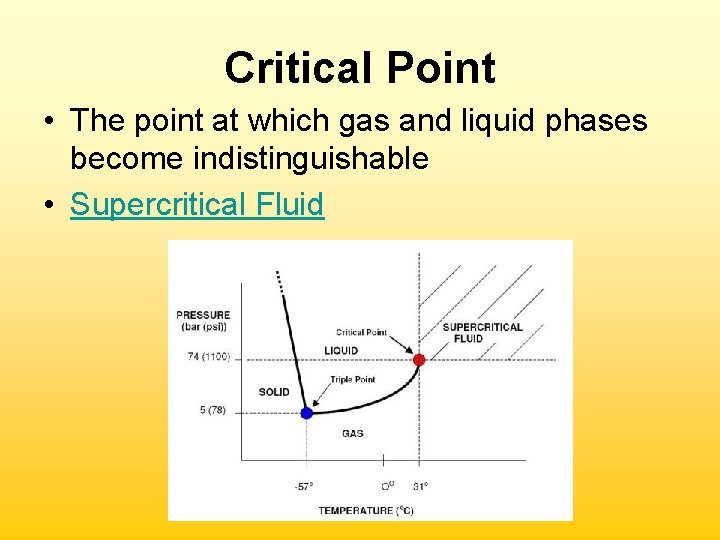
Critical Point • The point at which gas and liquid phases become indistinguishable • Supercritical Fluid

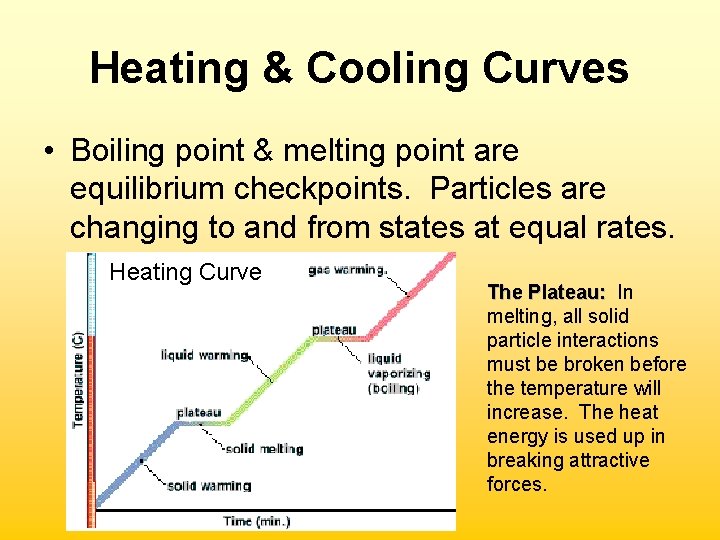
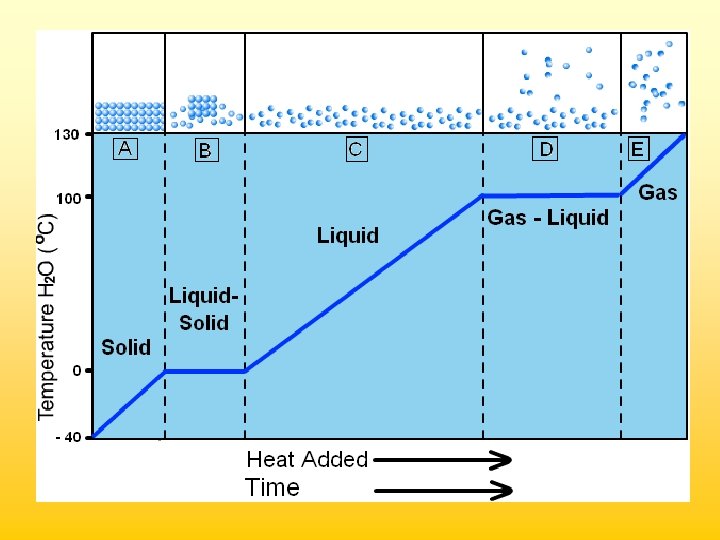
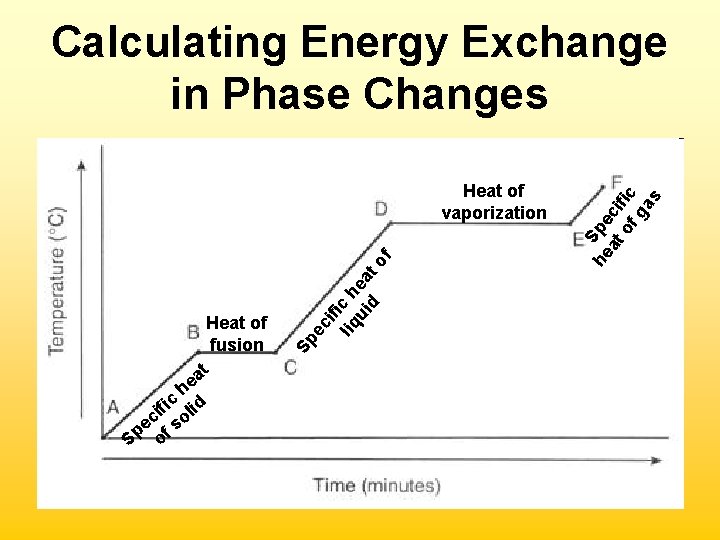
Heating & Cooling Curves • Boiling point & melting point are equilibrium checkpoints. Particles are changing to and from states at equal rates. Heating Curve The Plateau: In melting, all solid particle interactions must be broken before the temperature will increase. The heat energy is used up in breaking attractive forces.

Heat of Fusion/Vaporization • Measured in k. J/mol (J/mol) • ∆Hfusion = energy required to completely melt a solid • ∆Hvaporization = energy required to completely vaporize a liquid • Change the signs to find energy released when liquid freezes/gas condenses

he fic lid i ec f so p S o Sp ec Heat of fusion at ifi liq c h ui ea d to f Heat of vaporization he Spe at ci of fic ga s Calculating Energy Exchange in Phase Changes

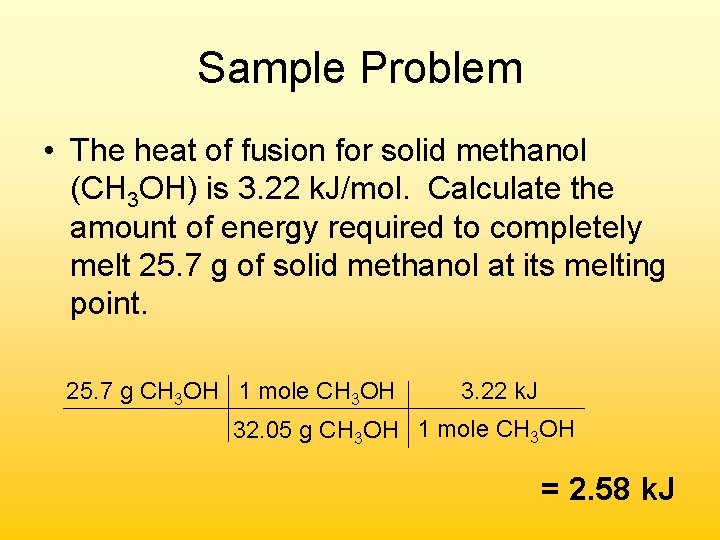
Sample Problem • The heat of fusion for solid methanol (CH 3 OH) is 3. 22 k. J/mol. Calculate the amount of energy required to completely melt 25. 7 g of solid methanol at its melting point. 25. 7 g CH 3 OH 1 mole CH 3 OH 3. 22 k. J 32. 05 g CH 3 OH 1 mole CH 3 OH = 2. 58 k. J

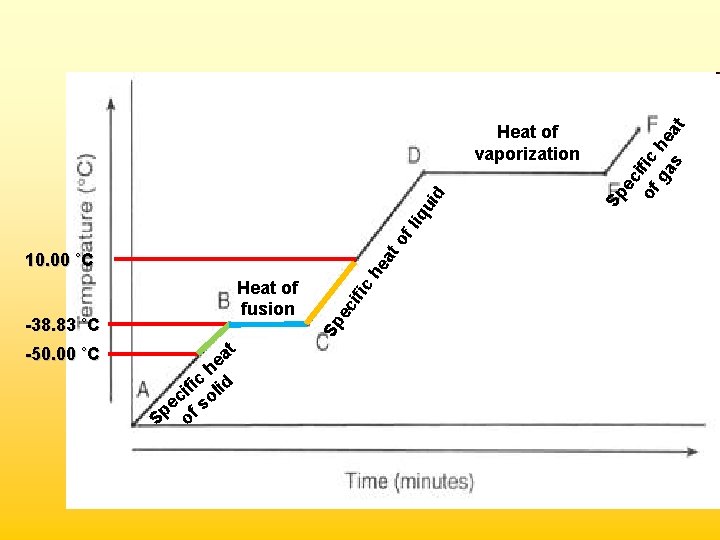
Sample Problem • Given the following information for mercury (Hg) below, calculate the total amount of energy required when 45. 0 g of mercury at -50. 00˚C is heated to 10. 00˚C. State of Matter Solid Liquid Gas Phase Change Melting Boiling Temperature (˚C) -38. 83 356. 7 Specific Heat (J/g • ˚C) 0. 14 1. 25 1. 04 Phase Change Fusion Vaporization Molar Heat (k. J/mol) 2. 32 5. 92

of -50. 00 ˚C t a e h c ifi olid c e fs p S o c ifi ec -38. 83 ˚C Sp Heat of fusion he at 10. 00 ˚C Sp ec of ific ga he s at liq ui d Heat of vaporization

• Segment 1 – Solid warming (specific heat) q = mc∆T = (45. 0 g)(0. 14 J/g˚C)(11. 17˚C) = 70. J • Segment 2 – Solid melting (heat of fusion) 45. 0 g Hg 1 mole Hg 2320 J Hg 200. 59 g Hg 1 mole Hg = 520. J • Segment 3 – Liquid warming (specific heat) q = mc∆T = (45. 0 g)(1. 25 J/g˚C)(48. 83˚C) = 2, 750 J Total Energy Required: = 70. J + 520. J + 2750 J = 3, 340 J

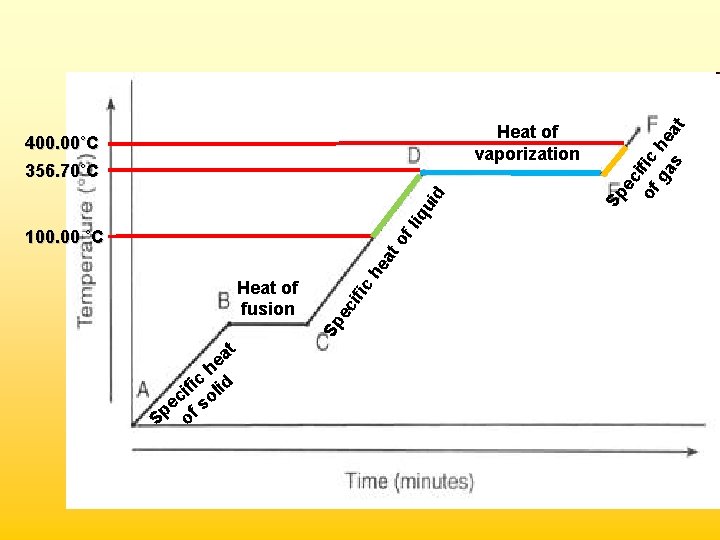
Practice Problem • Given the following information for mercury (Hg) below, calculate the total amount of energy required when 15. 0 g of mercury at 100. 00˚C is heated to 400. 00˚C. State of Matter Solid Liquid Gas Phase Change Melting Boiling Temperature (˚C) -38. 83 356. 70 Specific Heat (J/g • ˚C) 0. 14 1. 25 1. 04 Phase Change Fusion Vaporization Molar Heat (k. J/mol) 2. 32 5. 92

d liq ui t a e h c ifi olid c e fs p S o c ifi ec Sp Heat of fusion he at of 100. 00 ˚C Sp ec of ific ga he s at Heat of vaporization 400. 00˚C 356. 70˚C

• Segment 1 – Liquid warming (specific heat) q = mc∆T = (15. 0 g)(1. 25 J/g˚C)(256. 70˚C) = 4, 810 J • Segment 2 – Liquid Boiling (heat of vap) 15. 0 g Hg 1 mole Hg 5920 J Hg 200. 59 g Hg 1 mole Hg = 443 J • Segment 3 – Gas warming (specific heat) q = mc∆T = (15. 0 g)(1. 04 J/g˚C)(43. 30˚C) = 675 J Total Energy Required: = 4, 810 J + 443 J + 675 J = 5, 930 J

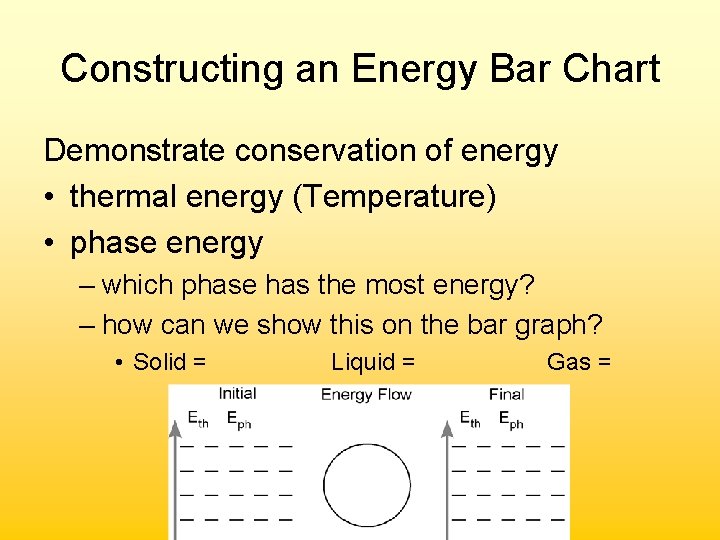
Constructing an Energy Bar Chart Demonstrate conservation of energy • thermal energy (Temperature) • phase energy – which phase has the most energy? – how can we show this on the bar graph? • Solid = Liquid = Gas =

Assign values to Eph • Due to interactions between particles, the energy stored due to the arrangement of particles is ranked: solids < liquids < gases • We choose to represent these phases by using: – Solids = 1 bar – Liquids = 2 bars – Gases = 4 bars

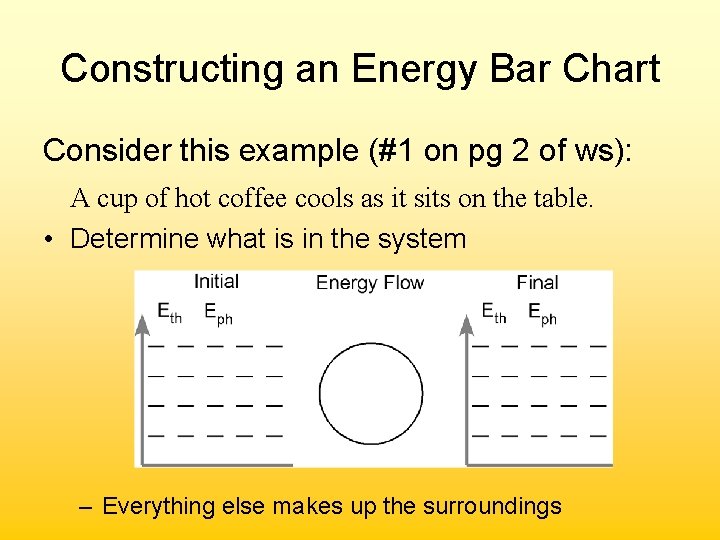
Constructing an Energy Bar Chart Consider this example (#1 on pg 2 of ws): A cup of hot coffee cools as it sits on the table. • Determine what is in the system cup coffee – Everything else makes up the surroundings

Assign values to Eph • Use two Eph bars before and after cup coffee

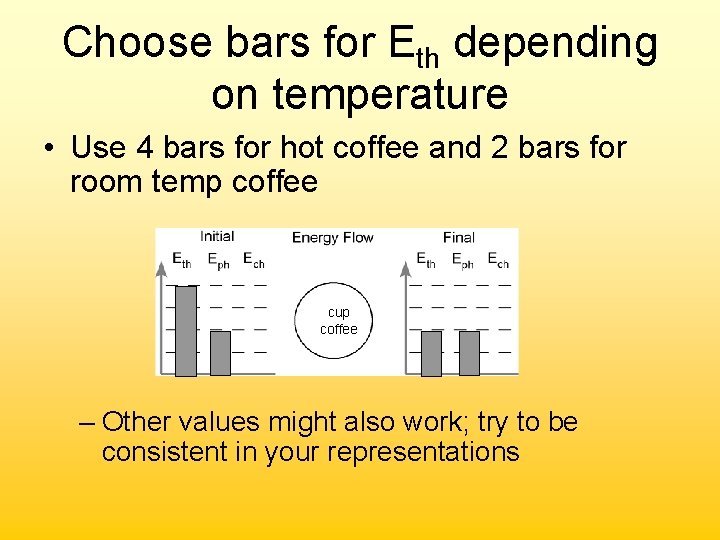
Choose bars for Eth depending on temperature • Use 4 bars for hot coffee and 2 bars for room temp coffee cup coffee – Other values might also work; try to be consistent in your representations

Now show energy transfer • Final situation has 2 less bars of E than initial; 2 bars had to leave the system

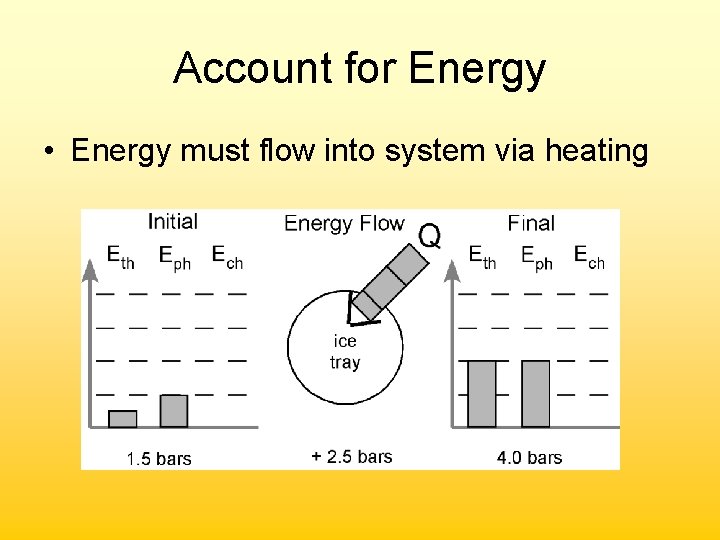
Now, consider phase change • • A tray of ice cubes (-8 ˚C) is placed on the counter and becomes water at room temperature What do we know about the situation? – – – • What is the system? The Eph (increases or decreases). How do you know? The Eth (increases or decreases). How do you know? Now represent these changes in bar graph.

Account for Energy • Energy must flow into system via heating