UNIT 3 APPORTIONMENT FAIR DIVISION 3 3 APPLICATIONS

Use the Huntington-Hill principle to allocate objects other than representatives. Helpful Tip: Once

Preventing the Alabama paradox from occurring Minimizing the relative unfairness between any two companies

USING HUNTINGTON-HILL TO ASSIGN POLICE OFFICERS Suppose a small town has seven police officers.

ANOTHER EXAMPLE… You are to allocate thirteen buses to four routes of a regional

Slides: 5

Download presentation

UNIT 3 – APPORTIONMENT & FAIR DIVISION 3. 3 APPLICATIONS OF THE APPORTIONMENT PRINCIPLE

Use the Huntington-Hill principle to allocate objects other than representatives. Helpful Tip: Once you have used the largest of the Huntington-Hill numbers to apportion a representative, cross that number off so you do NOT use it again. 2/13/2022 9. 3 APPLICATIONS OF THE APPORTIONMENT PRINCIPLE

Preventing the Alabama paradox from occurring Minimizing the relative unfairness between any two companies Note: The relative unfairness between two states CANNOT be improved if apportionment is done as described by the Huntington-Hill principle This is the current method used to apportion Congress today, though it is not flawless Note: The Huntington-Hill principle can violate the quota rule 2/13/2022 TWO IMPORTANT CRITERIA

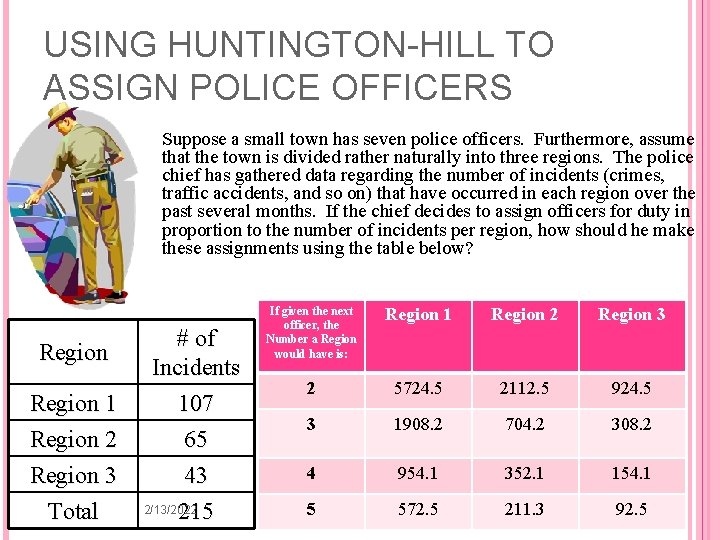
USING HUNTINGTON-HILL TO ASSIGN POLICE OFFICERS Suppose a small town has seven police officers. Furthermore, assume that the town is divided rather naturally into three regions. The police chief has gathered data regarding the number of incidents (crimes, traffic accidents, and so on) that have occurred in each region over the past several months. If the chief decides to assign officers for duty in proportion to the number of incidents per region, how should he make these assignments using the table below? Region 1 Region 2 Region 3 Total # of Incidents 107 65 43 2/13/2022 215 If given the next officer, the Number a Region would have is: Region 1 Region 2 Region 3 2 5724. 5 2112. 5 924. 5 3 1908. 2 704. 2 308. 2 4 954. 1 352. 1 154. 1 5 572. 5 211. 3 92. 5

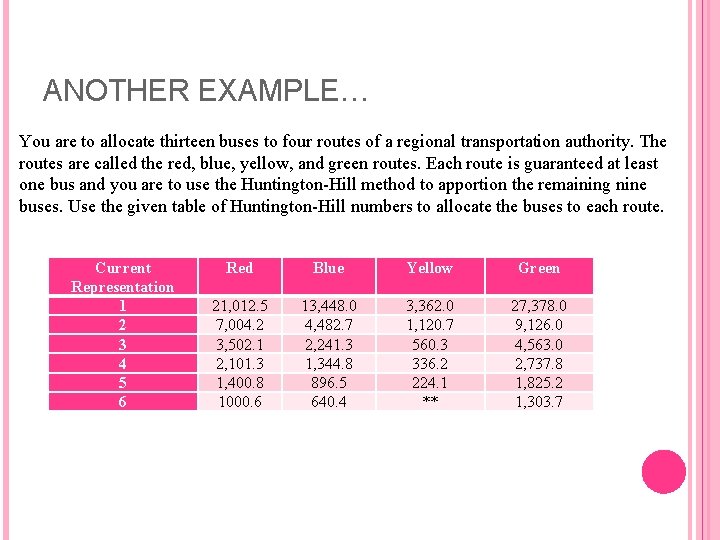
ANOTHER EXAMPLE… You are to allocate thirteen buses to four routes of a regional transportation authority. The routes are called the red, blue, yellow, and green routes. Each route is guaranteed at least one bus and you are to use the Huntington-Hill method to apportion the remaining nine buses. Use the given table of Huntington-Hill numbers to allocate the buses to each route. Current Representation 1 2 3 4 5 6 Red Blue Yellow Green 21, 012. 5 7, 004. 2 3, 502. 1 2, 101. 3 1, 400. 8 1000. 6 13, 448. 0 4, 482. 7 2, 241. 3 1, 344. 8 896. 5 640. 4 3, 362. 0 1, 120. 7 560. 3 336. 2 224. 1 ** 27, 378. 0 9, 126. 0 4, 563. 0 2, 737. 8 1, 825. 2 1, 303. 7