Unit 21 ANGULAR GEOMETRIC PRINCIPLES 1 NAMING ANGLES

Unit 21 ANGULAR GEOMETRIC PRINCIPLES 1

NAMING ANGLES n n Angles are named by a number, a letter, or three letters For example, the angle shown can be called 1, B, ABC, or CBA A B 1 C n n When an angle is named with three letters, the vertex must be the middle letter. In cases where a point is the vertex of more than one angle, a single letter cannot be used to name an angle 2

TYPES OF ANGLES n n n An acute angle is an angle that is less than 90° A right angle is an angle of 90° An obtuse angle is an angle greater than 90° and less than 180° A straight angle is an angle of 180° A reflex angle is an angle greater than 180° and less than 360° Two angles are adjacent if they have a common vertex and a common side 3

ANGLES FORMED BY A TRANSVERSAL n Transversal: A line that intersects (cuts) n n two or more lines. Alternate interior angles: Pairs of interior angles on opposite sides of the transversal and have different vertices. Corresponding angles: Pairs of angles, one interior and one exterior, located on same side of the transversal, but with different vertices. 4

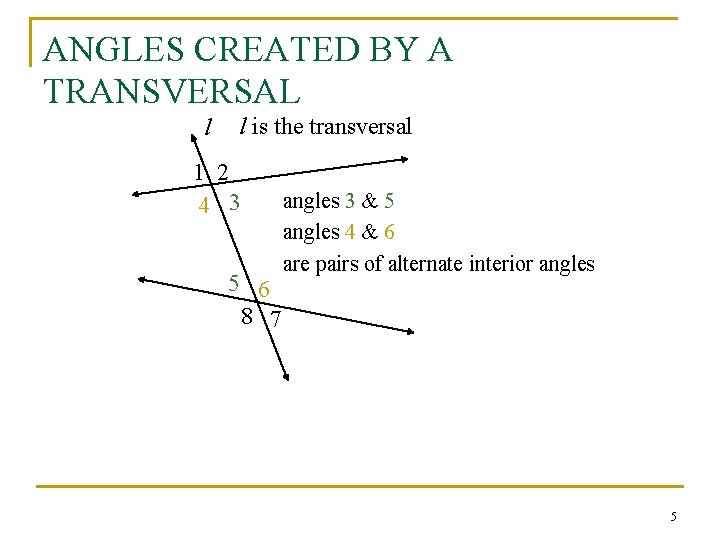
ANGLES CREATED BY A TRANSVERSAL l l is the transversal 1 2 4 3 5 6 8 7 angles 3 & 5 angles 4 & 6 are pairs of alternate interior angles 5

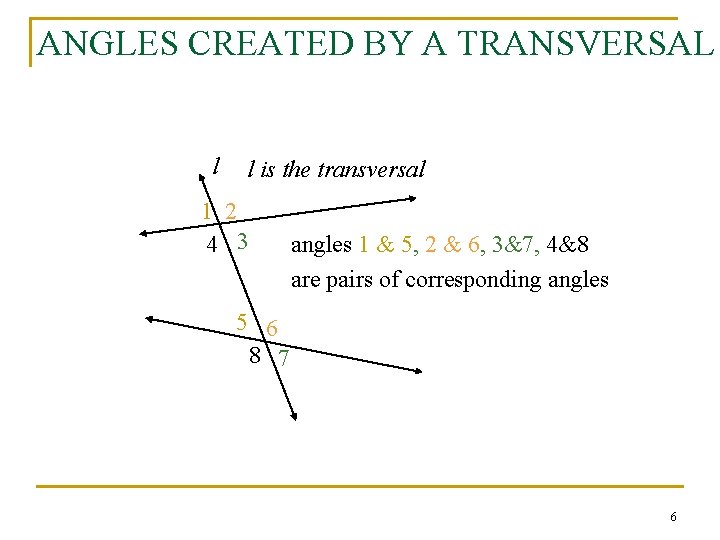
ANGLES CREATED BY A TRANSVERSAL l l is the transversal 1 2 4 3 angles 1 & 5, 2 & 6, 3&7, 4&8 are pairs of corresponding angles 5 6 8 7 6

THEOREMS AND COROLLARIES n n A theorem is a statement in geometry that can be proved. A corollary is a statement based on a theorem. q A corollary is often a special case of a theorem 7

THEOREMS AND COROLLARIES (Cont) n The following are theorems and corollaries used throughout the text. They are numbered for easier reference (follow in your book for a visual) 1. 2. 3. If two lines intersect, the opposite, or vertical angles are equal. If two parallel lines are intersected by a transversal, the alternate interior angles are equal If two lines are intersected by a transversal and a pair of alternate interior angles are equal, the lines are parallel. 8

THEOREMS AND COROLLARIES (Cont) 4. 5. 6. 7. If two parallel lines are intersected by a transversal, the corresponding angles are equal If two lines are intersected by a transversal and a pair of corresponding angles are equal, the lines are parallel Two angles are either equal or supplementary if their corresponding sides are perpendicular 9

ANGULAR MEASURE EXAMPLE • Determine the measure of all the missing angles in the figure below given that l m, p q, 1 = 110°, and 2 = 80°: 1 5 3 l m q 4 6 2 • 3 = 110 because it is vertical to 1 (Theorem #1) • 4 = 110 because it is alternate interior to 3 (Theorem #2) and corresponding to 1 (Theorem #4) 8 p • 5 = 70 (180° – 110°) because it is supplementary to both 1 and 3 10

ANGULAR MEASURE EXAMPLE • Determine the measure of all the missing angles in the figure below given that l m, p q, 1 = 110°, and 2 = 80°: 1 5 3 l m q 4 6 2 8 p • 6 = 70 because it is corresponding to 5 (Theorem #4) • 8 = 2 = 80 because two angles are either equal or supplementary if their corresponding sides are parallel (Theorem #6) 11

PRACTICE PROBLEMS Define the terms in problems 1– 6: n 1. 2. 3. 4. 5. 6. Obtuse angle Reflex angle Corresponding angles Transversal Straight angle Name 1 in the figure below in three C additional ways: D 1 E 12

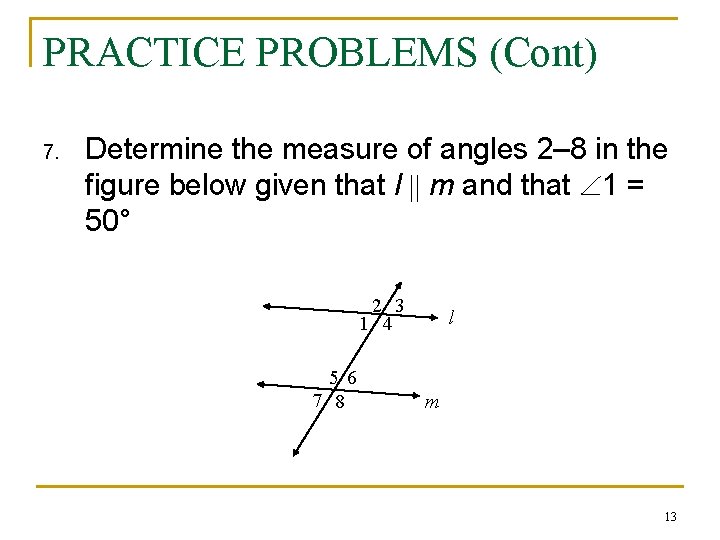
PRACTICE PROBLEMS (Cont) 7. Determine the measure of angles 2– 8 in the figure below given that l m and that 1 = 50° 2 3 1 4 5 6 7 8 l m 13

PROBLEM ANSWER KEY 1. 2. 3. 4. 5. 6. 7. An angle greater than 90 and less than 180 An angle greater than 180° and less than 360° A pair of angles, one interior and one exterior. Both angles are on the same side of the transversal with different vertices A line that intersects (cuts) two or more lines An angle of 180° D, CDE, EDC 2 = 130 , 3 = 50 , 4 = 130 , 5 = 130 , 6 = 50 , 7 = 50 , and 8 = 130 14