Unit 20 ANGULAR MEASURE 1 TERMS DEFINED l

Unit 20 ANGULAR MEASURE 1

TERMS DEFINED l l l An angle is a figure made by two lines that intersect An angle is also described as the union of two rays having a common end point The two rays are called the sides of the angle, and their common end point is called a vertex Angles are measured in degrees. The degree symbol is °; the angle symbol is The degree of precision required in measuring and computing angles depends on how the angle is used A complete circle equals 360° 2

UNITS OF ANGULAR MEASURE The decimal degree is generally the preferred unit of measurement in metric calculations l In the United States it is customary to express angular measure in the following ways: l l As decimal degrees, such as 9. 7 degrees As fractional degrees, such as 36 1/2 degrees As degrees, minutes, and seconds, such as 63 degrees, 27 minutes, 48 seconds A degree is divided in 60 equal parts called minutes ( ) l A minute is divided in 60 equal parts called seconds ( ) l So we now have a conversion between degrees, minutes and seconds l 3

Converting to decimal degrees EXPRESSING DEGREES, can use unity fraction method or dimensional analysis like in units 8 &AS 9 MINUTES, AND SECONDS l Start with the. DEGREES seconds and convert to DECIMAL l We minutes. l Then convert the minutes into degrees and add the decimal onto your degrees. 4

CONVERSION EXAMPLE l Express 73° 57 48 as decimal degrees: l l Convert the 48 to minutes Add that to your minutes l l So 57. 8’ Now change that to degrees Add to the 73° So 73. 963° 5

CONVERSION EXAMPLE Express 48. 54 as degrees, minutes, and seconds (DMS): l You know you have the 48° already so you can work with the decimal. l l Convert the decimal to minutes l l So we have 32’ Now convert that decimal minutes to seconds l So 48° 32’ 24” 6

ADDING ANGLES • Add the following angles: 49° 53 37 + 38 47 24 Add seconds to seconds, minutes to minutes, etc. 87° 100 61 – Simplify the sum: 61 = 1 1 – Now add the 1 to the 100 or 100 + 1 = 101 – Change 101 to degrees: 101 = 1 41 – Add the 1 degree to the 87 degrees and combine all the units: 87 + 1 = 88 , so we end up with 88 41 1 Ans 7

Converting on Calculators l Scientific calculators will do the tedious work with DMS and decimal degrees. The easiest way to find how to do it is to refer to your manual or google DMS and you calculator model. I am fairly familiar with all the calculators out there so if you have trouble please get a hold of me. I will explain some of the commonly used calculators in class. 8

• Subtract the following angles: SUBTRACTING ANGLES 89 23 15 – 70 35 20 – – – 20 cannot be subtracted from 15 , so borrow 60 from the 23 35 cannot be subtracted from the 22 that were left after borrowing, so borrow 60 from the 89 Complete the subtraction 88 82 75 – 70 35 20 18 47 55 Ans 9

MULTIPLYING ANGLES • Multiply 51 33 42 by 3: 51 33 42 3 153° 99 126 – Simplify the product 126 = 2 6 – Adding these 2 to the 99 , we now have 101 = 1 41 – Adding this degree to the 153 degrees, we now have 154° – Combining units, we now have 154 41 6 Ans 10

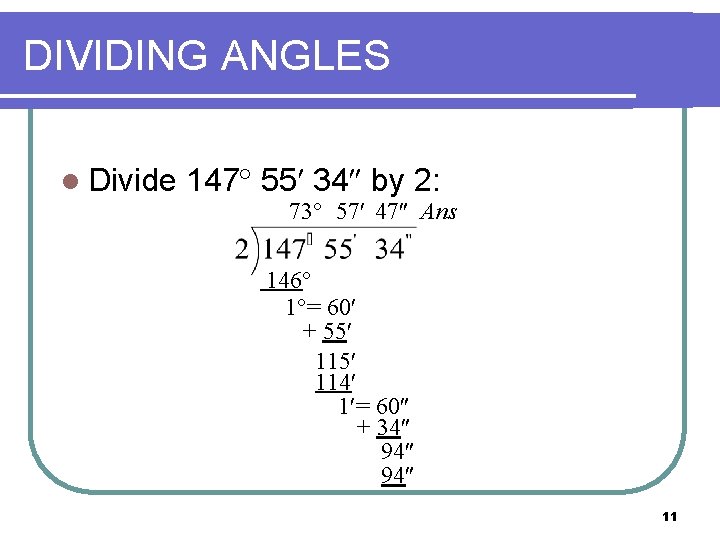
DIVIDING ANGLES l Divide 147 55 34 by 2: 73 57 47 Ans 146 1°= 60 + 55 114 1 = 60 + 34 94 94 11

Two angles are complementary COMPLEMENTS AND when their sum is 90° SUPPLEMENTS l Two angles are supplementary when their sum is 180° l Determine the complement of 43° 18 : l l Subtract 43 18 from 90 (or 89 60 ) to find its complement 89 60 – 43 18 46 42 Ans 12

PRACTICE PROBLEMS l Express the following degrees, minutes, and seconds as decimal degrees. Round to three decimal places where necessary: 1. 2. l Express the following decimal degrees as degrees, minutes, and seconds: 3. 4. l 143 54 32 242 33 24 129. 76° 85. 845° Perform the following operations. Simplify all answers: 5. 6. 45° 54 39 + 79 17 43 87 16 25 – 76 21 36 13

PRACTICE PROBLEMS (Cont) 54 47 32 + 16 19 35 8. 72 15 15 – 60 20 20 9. 43 33 29 3 10. 54 48 15 3 11. 136 58 45 4 12. 272 38 52 4 13. Determine the complement of 49 15 16 14. Determine the supplement of 49 15 16 15. Determine the supplement of 147 36 21 7. 14

PROBLEM ANSWER KEY 1. 2. 3. 4. 5. 6. 7. 8. 143. 909° 242. 557° 129 45 36 85 50 42 125 12 22 10 54 49 71 7 7 11 54 55 130 40 27 10. 18 16 5 11. 547 55 0 12. 68 9 43 13. 40 44 44 14. 130 44 44 15. 32° 23 39 9. 15