UNIT 2 Properties of DFT Circular Convolution 692021

UNIT 2 Properties of DFT & Circular Convolution 6/9/2021

TOPICS COVERED • linearity • Time shift & Frequency shift • circular convolution • parsevals theorem • correlation • Even and odd sequences 6/9/2021

UNIT-2 Properties of DFT: 1. Circular shift xn is a length N sequence defined for n = 0, 1, …N-1. An arbitrary shift applied to xn will knock it out of the 0…N-1 range. Therefore, a circular shift that always keeps the shifted sequence in the range 0…N-1 is defined using a modulo operation: (1) (2) 6/9/2021

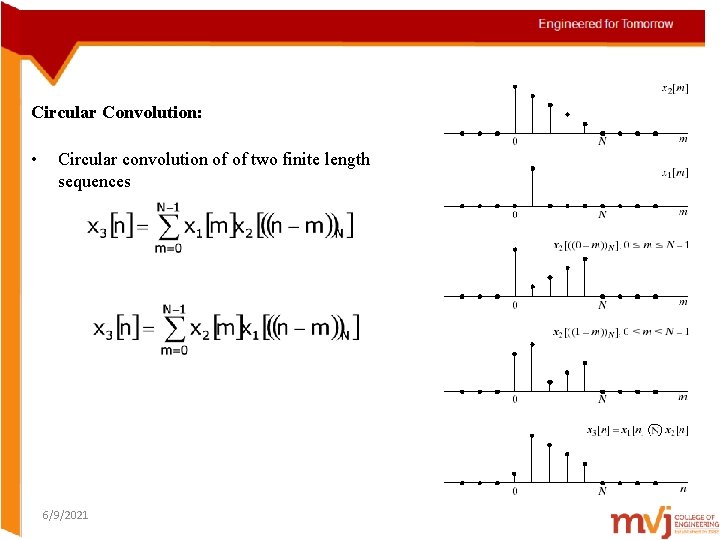
2. Circular convolution A linear convolution for two length N sequences xn and gn has a length 2 N-1: (3) A circular convolution is a length-N sequence defined as: N N (4) (5) Procedure: take two sequences of the same length (zero-pad if needed), DFT of them, multiply, IDFT: a circular convolution. 6/9/2021

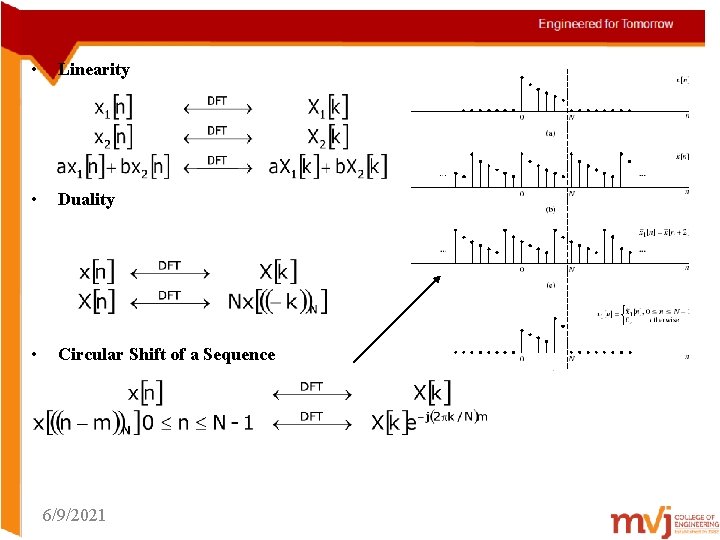
• Linearity • Duality • Circular Shift of a Sequence 6/9/2021

Example: Duality Circular Convolution: • Circular convolution of of two finite length sequences 6/9/2021

• Example: Circular convolution of two rectangular pulses L=N=6 • DFT of each sequence • Multiplication of DFTs • And the inverse DFT 6/9/2021

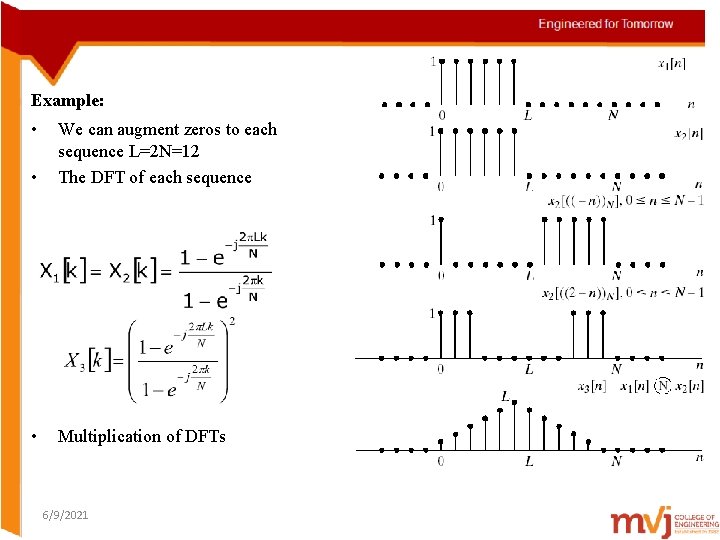
Example: • • We can augment zeros to each sequence L=2 N=12 The DFT of each sequence • Multiplication of DFTs 6/9/2021

Example: (1) Take N frequency samples of (1) and then IDFT: (2) aliased version of xn The results of circular convolution differ from the linear convolution “on the edges” – caused by aliasing. To avoid aliasing, we need to use zero-padding… 6/9/2021

DFT properties: General Btw, g[n] = gn 6/9/2021

DFT properties: Symmetry xn is a real sequence 6/9/2021

DFT properties: Symmetry (cont) xn is a complex sequence 6/9/2021

N-point DFTs of 2 real sequences via a single N-point DFT Let gn and hn are two length N real sequences. Form xn = gn + jhn Xk (1) (2) (3) (4) 6/9/2021