Unit 2 Polynomial and Rational Functions Pre Calculus

Unit 2 Polynomial and Rational Functions Pre. Calculus 2 -R

Find the maximum value of the function. f (x) = – 4 x 2 + 48 x – 50 f (6) = 94 Find the maximum value of the function. g(x) = 7 x 2 – 28 x 1 f (2) = – 28 Review Problems

Find the domain and range of the function. f (x) = x 2 – 12 x + 2 D=( ), R = [– 34, ) If a ball is thrown directly upward with a velocity of 80 ft/s, its height (in feet) after t seconds is given by y = 80 t – 16 t 2. What is the maximum height attained by the ball? 100 feet 2 Review Problems

A manufacturer finds that the revenue generated by selling x units of a certain commodity is given by the function R (x) = 192 x – 0. 4 x 2 where the revenue R (x) is measured in dollars. What is the maximum revenue, and how many units should be manufactured to obtain this maximum? $23, 040, 240 units 3 Review Problems

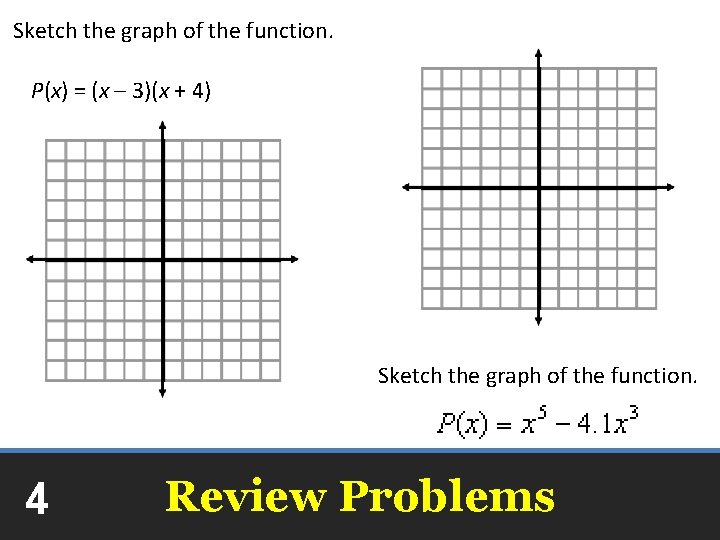
Sketch the graph of the function. P(x) = (x – 3)(x + 4) Sketch the graph of the function. 4 Review Problems

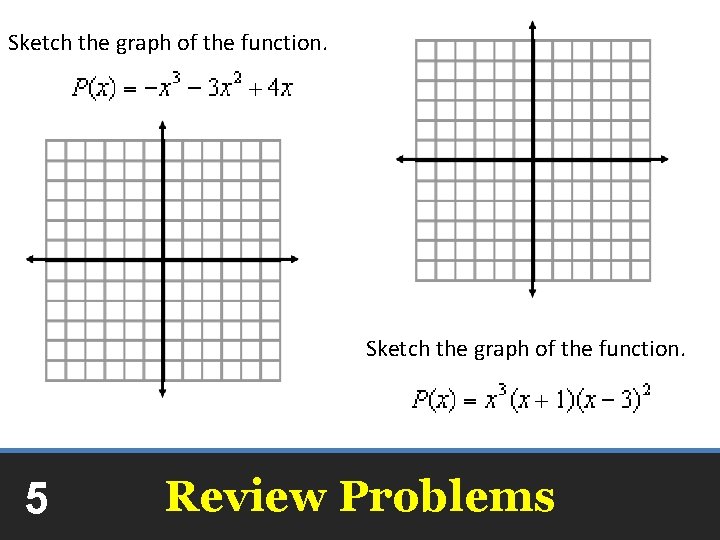
Sketch the graph of the function. 5 Review Problems

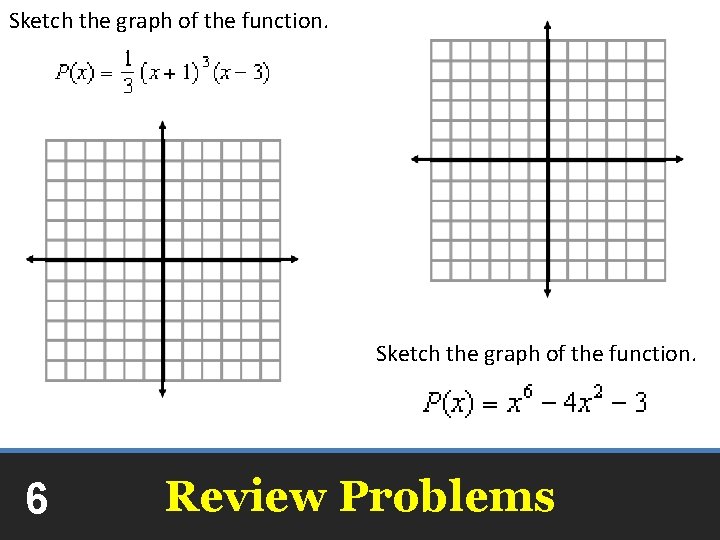
Sketch the graph of the function. 6 Review Problems

Find the coordinates of all local extrema of the function. y = x 3 – 12 x + 6 x = 2, y = – 10, and x = – 2, y = 22 Find the coordinates of all local extrema of the function. y = x 4 – 4 x 3 x = 0, y = 0, and x = 3, y = – 27 7 Review Problems

How many local maxima and minima does the polynomial have? y = x 4 – 4 x 2 + 4 1 maximum and 2 minima How many local maxima and minima does the polynomial have? y = 0. 2 x 5 + 2 x 4 – 11. 67 x 3 – 66 x 2 + 160 x + 5 2 maximum and 2 minima 8 Review Problems

Find the quotient and remainder using division. The quotient is (x + 1); the remainder is – 38. Find the quotient and remainder using division. The quotient is 1; the remainder is (2 x + 3). 9 Review Problems

Find the quotient and remainder using division. The quotient is the remainder is 5 10 Review Problems ;

Evaluate P(3) for: 38 Evaluate P(2) for: 234 11 Review Problems

Evaluate for: Use the Factor Theorem to choose a factor of 12 Review Problems

Find a polynomial of degree 5 and zeros of – 6, – 2, 0, 2, and 6 Find a polynomial of degree 3 that has zeros of 2, – 4, and where the coefficient of x 2 is 6. 13 Review Problems

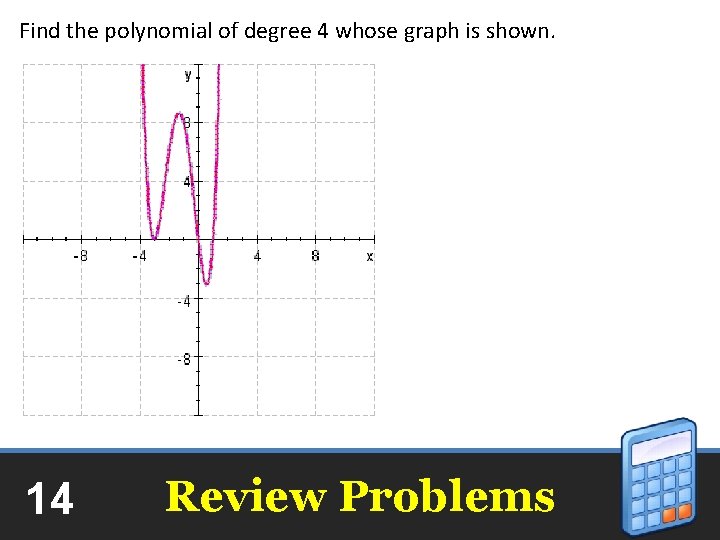
Find the polynomial of degree 4 whose graph is shown. 14 Review Problems

List all possible rational zeros given by the Rational Zeros Theorem (but don't check to see which actually are zeros). Use Descartes' Rule of Signs to determine how many positive and how many negative real zeros the polynomial can have. Then determine the possible total number of real zeros. 0, 2 or 4 negative 15 Review Problems

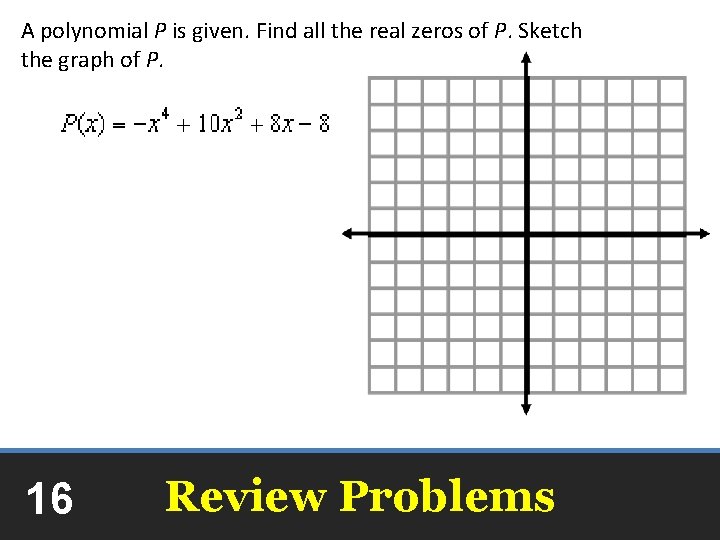
A polynomial P is given. Find all the real zeros of P. Sketch the graph of P. 16 Review Problems

Find all rational zeros of the polynomial. 17 Review Problems

Find all rational zeros of the polynomial. 18 Review Problems

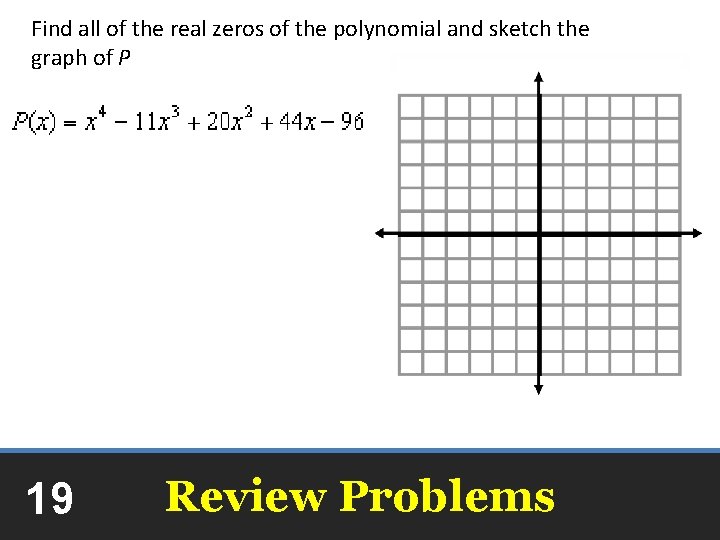
Find all of the real zeros of the polynomial and sketch the graph of P 19 Review Problems

Evaluate the expression (9 + 14 i) + (7 – 11 i) and write the result in the form a + bi. 16 + 3 i Evaluate the expression 10(– 2 + 14 i) and write the result in the form a + bi. – 20 + 140 i 20 Review Problems

Evaluate the expression and write the result in the form a + bi. 16 + 8 i Evaluate the expression and write the result in the form a + bi. 21 2 – 15 i Review Problems

Evaluate the expression i 17 and write the result in the form a + bi. i Evaluate the expression and write the result in the form a + bi. 2 i 22 Review Problems

Evaluate the expression and write the result in the form a + bi. – 18 Find all solutions of the equation x 2 – 8 x + 25 = 0 and express them in the form a + bi. x = 4 + 3 i, x = 4 – 3 i 23 Review Problems

Find all solutions of the equation and express them in the form a + bi. z = – 4 + 2 i, z = – 4 – 2 i A polynomial P is given. Factor P completely. 24 Review Problems

Find the polynomial P(x) of degree 3 with integer coefficients, and zeros 4 and 3 i. Factor the polynomial completely and find all its zeros. 25 Review Problems

Factor the polynomial completely into linear factors with complex coefficients Find the x- and y-intercepts of the rational function x-intercept (6, 0), y-intercept (0, – 1) 26 Review Problems

Find the x- and y-intercepts of the rational function x-intercept (– 3, 0), y-intercept (0, 3) Find the horizontal and vertical asymptotes of the rational function horizontal asymptote y = 0; vertical asymptote x = – 8 27 Review Problems

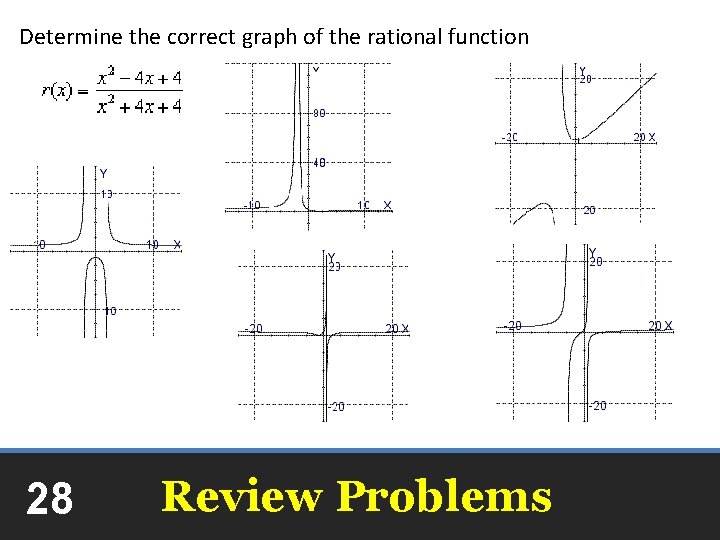
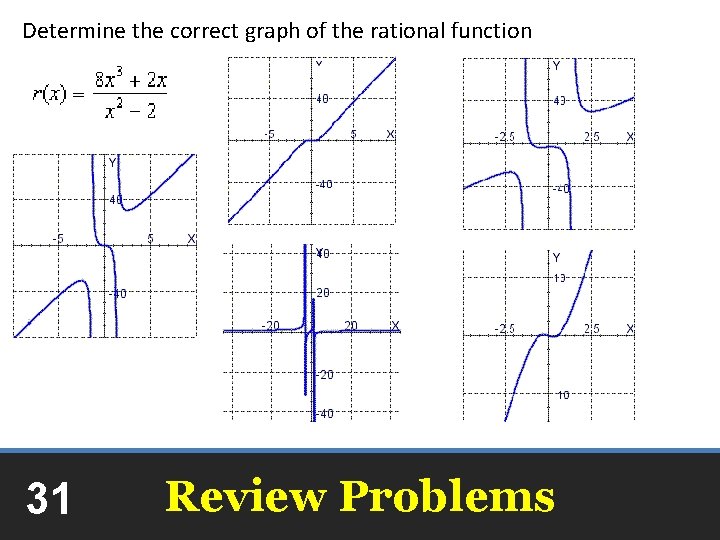
Determine the correct graph of the rational function 28 Review Problems

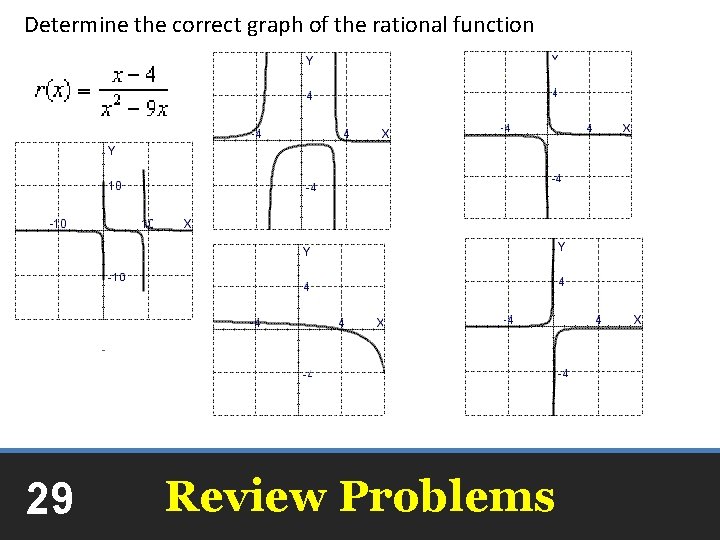
Determine the correct graph of the rational function 29 Review Problems

Find the slant asymptote of the function y=x+4 30 Review Problems

Determine the correct graph of the rational function 31 Review Problems

Use a Graphing Calculator to find vertical asymptotes, x- and yintercepts, and local extrema, correct to the nearest decimal. (a) Find all vertical asymptotes. x = 2 (b) Find x-intercept(s). (c) Find y-intercept(s). x=0 y=0 (d) Find the local minimum. (e) Find the local maximum. 32 (2. 7, 12. 3) none Review Problems

Find the intercepts and asymptotes (a) Determine the x-intercept(s). no solution (b) Determine the y-intercept(s). y = – 3 (c) Determine the vertical asymptote(s). (d) Determine the horizontal asymptote(s). 33 x = – 1, x = 3 y=3 Review Problems

Find all horizontal and vertical asymptotes (if any). (a) Find all horizontal asymptotes (if any). (b) Find all vertical asymptotes (if any). no solution x = 2, x = – 2 34 Review Problems

Find the intercepts and asymptotes (a) Determine the x-intercept(s). x=2 (b) Determine the y-intercept(s). y = – 1 (c) Determine the vertical asymptote(s). x = – 8 (d) Determine the horizontal asymptote(s). y = 4 35 Review Problems

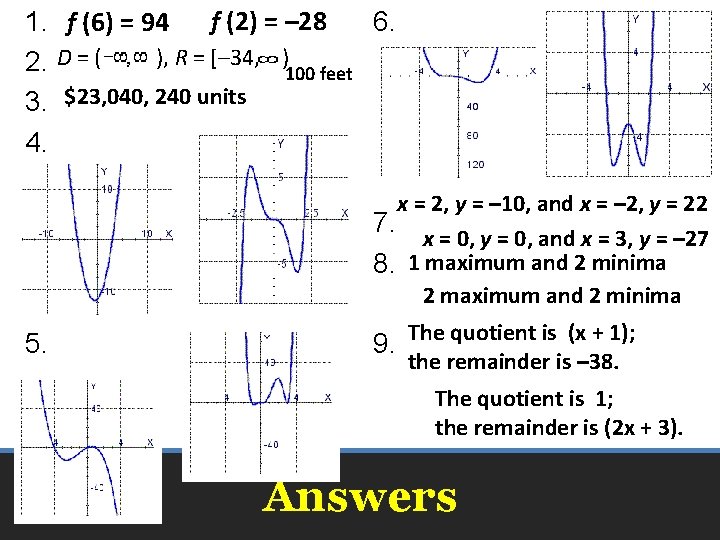
1. f (6) = 94 f (2) = – 28 6. ), R = [– 34, ) 2. D = ( 100 feet 3. $23, 040, 240 units 4. x = 2, y = – 10, and x = – 2, y = 22 7. x = 0, y = 0, and x = 3, y = – 27 8. 1 maximum and 2 minima 2 maximum and 2 minima 5. The quotient is (x + 1); 9. the remainder is – 38. The quotient is 1; the remainder is (2 x + 3). Answers

10. The quotient is the remainder is 5 11. 38 12. 13. 14. 15. 16. ; 17. 18. 19. 234 0, 2 or 4 negative 16 + 3 i 20. – 20 + 140 i 21. 16 + 8 i 2 – 15 i 22. i 2 i 23. – 18 x = 4 + 3 i, x = 4 – 3 i 24. z = – 4 + 2 i, z = – 4 – 2 i Answers

25. 26. 27. 28. 29. 30. 31. 32. x-intercept (6, 0), y-intercept (0, – 1) x-intercept (– 3, 0), y-intercept (0, 3) horizontal asymptote y = 0; vertical asymptote x = – 8 33. no solution x = – 1, x = 3 y = – 3 y=3 34. no solution x = 2, x = – 2 35. x =y 2= – 1 x y= =– 84 a c y=x+4 c x=2 x=0 y=0 (2. 7, 12. 3) none Answers