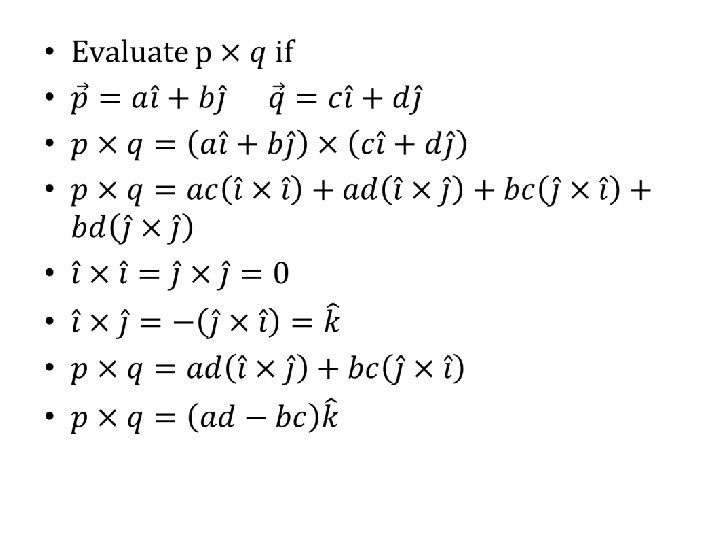Unit 2 Newtons Laws Newtons Laws of Motion


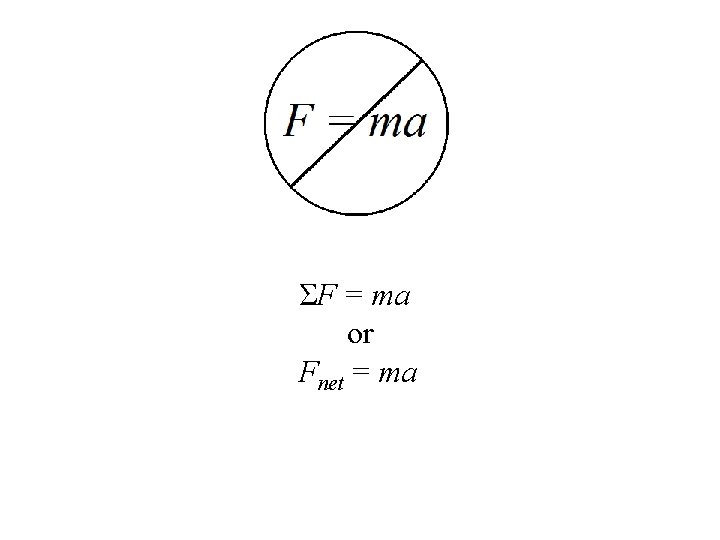
















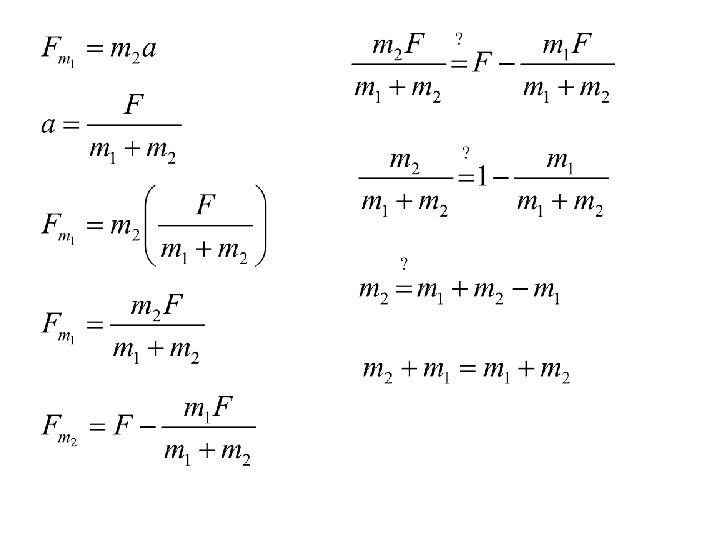











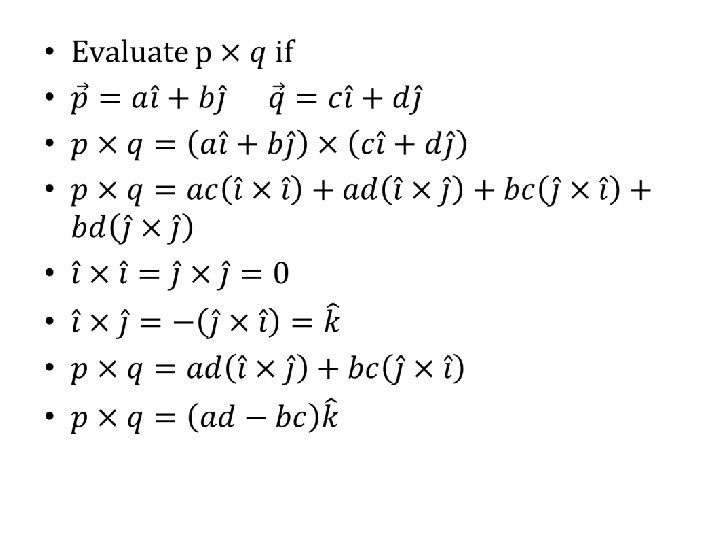
- Slides: 42

Unit 2 Newton’s Laws

• Newton’s Laws of Motion 1) Law of inertia: An object will remain in its current state of motion unless acted upon by an external force. 2) ΣF = ma 3) For every action (force) there is an equal and opposite reaction (force). (Forces always come in pairs!)
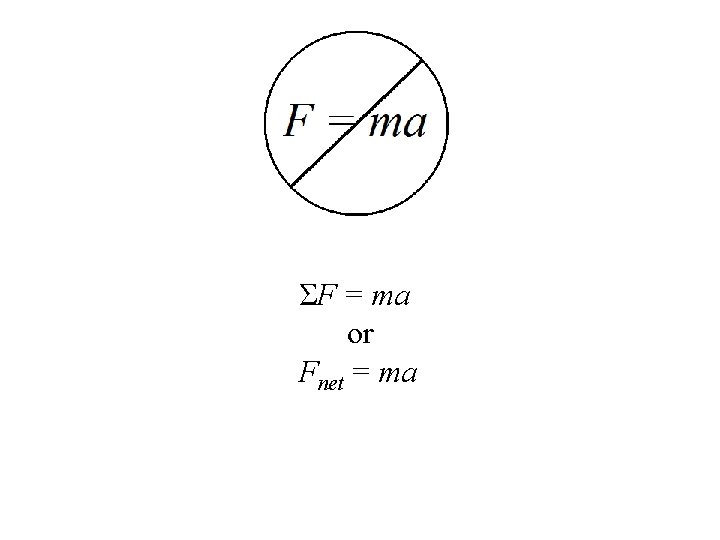
ΣF = ma or Fnet = ma

• Types of forces 1) Field a) Gravity b) Electromagnetic 2) Contact a) b) c) d) e) Tension Normal Friction Applied Resistance

• Gravity • Fg = mg • Also known as “weight”

• Tension • T = mg for a suspended mass • T < mg for a falling mass • T > mg for a mass accelerating upward

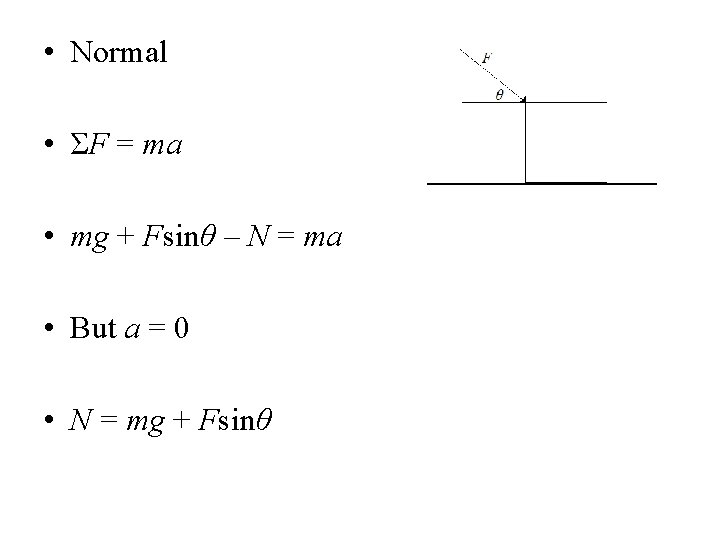
• Normal means perpendicular • N = mg on a horizontal surface* • N = mgcosθ on a slope of angle θ* • *Applied forces that are not parallel to the surface will affect the normal force

• Normal • ΣF = ma • mg + Fsinθ – N = ma • But a = 0 • N = mg + Fsinθ

• Friction • f = μN • When two surfaces slide relative to each other it is kinetic friction μk • When two surfaces are stationary relative to each other it is static friction μs • μ is almost always less than 1 • For a given pair of surfaces, μk < μs

• Applied • Any external push or pull not already covered

• Resistance • Usually air or water resistance • A VERY common topic for differential equations

• A ball falls and is subject to a resistance force FR = –bv. Develop an equation for the velocity of the ball as a function of time. At t = 0, v = 0

• A ball falls and is subject to a resistance force FR = –bv. Develop an equation for the velocity of the ball as a function of time. At t = 0, v = 0

• Terminal velocity • Constant velocity of a falling object • What would be the terminal velocity in the previous example?

• A ball falls and is subject to a resistance force FR = –bv. Develop an equation for the velocity of the ball as a function of time. At t = 0, v = 0

• Free Body Diagrams • They show all external forces acting on an object • A vector represents each force. – The head points in the direction of the force – The tail begins at the point of origin of the force – The length of the vector should be representative of the magnitude of the force – When asked to draw a free body diagram on a test, include only forces, not components – Label appropriately, using symbols from the problem

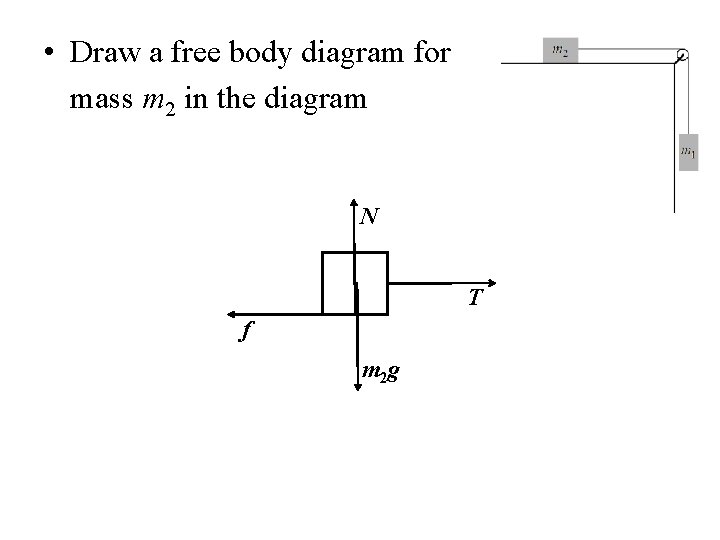
• Draw a free body diagram for mass m 2 in the diagram N T f m 2 g

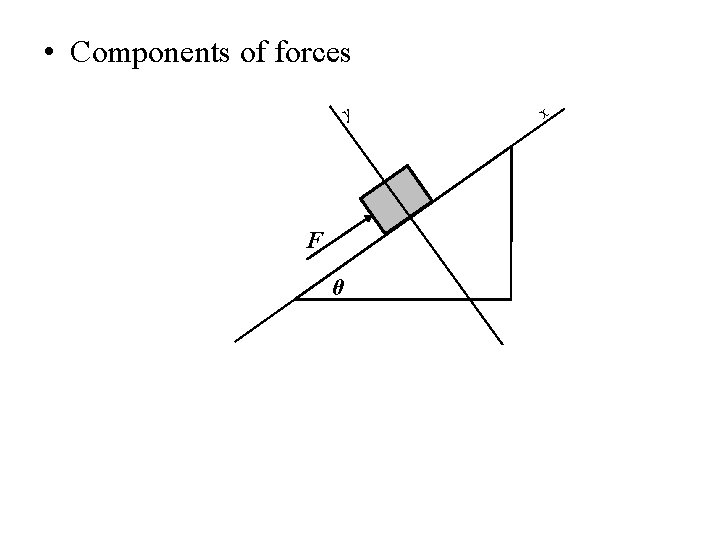
• Components of forces • Always chose a coordinate system to minimize components

• Components of forces y F θ x

• Components of forces N f sθ co θ mg F mg m in gs θ


• Applications of Newton’s third law F m 1 m 2 • Determine the force of m 2 on m 1 a
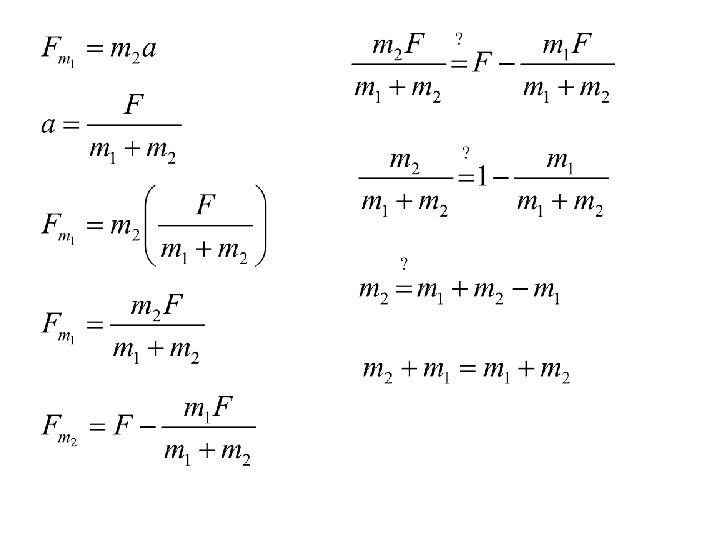


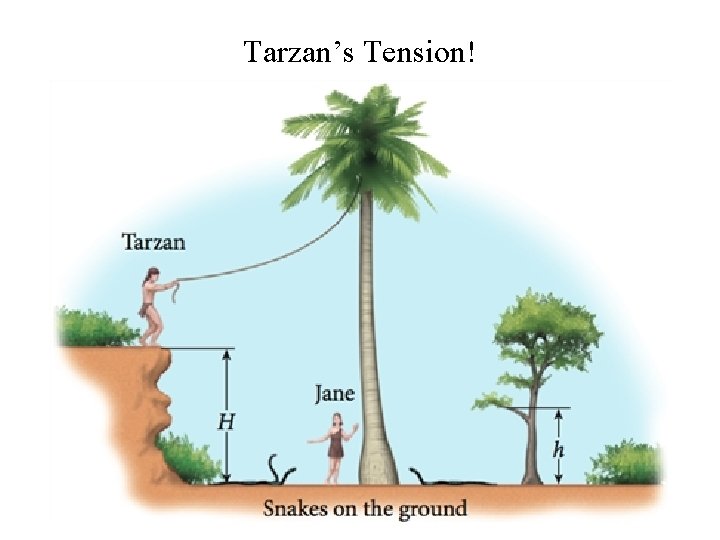
Tarzan’s Tension!

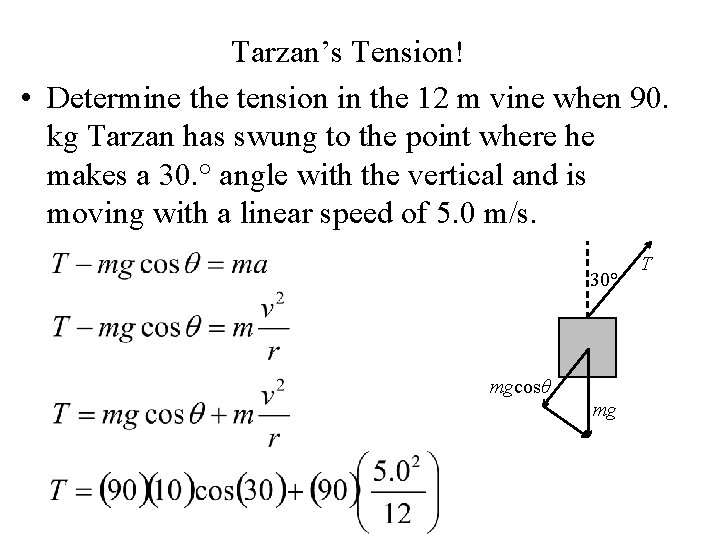
Tarzan’s Tension! • Determine the tension in the 12 m vine when 90. kg Tarzan has swung to the point where he makes a 30. ° angle with the vertical and is moving with a linear speed of 5. 0 m/s. 30° mgcosθ mg T


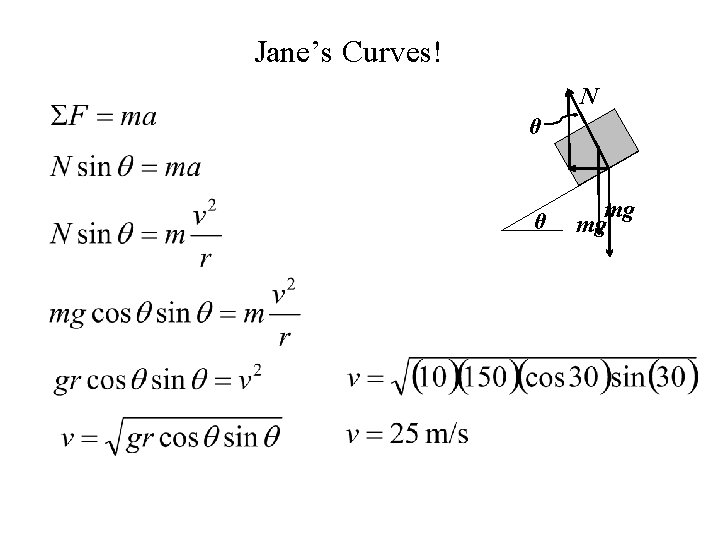
Jane’s Curves! • On the way to Nairobi one day to pick up a few supplies, Jane was driving around a banked curve of radius r = 150 m. Some naughty monkeys had thrown banana peels onto the road making it essentially frictionless. If the road was banked at an angle of θ = 30. °, what speed would she need to drive to maintain her position (not slip up or down)?

Jane’s Curves! N θ θ mg mg


Cheetah Dances! • On day, after he found Tarzan’s stash of home-brewed Serengeti Special, and drank a couple bottles, Cheetah put on quite the show. If he completes two revolutions (4π radians) per second, determine the velocity of the empty bottle in his hand. The bottle is located 0. 80 m from the center of his body, which is the axis of rotation.


Elephant Power! • Tarzan’s mother-in-law came for an extended visit and when she was finally ready to leave, her Jeep was stuck. Tarzan called an elephant friend named Shep to help out. If the powerful pachyderm was pushing with a force of 2500 N when he had the vehicle moving at 20. m/s, what was his power output?


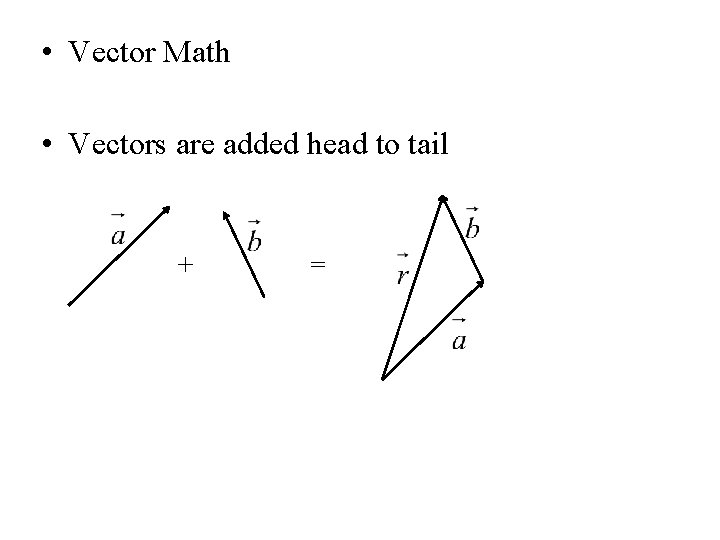
• Vector Math • Vectors are added head to tail + =

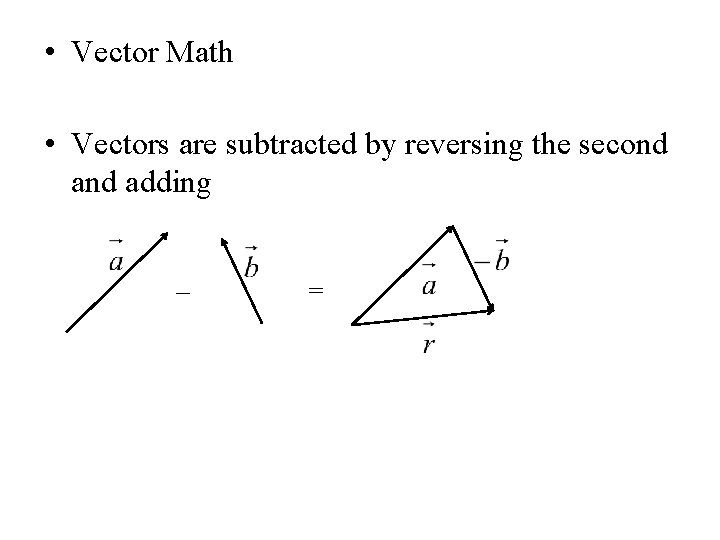
• Vector Math • Vectors are subtracted by reversing the second adding – =

• Vector Math • Vectors are multiplied two ways: 1) Dot product 2) Cross product

• Vector Math • Fundamentally, • A dot product is • A cross product is

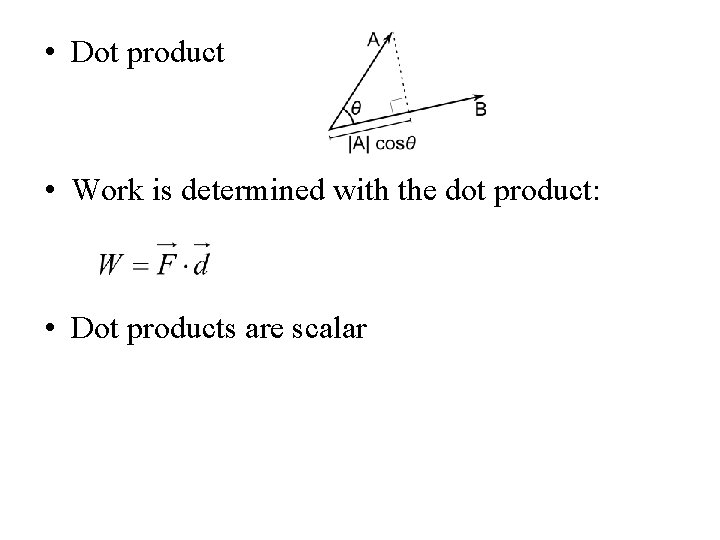
• Dot product • Work is determined with the dot product: • Dot products are scalar