Unit 2 Matriks A Determinan dan Invers matriks

Unit 2 Matriks A. Determinan dan Invers matriks B. Penyelesaian Sistem Persamaan Linear Matematika untuk kelas XI SMA Kelompok Peminatan

Diskusi Dalam kehidupan sehari-hari, banyak permasalahan yang melibatkan pengoptimalan, seperti meminimumkan ongkos atau memaksimalkan laba. Bersama teman sebangkumu, carilah satu permasalahan dalam kehidupan sehari-hari yang melibatkan pengoptimalan. Kemudian, selesaikan dengan menggunakan program linear, dan presentasikan hasilnya di depan kelas.

Bersyukurlah kepada Tuhan dengan adanya ilmu fisika dan matematika yang dapat dikolaborasikan untuk menyelesaikan suatu permasalahan

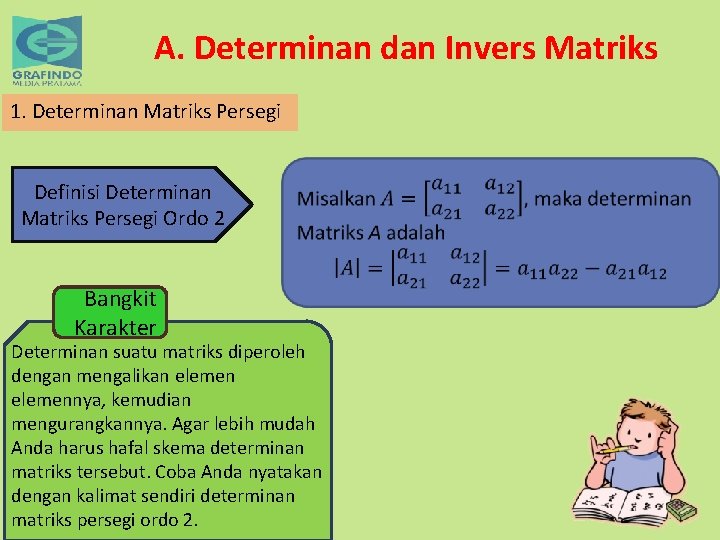
A. Determinan dan Invers Matriks 1. Determinan Matriks Persegi Definisi Determinan Matriks Persegi Ordo 2 Bangkit Karakter Determinan suatu matriks diperoleh dengan mengalikan elemennya, kemudian mengurangkannya. Agar lebih mudah Anda harus hafal skema determinan matriks tersebut. Coba Anda nyatakan dengan kalimat sendiri determinan matriks persegi ordo 2.

Contoh Soal •

Menghitung Determinan Matriks Persegi Ordo 3 dengan Metode Sarrus • Langkah 1. Salin dua kolom pertama dari determinan disebelah tanda pisah (Gambar 2. 1 Halaman 28).

Contoh Soal Tentukan determinan dari matriks . Penyelesaian: Langkah 1. Langkah 2 dan Langkah 3. Salin dua kolom pertama di sebelah Buat diagonal utama dan dua garis lain yang kanan tanda terpisah. sejajar diagonal utama. Buat juga diagonal sekunder dan 2 garis lain sejajar diagonal sekunder. Untuk Langkah 4 ada di Halaman 29.

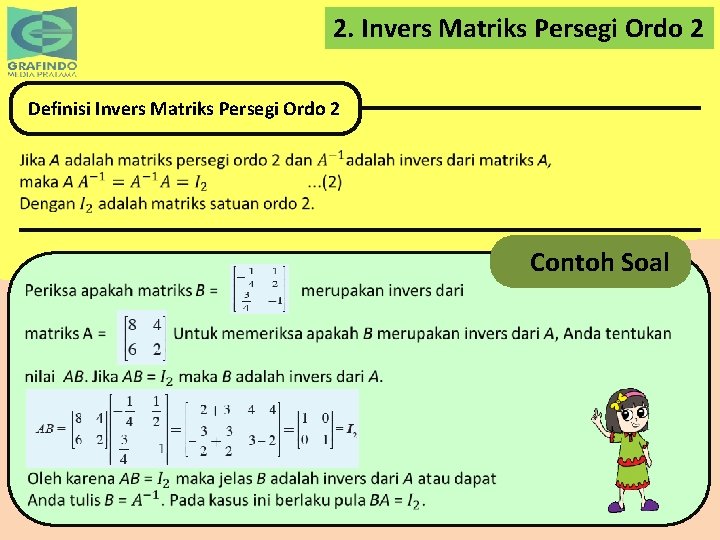
2. Invers Matriks Persegi Ordo 2 Definisi Invers Matriks Persegi Ordo 2 Contoh Soal

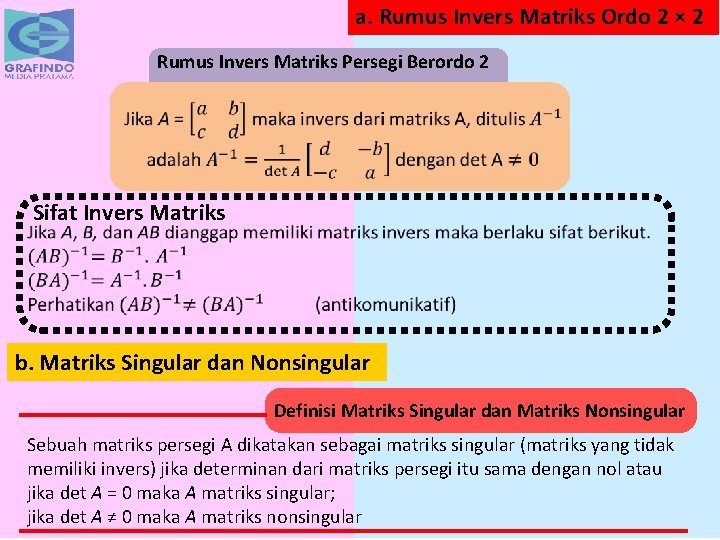
a. Rumus Invers Matriks Ordo 2 × 2 C. Nilai Stasioner Rumus Invers Matriks Persegi Berordo 2 Sifat Invers Matriks b. Matriks Singular dan Nonsingular Definisi Matriks Singular dan Matriks Nonsingular Sebuah matriks persegi A dikatakan sebagai matriks singular (matriks yang tidak memiliki invers) jika determinan dari matriks persegi itu sama dengan nol atau jika det A = 0 maka A matriks singular; jika det A ≠ 0 maka A matriks nonsingular

Contoh Soal Diketahui matriks A = Carilah bilangan x sehingga matriks A – x. I adalah matriks singular. Penyelesian: Syarat A – x. I singular adalah det[A – x. I] = 0, Jadi, nilai x yang memenuhi adalah x = 5 atau x = – 1.

Soal Latihan Kegiatan Kerjakan Uji Materi 2. 1 halaman 34, buku Matematika untuk Kelas XI SMA Kelompok Wajib.

B. Penyelesaian Sistem Persamaan Linear 1. Penyelesaian SPL Dua Variabel dengan Invers Matriks Contoh Soal Tentukan penyelesaian SPL berikut dengan matriks 2 x – y = 5 3 x + 2 y = 4

Langkah 1. Tidak perlu dilakukan karena SPL sudah dalam bentuk umum. Langkah 2. Ubah SPL ke bentuk persamaan matriks AX = B. Langkah 3. Tentukan matriks invers A– 1 dengan rumus invers matriks ord 2 × 2 Untuk Langkah 4 dan Langkah 5 ada pada Halaman 36

2. Aplikasi Penyelesaian SPL Dua Variabel dengan Invers Matriks Salah satu keuntungan besar menggunakan invers matriks dalam penyelesaian SPL adalah memudahkan Anda menyelesaikan SPL lain yang dibentuk hanya dengan mengubah tetapan-tetapan SPL (tidak mengubah koefisien-koefisien dari SPL). Contoh Soal Penyelesaian ada pada Halaman 37

3. Penyelesaian SPL dengan Determinan Penyelesaian SPL Dua Variabel dengan Determinan Materi tentang matriks dapat dilihat pada situs § http: //www. edhelper. co m/ Matrices. htm § http: //home. scarlet. be/~ping 1339/matr. htm Contoh Soal Penyelesaian: SPL telah disusun sesuai dengan bentuk umum yang diinginkan sehingga Anda dapat langsung menentukan determinan dari matriks koefisien, yaitu Jawaban selanjutnya ada pada Halaman 40 Tentukan penyelesaian

Langkah-Langkah Penyelesaian SPL Tiga Variabel dengan Metode Determinan 1. Misalkan, SPL tiga peubah dalam bentuk matriks adalah dengan A adalah matriks koefisien dari SPL dan B matriks tetapan dari SPL. 2. Tentukan determinan matriks A. 4. Penyelesaian SPL 3 Variabel dengan Determinan (*) 4. Bentuk matriks Y' dengan cara mengganti kolom 2 matriks A dengan matriks kolom B, kemudian tentukan determinan Y'. 5. Bentuk matriks Z' dengan cara mengganti kolom 3 matriks A dengan matriks kolom B, kemudian tentukan determinan Z'. 3. Bentuk matriks X' dengan cara mengganti kolom ke-1 matriks A 6. Jika D ≠ 0 maka penyelesaian SPL tiga dengan matriks kolom B (tetapan SPL), peubah adalah kemudian tentukan determinan X’.

Contoh Soal Selesaikan SPL berikut x + y + z = 5; 2 x – 4 y – 3 z = – 5; x – y = 4 Penyelesaian: Anda dapat menyatakan SPL tersebut ke dalam persamaan matriks berikut Tentukan determinan dari matriks koefisien adalah

Soal Latihan 1. Lena meminjam Rp 80. 000, 00 dalam tiga kategori pinjaman berbeda untuk memulai menjalankan bisnisnya. Ia meminjam dari dua bank sejumlah Rp 70. 000, 00 masing dengan bunga 11% dan 10%. Sisa lainnya dipinjam dari lembaga keuangan dengan bunga 13%. Berapa besar pinjaman Lena pada setiap kategori jika bunga tahunan yang harus dibayarnya adalah Rp 8. 500. 000, 00? 2. Jika matriks tidak mempunyai invers, tentukan nilai 2 y + 1. Kegiatan Kerjakan Uji Materi 2. 2 halaman 43 buku Matematika untuk Kelas XI SMA Kelompok Wajib.

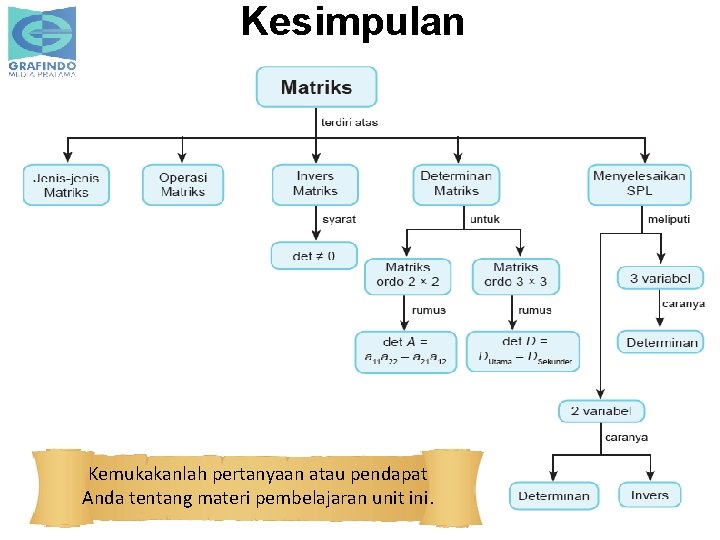
Kesimpulan Kemukakanlah pertanyaan atau pendapat Anda tentang materi pembelajaran unit ini.

Kuis Kegiatan Kerjakan Uji Kompetensi Unit 2 halaman 44 buku Matematika untuk Kelas XI SMA Kelompok Wajib.

Terima Kasih Rahasia sukses dalam hidup itu adalah menemukan suatu takdirnya dan kemudian melakukannya. -Henry Ford-.

referensi • www. photo. dhakasite. com • www. smamarsudirinimtl. c om

Created by: Fitriana Suci Rahayu