Unit 2 Fundamentals of Statistics Definitions of Statistics

Unit 2 Fundamentals of Statistics

Definitions of Statistics • A collection of quantitative data. . • Science of systematic gathering and analysis. . . of data. . .

Collection of Data • Variables (measurable quality characteristics): – Lengths – Voltage – Resistance • Attributes (conforming or nonconforming quality characteristics): – go/no go gage – Visual inspection of painted products

Some Measurements in quality Dimensional Temperatures Voltage Resistance Hardness Speed Weight Height Volume Sound Numbers Brightness Roundness Roughness Thickness Ages Rate Angles Time Distance Humidity

Some Attributes in quality • • Finish Smoothness Go/No-Go Inspection Yes-No Inspection

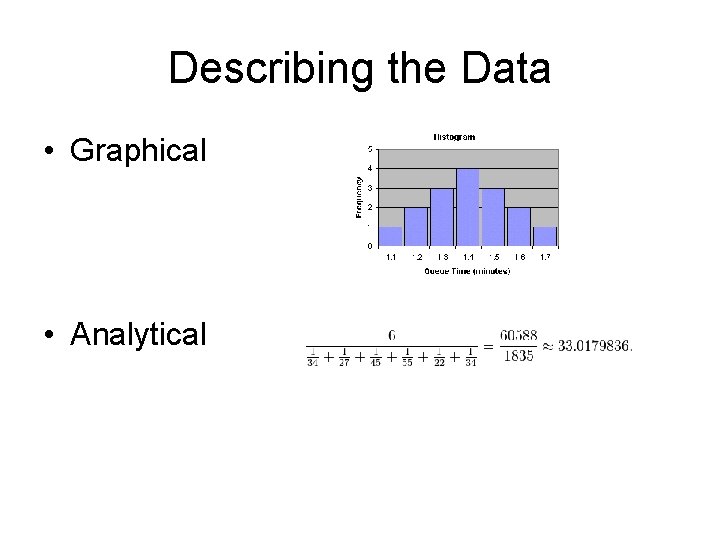
Describing the Data • Graphical • Analytical

Frequency Distribution • • Ungrouped data Grouped data Tally sheet Histograms

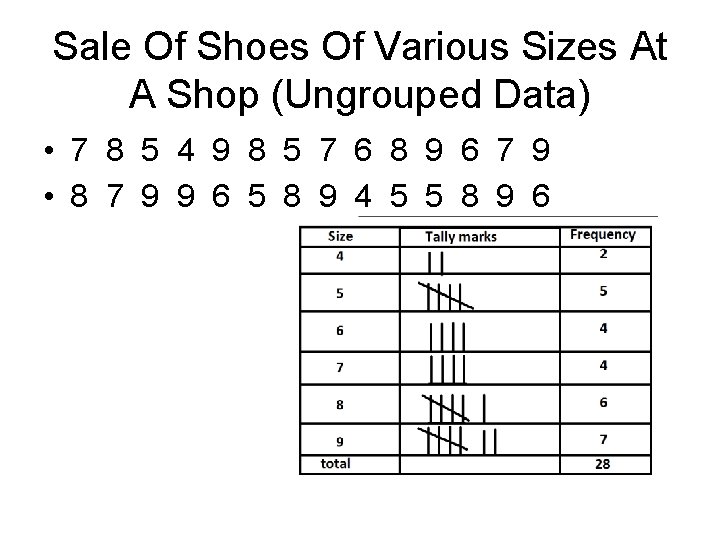
Sale Of Shoes Of Various Sizes At A Shop (Ungrouped Data) • 7 8 5 4 9 8 5 7 6 8 9 6 7 9 • 8 7 9 9 6 5 8 9 4 5 5 8 9 6

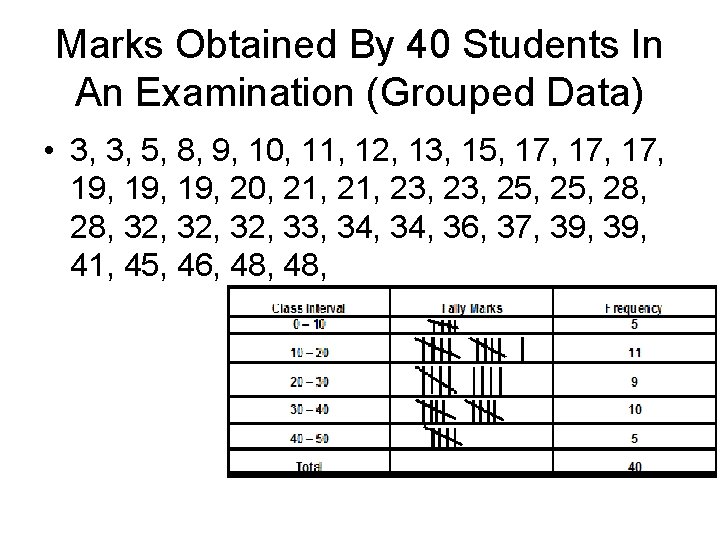
Marks Obtained By 40 Students In An Examination (Grouped Data) • 3, 3, 5, 8, 9, 10, 11, 12, 13, 15, 17, 17, 19, 19, 20, 21, 23, 25, 28, 32, 32, 33, 34, 36, 37, 39, 41, 45, 46, 48,

Tally Sheet Sample (Excel) 2. 002 IIIII 9 2. 021 IIIII II 2. 043 IIIII II 2. 048 IIIII III 13 2. 051 IIIII II 12 2. 057 IIIII 10 2. 064 IIIII II 12 7 7

Steps In Preparing And Presenting Grouped Data • Collect data and prepare a tally sheet – – • Determine the range – – • R = Xh – Xl (R = range; Xh = Highest number; Xl = Lowest number) Determine the cell interval – • i = R/(1 + 3. 322 log n) Determine the cell mid point – • • Data sheet Tally sheet MPl = Xl + i/2 Determine the cell boundaries Post the cell frequency

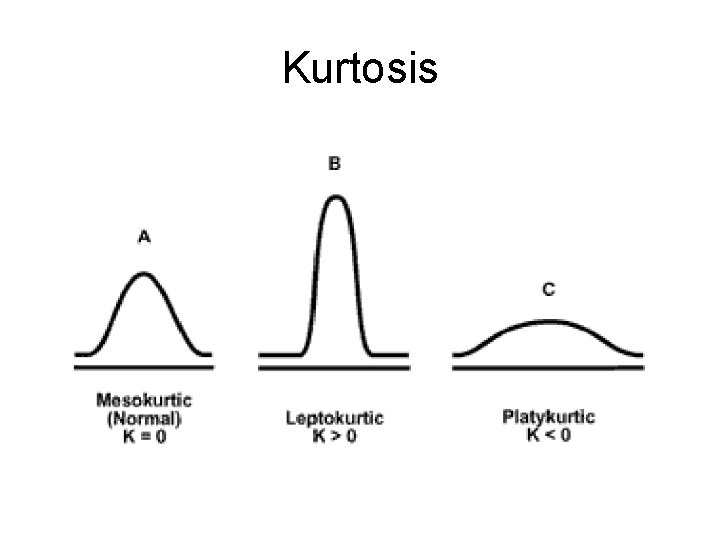
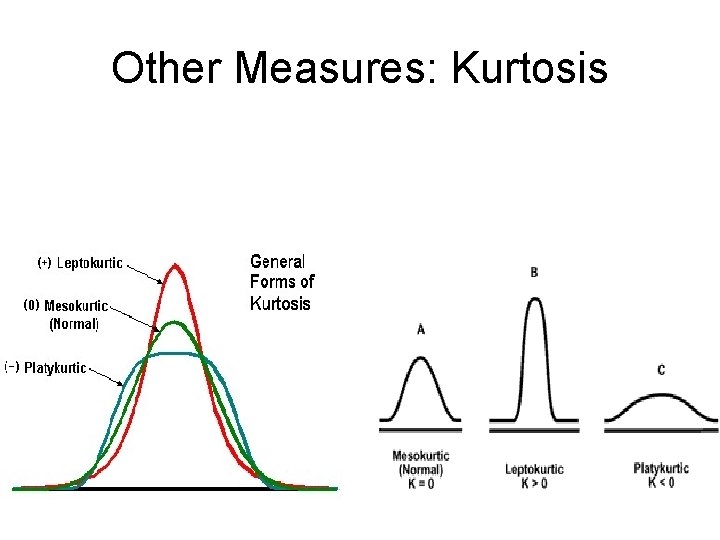
Characteristics of Frequency Distribution Graphs • • Population frequency distribution Sample frequency distribution Analysis of histograms Symmetry Modal characteristics Leptokurtic Platycurtic

Kurtosis

Measures of Central Tendency • Average: 1, 3, 3, 5, 5, 5, 6, 7, 7, 8, 11 • Median: 1, 3, 3, 5, 5, 5, 6, 7, 7, 8, 11 • Mode: 1, 3, 3, 5, 5, 5, 6, 7, 7, 8, 11

Relationship Among the Measures of Central Tendency • All are identical when there is symmetrical distribution • Average is the most commonly used measure of central tendency • Median is effective when distribution is skewed • Mode is use to determine the most likely value of a distribution

Relationship Among the Measures of Dispersion • The range is very simple to calculate, and ideal when the amount of data is too small or too scattered • The accuracy of the range decreases as the number of observations increases • The standard deviation is ideal for more precise measure of variation • As the standard deviation gets smaller, the quality gets better

Computing Standard Deviation μ = σ =

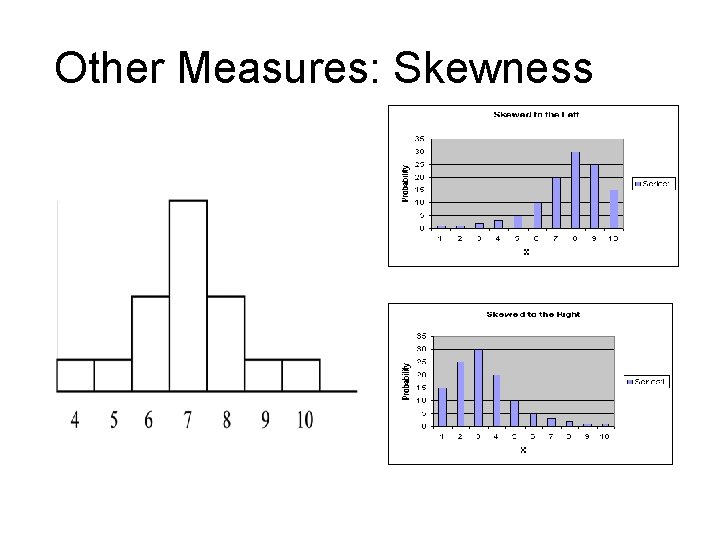
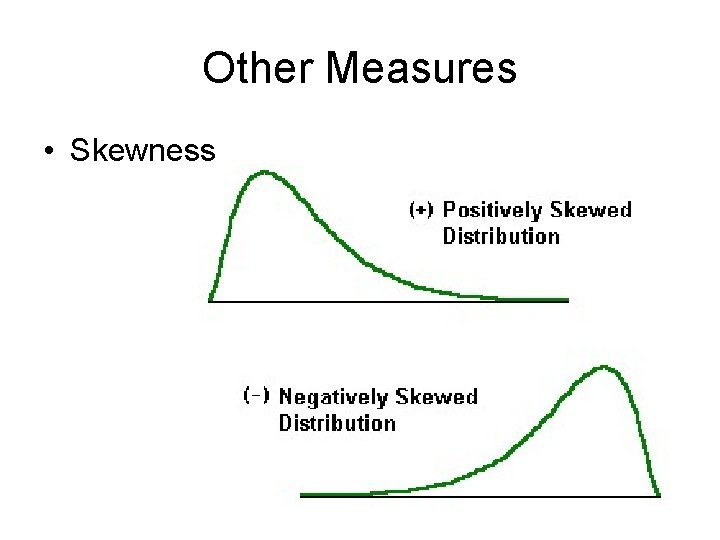
Other Measures: Skewness

Other Measures • Skewness

Other Measures: Kurtosis

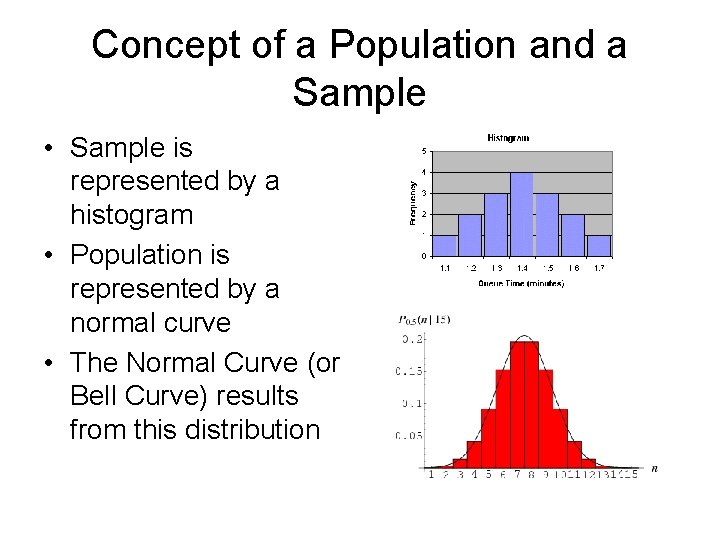
Concept of a Population and a Sample Sampling is that part of statistical practice concerned with the selection of a subset of individual observations within a population of individuals intended to yield some knowledge about the population of concern, especially for the purposes of making predictions based on statistical inference.

Concept of a Population and a Sample • The selected members are called the Sample • The group from which the sample was selected is called the Population

Concept of a Population and a Sample • Sample is represented by a histogram • Population is represented by a normal curve • The Normal Curve (or Bell Curve) results from this distribution

The Normal Curve (or Bell Curve) Principle • Is a graph representing the density function of the normal probability distribution • Also referred to as the Normal Curve or Bell Curve • To draw a normal curve, one needs to specify the mean and the standard deviation • The curve is made up of 6 standard deviations • A Normal distribution with a mean of zero and a standard deviation of 1 is known as the Standard Normal Distribution

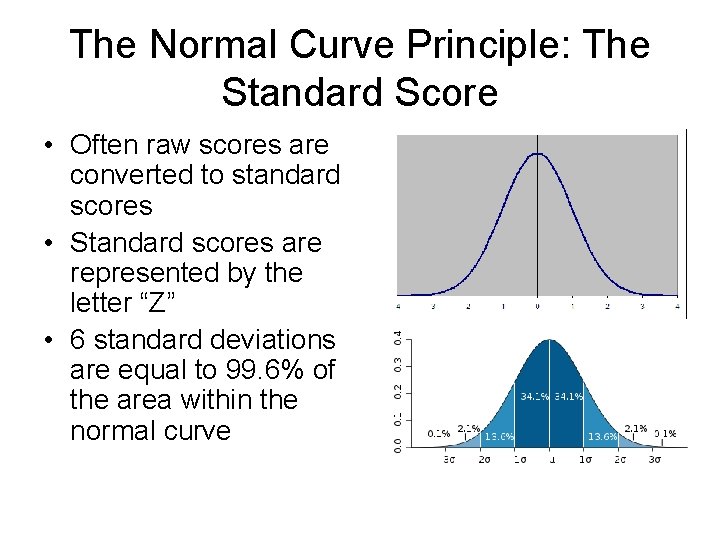
The Normal Curve Principle: The Standard Score • Often raw scores are converted to standard scores • Standard scores are represented by the letter “Z” • 6 standard deviations are equal to 99. 6% of the area within the normal curve

Standardized normal value “z” or Standard Score • The standard score is Ø • where: Øx is a raw score to be standardized; Øμ is the mean of the population; Øσ is the standard deviation of the population

Applications of the Normal curve Principles • • In quality control In statistics In business management In every discipline known to man