UNIT 2 5 GRAPHS OF EXPENSE AND REVENUE

UNIT 2. 5 GRAPHS OF EXPENSE AND REVENUE FUNCTIONS Monday 10/16/17

Slide 2 Key Terms • • nonlinear function second-degree equation quadratic equation parabola • • leading coefficient maximum value vertex of a parabola axis of symmetry

Slide 3 HOW CAN EXPENSE AND REVENUE BE GRAPHED? Non-Linear Functions, when graphed, that are NOT a straight line

Slide 4 HOW CAN EXPENSE AND REVENUE BE GRAPHED? 2 nd Degree Equation Quadratic Equation An equation that has a variable raised to the 2 nd degree. Usually a quadratic equation One which takes the form … ax 2 + bx + c if a≠ 0

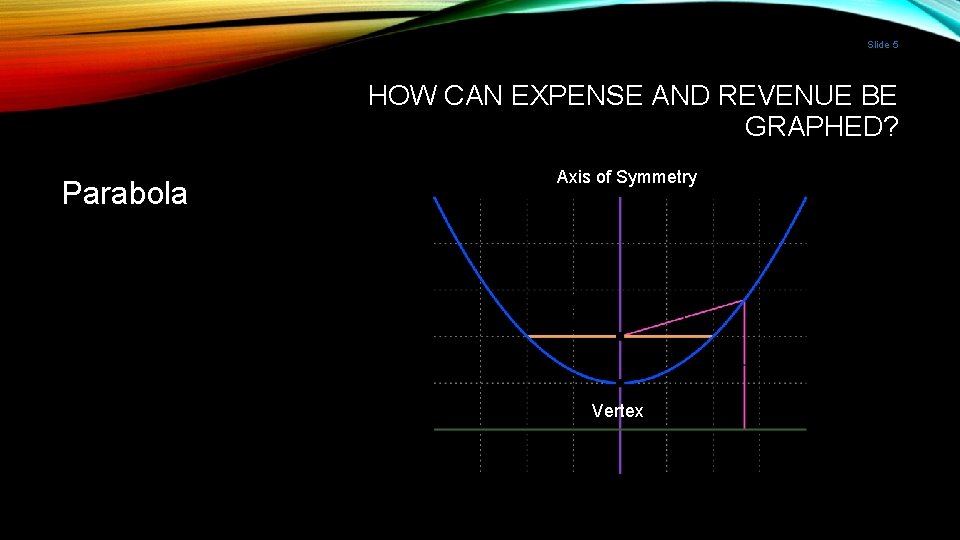
Slide 5 HOW CAN EXPENSE AND REVENUE BE GRAPHED? Parabola Axis of Symmetry Vertex

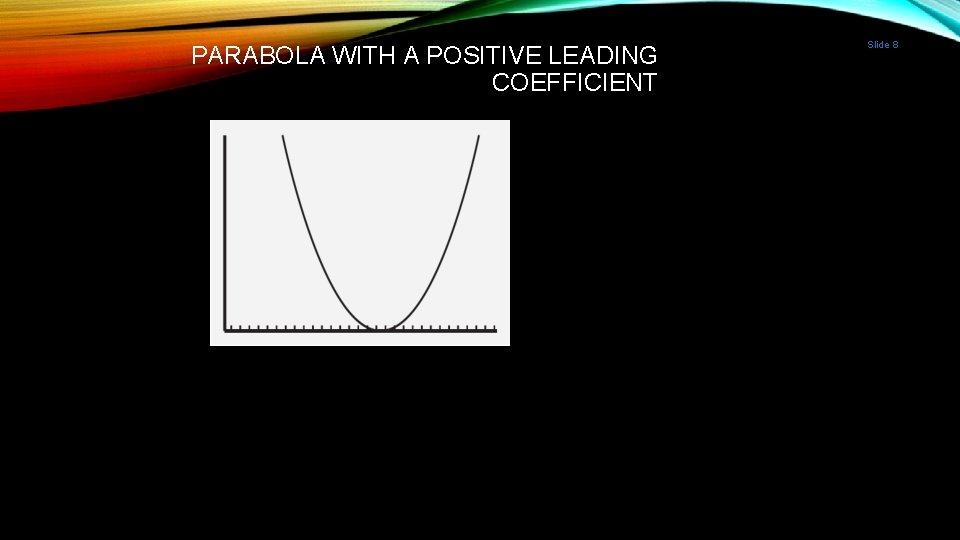
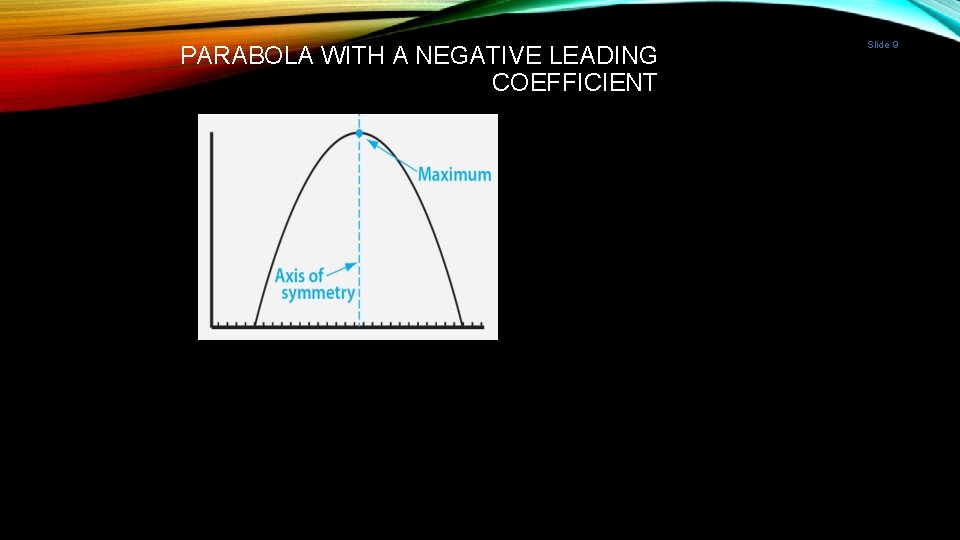
Slide 6 HOW CAN EXPENSE AND REVENUE BE GRAPHED? Leading Coefficient The “a” in the quadratic equation ax 2 + bx + c If a>0 then parabola opens up If a<0 then parabola opens down

Slide 7 HOW CAN EXPENSE AND REVENUE BE GRAPHED? Vertex Axis of Symmetry The “top” of a parabola that opens down or the “bottom” of a parabola that opens up Vertical line drawn through vertex that dissects the parabola equally x = b/-2 a

PARABOLA WITH A POSITIVE LEADING COEFFICIENT Slide 8

PARABOLA WITH A NEGATIVE LEADING COEFFICIENT Slide 9

EXAMPLE 1 A particular item in the Picasso Paints product line costs $7. 00 each to manufacture. The fixed costs are $28, 000. The demand function is q = – 500 p + 30, 000 where q is the quantity the public will buy given the price, p. Graph the expense function in terms of price on the coordinate plane. Slide 10

CHECK YOUR UNDERSTANDING An electronics company manufactures earphones for portable music devices. Each earphone costs $5 to manufacture. Fixed costs are $20, 000. The demand function is q = – 200 p + 40, 000. Write the expense function in terms of q and determine a suitable viewing window for that function. Graph the expense function. Slide 11

EXAMPLE 2 What is the revenue equation for the Picasso Paints product? Write the revenue equation in terms of the price. Slide 12

CHECK YOUR UNDERSTANDING Determine the revenue if the price per item is set at $25. 00. Slide 13

EXAMPLE 3 Graph the revenue equation on a coordinate plane. Slide 14

CHECK YOUR UNDERSTANDING Use the graph in Example 3. Which price would yield the higher revenue, $28 or $40? Slide 15

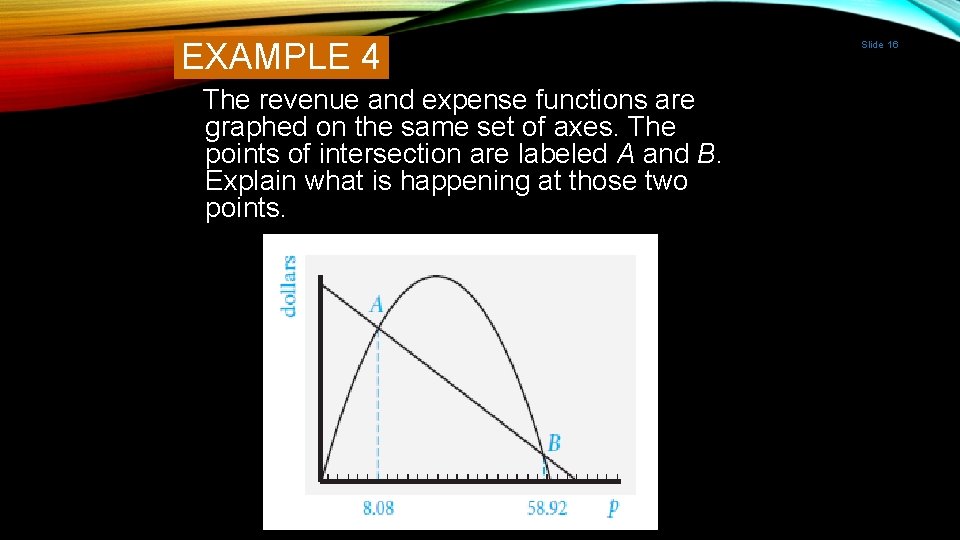
EXAMPLE 4 The revenue and expense functions are graphed on the same set of axes. The points of intersection are labeled A and B. Explain what is happening at those two points. Slide 16

CHECK YOUR UNDERSTANDING Why is using the prices of $7. 50 and $61. 00 not in the best interest of the company? Slide 17