Unit 18 Vibrationdata Digital Filtering plus some seismology

Unit 18 Vibrationdata Digital Filtering (plus some seismology) 1

Introduction Vibrationdata n Filtering is a tool for resolving signals n Filtering can be performed on either analog or digital signals n Filtering can be used for a number of purposes n n n For example, analog signals are typically routed through a lowpass filter prior to analog-to-digital conversion The lowpass filter in this case is designed to prevent an aliasing error This is an error whereby high frequency spectral components are added to lower frequencies 2

Introduction (Continued) n Vibrationdata Another purpose of filtering is to clarify resonant behavior by attenuating the energy at frequencies away from the resonance n This Unit is concerned with practical application and examples n It covers filtering in the time domain using a digital Butterworth filter n This filter is implemented using a digital recursive equation in the time domain 3

Highpass & Lowpass Filters n n n Vibrationdata A highpass filter is a filter which allows the high-frequency energy to pass through It is thus used to remove low-frequency energy from a signal A lowpass filter is a filter which allows the low-frequency energy to pass through It is thus used to remove high-frequency energy from a signal A bandpass filter may be constructed by using a highpass filter and lowpass filter in series 4

Butterworth Filter Characteristics n Vibrationdata A Butterworth filter is one of several common infinite impulse response (IIR) filters n Other filters in this group include Bessel and Chebyshev filters n These filters are classified as feedback filters n n n The Butterworth filter can be used either for highpass, lowpass, or bandpass filtering A Butterworth filter is characterized by its cut-off frequency The cut-off frequency is the frequency at which the corresponding transfer function magnitude is – 3 d. B, equivalent to 0. 707 5

Butterworth Filter (Continued) Vibrationdata n A Butterworth filter is also characterized by its order n A sixth-order Butterworth filter is the filter of choice for this Unit n n A property of Butterworth filters is that the transfer magnitude is – 3 d. B at the cut-off frequency regardless of the order Other filter types, such as Bessel, do not share this characteristic Consider a lowpass, sixth-order Butterworth filter with a cut-off frequency of 100 Hz The corresponding transfer function magnitude is given in the following figure 6
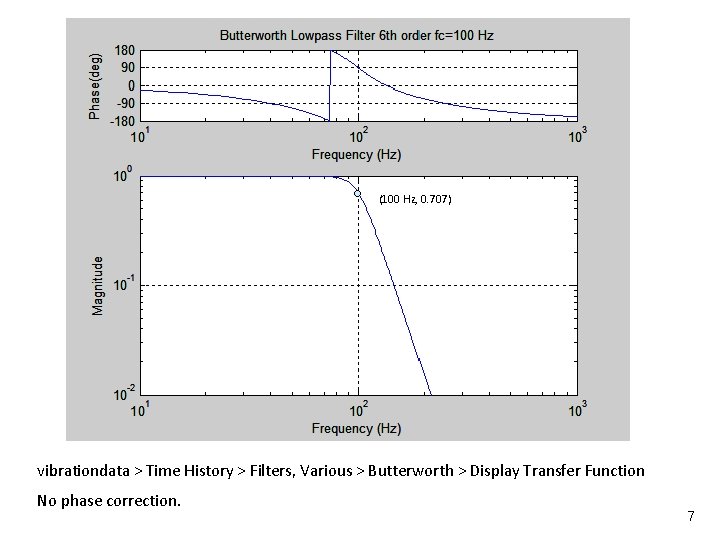
Vibrationdata (100 Hz, 0. 707) vibrationdata > Time History > Filters, Various > Butterworth > Display Transfer Function No phase correction. 7

Transfer Function Characteristics n n Vibrationdata Note that the curve in the previous figure has a gradual roll-off beginning at about 70 Hz Ideally, the transfer function would have a rectangular shape, with a corner at (100 Hz, 1. 00 ) n This ideal is never realized in practice n Thus, a compromise is usually required to select the cut-off frequency n n The transfer function could also be represented in terms of a complex function, with real and imaginary components A transfer function magnitude plot for a sixth-order Butterworth filter with a cut-off frequency of 100 Hz as shown in the next figure 8
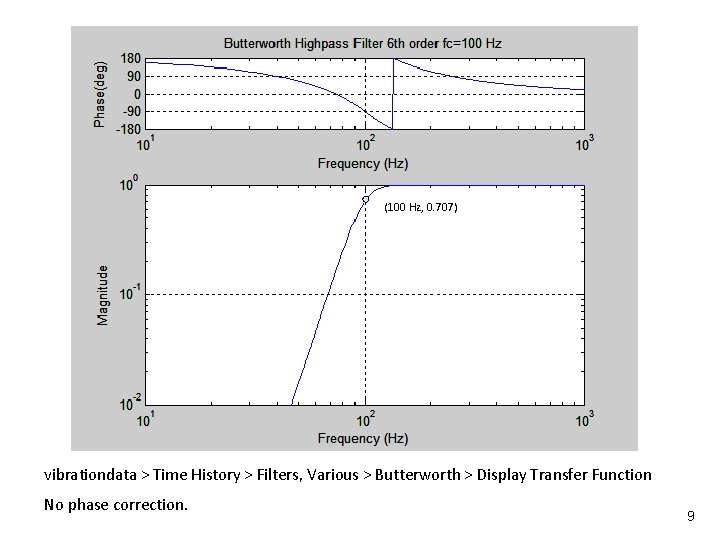
Vibrationdata (100 Hz, 0. 707) vibrationdata > Time History > Filters, Various > Butterworth > Display Transfer Function No phase correction. 9
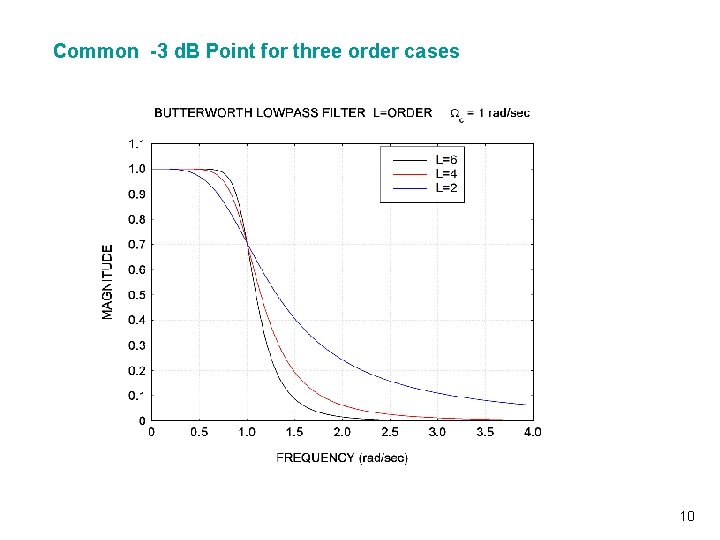
Common -3 d. B Point for three order cases Vibrationdata 10

Frequency Domain Implementation n Vibrationdata The curves in the previous figures suggests that filtering could be achieved as follows: 1. Take the Fourier transform of the input time history 2. Multiply the Fourier transform by the filter transfer function, in complex form 3. Take the inverse Fourier transform of the product n n The above frequency domain method is valid Nevertheless, the filtering algorithm is usually implemented in the time domain for computational efficiency, to avoid leakage error, etc. 11
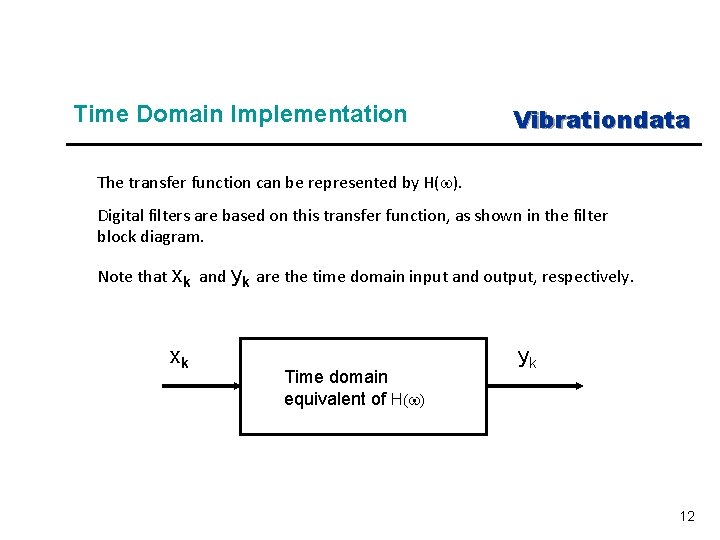
Time Domain Implementation Vibrationdata The transfer function can be represented by H(w). Digital filters are based on this transfer function, as shown in the filter block diagram. Note that xk and yk are the time domain input and output, respectively. xk Time domain equivalent of H(w) yk 12

Time Domain Implementation Vibrationdata The filtering equation is implemented as a digital recursive filtering yk relationship. The response is where xk is the input an & bn are coefficients L is the order 13

Phase Correction Vibrationdata n Ideally, a filter should provide linear phase response n This is particularly desirable if shock response spectra calculations are required n Butterworth filters, however, do not have a linear phase response n Other IIR filters share this problem n A number of methods are available, however, to correct the phase response n One method is based on time reversals and multiple filtering as shown in the next slide 14
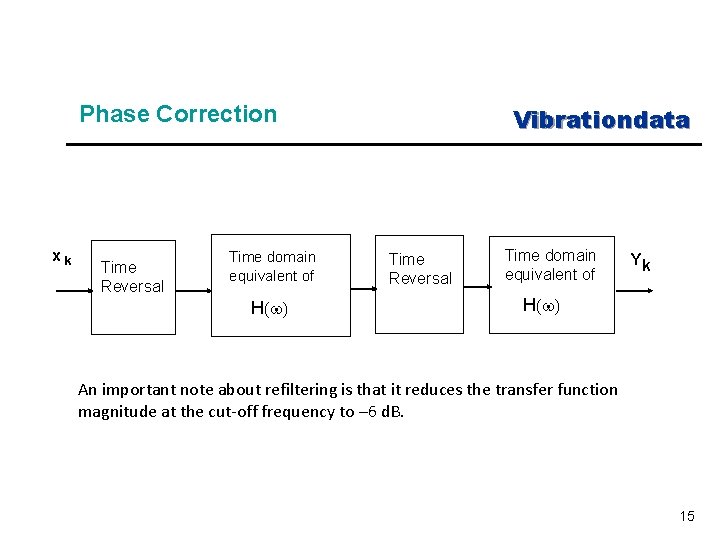
Phase Correction xk Time Reversal Time domain equivalent of H(w) Vibrationdata Time Reversal Time domain equivalent of Yk H(w) An important note about refiltering is that it reduces the transfer function magnitude at the cut-off frequency to – 6 d. B. 15
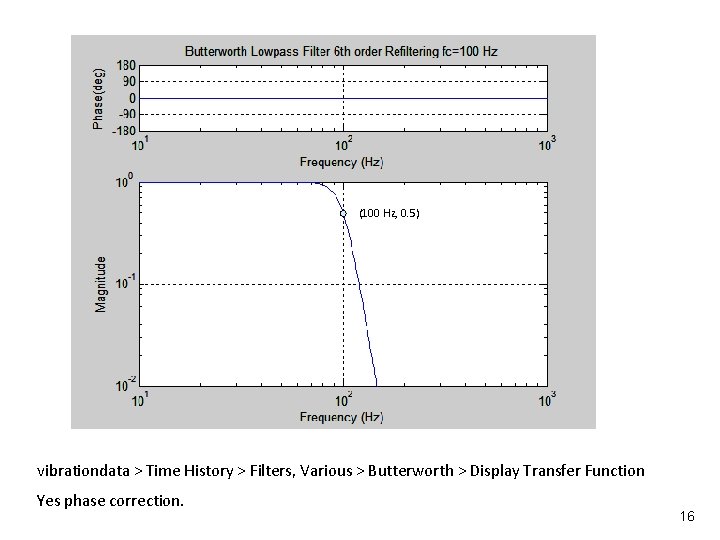
Vibrationdata (100 Hz, 0. 5) vibrationdata > Time History > Filters, Various > Butterworth > Display Transfer Function Yes phase correction. 16

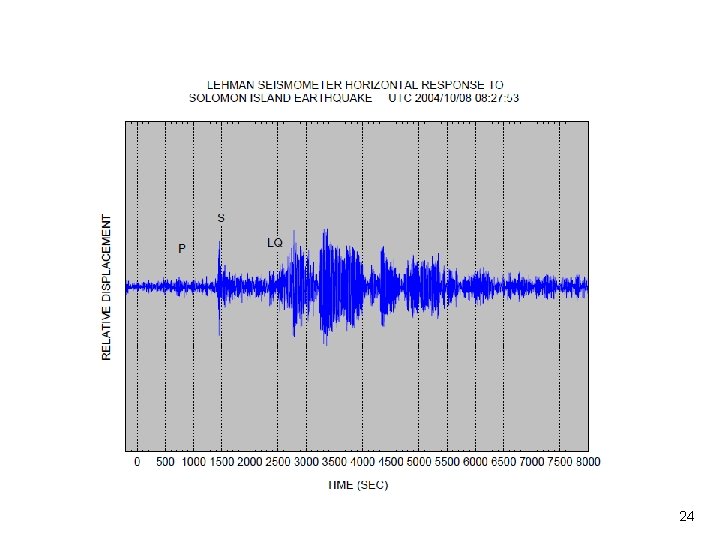
Filtering Example Vibrationdata • Use filtering to find onset of P-wave in seismic time history from Solomon Island earthquake, October 8, 2004 • Magnitude 6. 8 • Measured data is from homemade seismometer in Mesa, Arizona 17

Homemade Lehman Seismometer Vibrationdata 18

Non-contact Vibrationdata Displacement Transducer 19

Ballast Mass Partially Submerged in Oil Vibrationdata 20

Pivot End of the Boom Vibrationdata 21
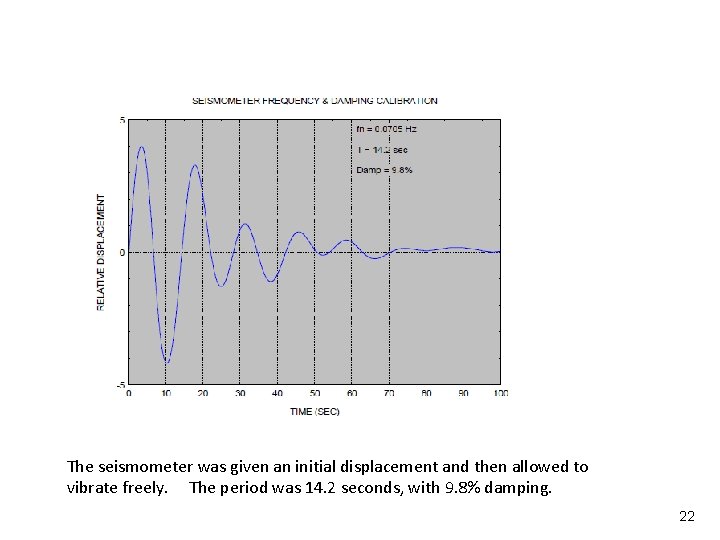
Vibrationdata The seismometer was given an initial displacement and then allowed to vibrate freely. The period was 14. 2 seconds, with 9. 8% damping. 22

Vibrationdata 23
Vibrationdata 24
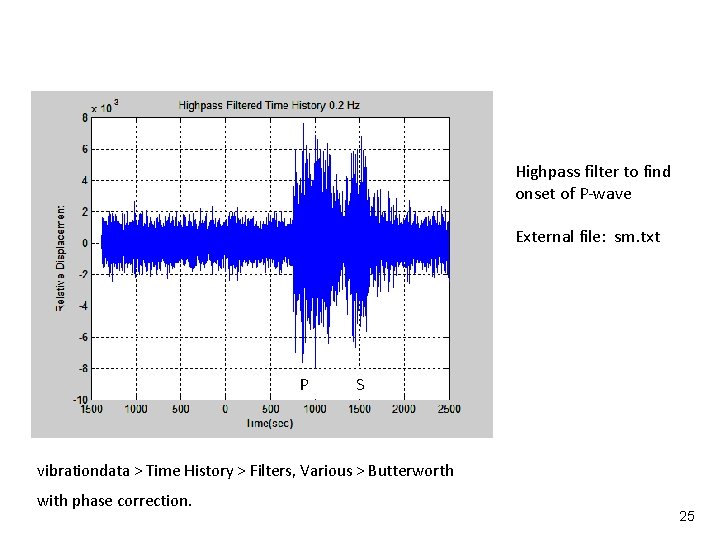
Vibrationdata Highpass filter to find onset of P-wave External file: sm. txt P S vibrationdata > Time History > Filters, Various > Butterworth with phase correction. 25

Characteristic Seismic Wave Periods Vibrationdata Wave Type Period (sec) Natural Frequency (Hz) Body 0. 01 to 50 0. 02 to 100 Surface 10 to 350 0. 003 to 0. 1 Reference: Lay and Wallace, Modern Global Seismology 26
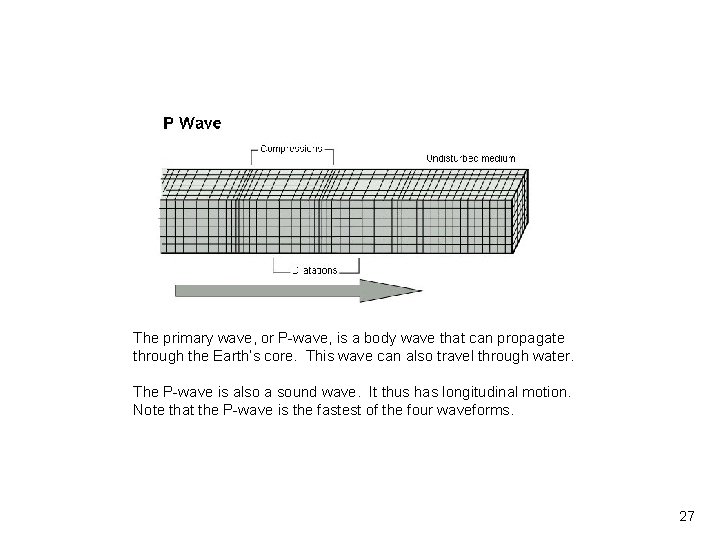
Vibrationdata The primary wave, or P-wave, is a body wave that can propagate through the Earth’s core. This wave can also travel through water. The P-wave is also a sound wave. It thus has longitudinal motion. Note that the P-wave is the fastest of the four waveforms. 27
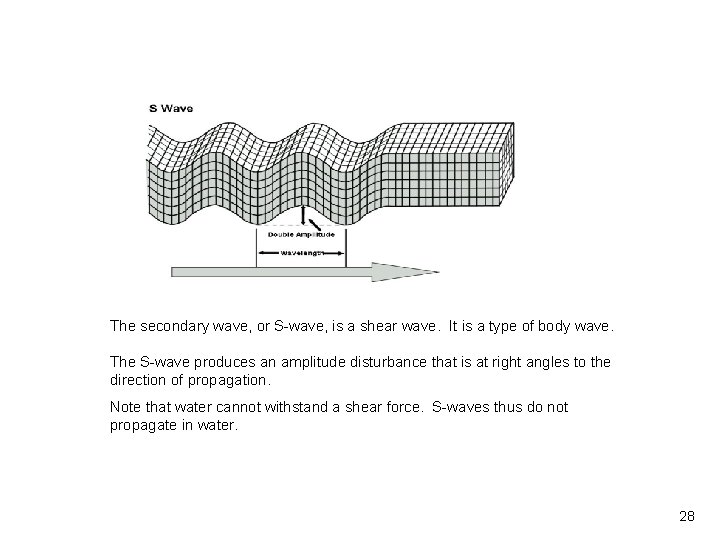
Vibrationdata The secondary wave, or S-wave, is a shear wave. It is a type of body wave. The S-wave produces an amplitude disturbance that is at right angles to the direction of propagation. Note that water cannot withstand a shear force. S-waves thus do not propagate in water. 28
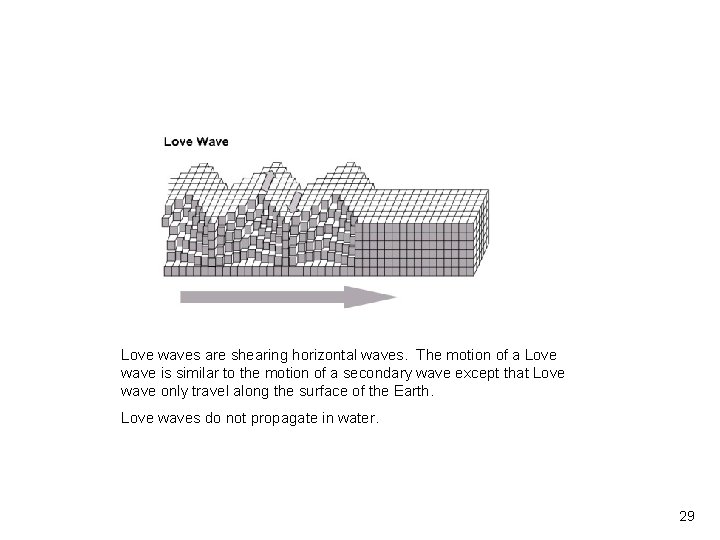
Vibrationdata Love waves are shearing horizontal waves. The motion of a Love wave is similar to the motion of a secondary wave except that Love wave only travel along the surface of the Earth. Love waves do not propagate in water. 29

Vibrationdata Rayleigh waves travel along the surface of the Earth. Rayleigh waves produce retrograde elliptical motion. The ground motion is thus both horizontal and vertical. The motion of Rayleigh waves is similar to the motion of ocean waves except that ocean waves are prograde. 30
- Slides: 30