Unit 13 Gas Laws Gases in Real Life

Unit 13: Gas Laws

Gases in Real Life

Properties of Gases • Highest energy of all states of matter • There is a lot of “free” space in a gas • Gases can be expanded infinitely • Gases fill containers uniformly and completely • Gases diffuse and mix rapidly

Gas Law Variables •

Kinetic Molecular Theory= a theory that describes the behavior of gas particles (5 parts to theory) 1. Gases consist of tiny particles (atoms or molecules) 2. These particles are so small, compared with the distances between them, that the volume (size) of the individual particles can be assumed to be negligible (zero) 3. These particles are in constant random motion, colliding with the walls of the container. These collisions with the walls cause the pressure exerted by the gas. 4. The particles are assumed to not attract or repel each other. 5. The average kinetic energy of the gas particles is directly proportional to the Kelvin temperature of the gas.

Diffusion and Effusion • Diffusion is the gradual mixing of molecules of different gases. • Think about a person wearing perfume walking into a room • The person closest to the perfume smells it the most and the person furthest away smells it the least • The perfume is slowing diffusing and mixing with the air in the room • Effusion is the movement of molecules through a small hole. • Think about a tire with a small hole. What happens to the air in the tire? • It slowly effuses out • Effusion is usually followed by diffusion

Graham’s Law of Effusion/Diffusion • Graham’s Law relates rate or speed of diffusion of gases and their molar mass under the same conditions • Rate α 1/M • Heavier gases diffuse more slowly than lighter gases

Graham’s Law of Effusion/Diffusion • Example 1: A bottle of ammonia and a bottle of vinegar (acetic acid) are both opened at the same time equal distance away from you. Each bottle contains a small amount of gas that escapes when opened. Which gas, ammonia or acetic acid, would you smell first and why? • The ammonia because it has a smaller molar mass so it travels faster • Example 2: A balloon containing equal moles of helium gas and oxygen gas had a small leak and gas began to slowly effuse out of the balloon. After allowing the gas to escape for 30 seconds, the hole is sealed. Which of the remaining gases, helium or oxygen gas, will be in higher concentration inside the balloon and why? • The oxygen gas; the helium gas moves faster because it has a smaller molar mass, so more helium escaped than oxygen

STP • STP stands for Standard Temperature and Pressure • Gases behavior change when temperature and pressure are changed • For this reason we have a standard temperature and pressure • STP allows us to compare gases • Standard Temperature= 273 K • Standard Pressure= 1 atmosphere • At STP 1 mole of gas occupies 22. 4 L of space

Temperature • Temperature is a measure of average kinetic energy • Temperature can be measured in ◦F , ◦C , or K • Every problem this unit needs to be in units of K • K= ◦C + 273 • Matter cannot be cooled to temperature lower than -273 ◦C , therefore this temperature is called absolute zero -273 ◦C = 0 K • Temperature at STP is 273 K

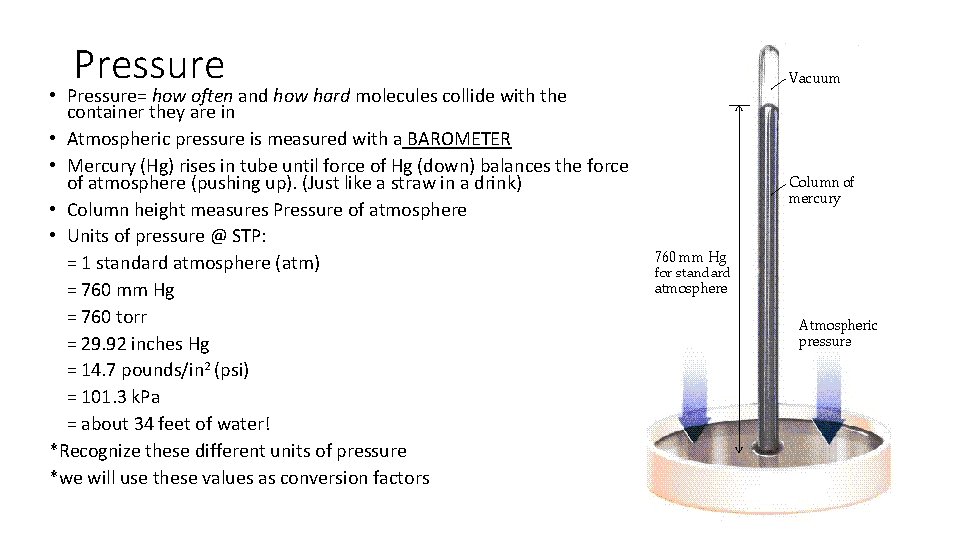
Pressure • Pressure= how often and how hard molecules collide with the container they are in • Atmospheric pressure is measured with a BAROMETER • Mercury (Hg) rises in tube until force of Hg (down) balances the force of atmosphere (pushing up). (Just like a straw in a drink) • Column height measures Pressure of atmosphere • Units of pressure @ STP: = 1 standard atmosphere (atm) = 760 mm Hg = 760 torr = 29. 92 inches Hg = 14. 7 pounds/in 2 (psi) = 101. 3 k. Pa = about 34 feet of water! *Recognize these different units of pressure *we will use these values as conversion factors

Pressure Conversions A. What is 475 mm Hg expressed in atm? 475 mm Hg 1 atm = 0. 625 atm 760 mm Hg B. The pressure of a tire is measured as 29. 4 psi. What is this pressure in mm Hg? 29. 4 psi 760 mm Hg 14. 7 psi = 1520 mm Hg

Pressure Conversions C. What is 2 atm expressed in torr? D. The pressure of a tire is measured as 32. 0 psi. What is this pressure in k. Pa?

Gases in the Air The % of Gases in Air Partial Pressure at STP 78. 08% N 2 593. 4 mm Hg 20. 95% O 2 159. 2 mm Hg 0. 94% Ar 7. 1 mm Hg 0. 03% CO 2 0. 2 mm Hg • The total pressure in the air is equal to the sum of all of the partial pressures caused by each gas in air • PAir = PN 2 + PO 2 + PAr + PCO 2 • PAir = 593. 4 mm Hg + 159. 2 mm Hg + 7. 1 mm Hg + 0. 2 mm Hg • PAir = 759. 9 mm Hg

Dalton’s Law of Partial Pressures • Dalton’s Law of Partial Pressures: The total pressure in a container is equal to the sum of the partial pressures of each gas within the container • Ptotal = PA + PB + PC + PD + … Example 1: What is the total pressure in a flask after all of the hydrogen peroxide has decomposed given the following information? 2 H 2 O 2 (l) ---> 2 H 2 O (g) + O 2 (g) 0. 32 atm 0. 16 atm Ptotal = PH 2 O + PO 2 = 0. 48 atm

Dalton’s Partial Pressure Practice Example 2: Oxygen and chlorine gas are mixed in a container with partial pressures of 401 mm. Hg and 0. 639 atm, respectively. What is the total pressure inside the container (in atm)? 1. 17 atm Example 3: Container A contains a gas under 3. 24 atm of pressure. Container B contains a gas under 2. 82 atm of pressure. Container C contains a gas under 1. 21 atm of pressure. If all of these gases are put into Container D, what is the pressure in Container D? 7. 27 atm

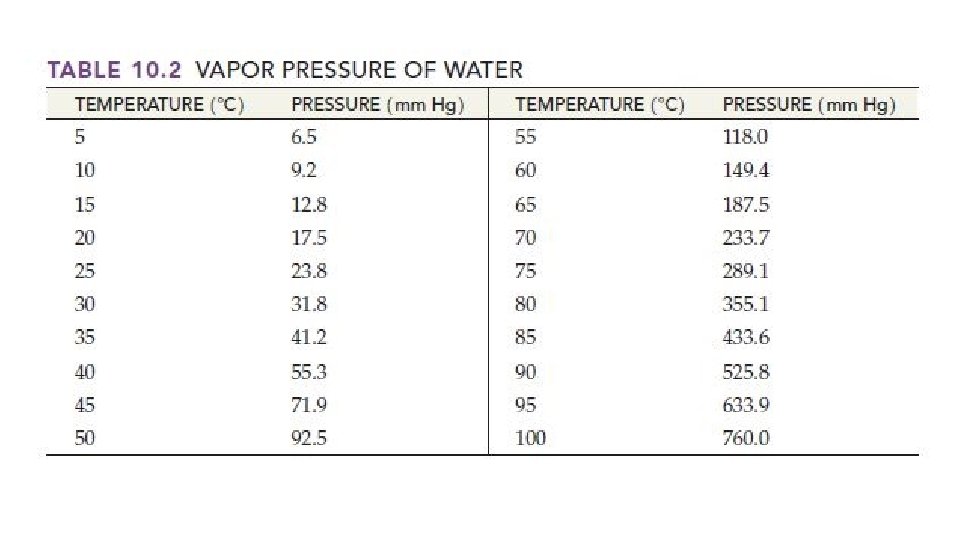
Collecting a Gas Over Water • Since gases mix with other gases, they must be collected in a pure environment. • The easiest way to do this is to collect a gas is collected “over water” • That means the reaction happens in a sealed container that allows the gas that is produced to flow through water and be collected in a container. • Collecting the gas over water allows you to collected a more pure sample than collecting it in air • The sample collected over water is not completely pure because there is water vapor present in the gas sample that is collected • The pressure inside the container is from the gas AND the water vapor. This is where Dalton’s Law of Partial Pressures becomes useful. • Pgas = Ptotal - Pwater • The total pressure inside the container is the same as the atmospheric pressure

Collecting a Gas Over Water Practice 1. A reaction produced an amount of helium gas at 85 degrees Celsius. The total pressure of the collected sample is 790 torr, what is the partial pressure of the helium gas? 2. A student collects some hydrogen gas over water at 20 degrees C and 768 torr. What is the pressure of the H 2 gas?

Avogadro's Hypothesis •

Avogadro’s Hypothesis Practice •

Boyle’s Law • P α 1/V • This means Pressure and Volume are INVERSELY PROPORTIONAL if moles and temperature are constant (do not change). For example, P goes up as V goes down. WHY? P 1 V 1 = P 2 V 2 • When discussing a change in volume the container must be flexible container that allows a change in volume *n and T are held constant Robert Boyle (1627 -1691). Son of Earl of Cork, Ireland.

Boyle’s Law Practice 1. A sample of oxygen gas occupies a volume of 250 m. L at 740 torr pressure. What volume will it occupy at 810 torr? V 1= 250 m. L P 1 V 1 = P 2 V 2 P 1= 740 torr (740)(250)=(810) V 2= ? P 2= 810 torr V = 230 m. L 2

Charles’s Law • Jacques Charles (17461823). Isolated boron and studied gases. Balloonist.

Charles’s Law Practice •

Gay-Lussac’s Law • Joseph Louis Gay. Lussac (1778 -1850) Cooled Heated

Gay-Lussac’s Law Practice •

Combined Gas Law •

Combined Gas Law • Example 2: A sample of Helium gas occupies 10. 0 m. L of space at 1. 30 atm and 35. 0 o. C. How much space will this gas occupy at STP? • 11. 5 m. L • Example 3: A reaction between hydrogen gas and nitrogen gas produced 1590 m. L of gaseous ammonia under 289 torr and at a temperature of 125 o. C. What is the volume of ammonia at STP? • 1120 m. L • Example 4: Suppose that 120. m. L of argon is collected over water at 25. 0 o. C and 780. 0 torr. Calculate the volume of the dry argon at STP. • 109 m. L

Ideal Gas Law •

Ideal Gas Law Practice PV= n. RT • (1)V= (1) (0. 0821)(273) V= 22. 4 L

Ideal Gas Law Practice PV= n. RT • (1. 25)(25. 0)= (2. 10) (0. 0821)T T= 181 K

Gas Stoichiometry and Ideal Gas Law • At STP 1 mole of gas occupies 22. 4 L of space. • 22. 4 L can be used as a conversion factor if the reaction occurs at STP. • If a reaction does NOT happen at STP, 22. 4 L cannot be used as a conversion factor • Instead use stoichiometry to find moles of gas, and then use the ideal gas law to determine volume • OR use ideal gas law to find moles, and then use stoichiometry • Example 1: How many liters of hydrogen gas can be collected at 295 K and a pressure of 1. 20 atm if 45. 0 g of liquid ammonia decomposes? 2 NH 3 (l) 3 H 2 (g) + N 2 (g) 45. 0 g NH 3 1 mole NH 3 3 mole H 2 17. 04 g NH 3 2 mole NH 3 = 3. 96 mole H 2 PV = n. RT (1. 20) V = (3. 96) (0. 0821)(295) V = 79. 9 L

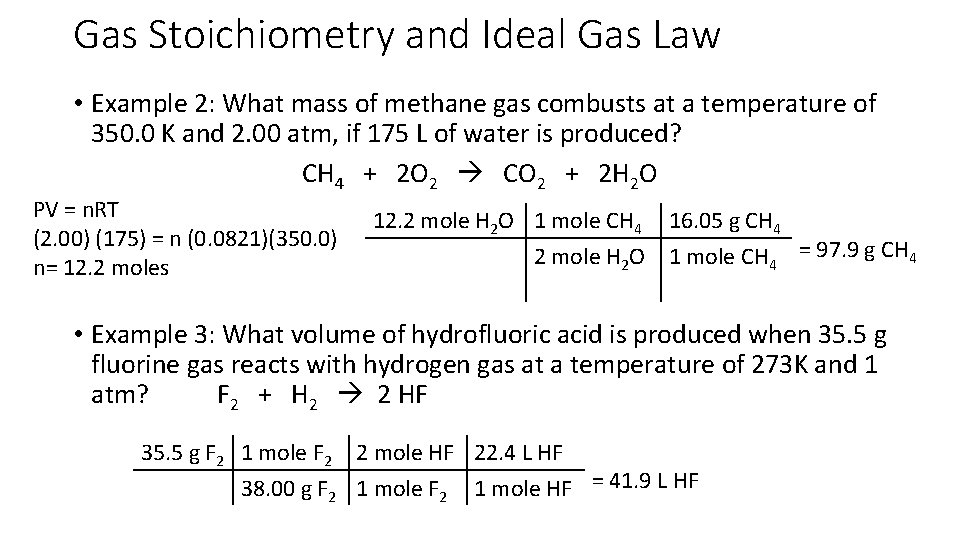
Gas Stoichiometry and Ideal Gas Law • Example 2: What mass of methane gas combusts at a temperature of 350. 0 K and 2. 00 atm, if 175 L of water is produced? CH 4 + 2 O 2 CO 2 + 2 H 2 O PV = n. RT (2. 00) (175) = n (0. 0821)(350. 0) n= 12. 2 moles 12. 2 mole H 2 O 1 mole CH 4 16. 05 g CH 4 2 mole H 2 O 1 mole CH 4 = 97. 9 g CH 4 • Example 3: What volume of hydrofluoric acid is produced when 35. 5 g fluorine gas reacts with hydrogen gas at a temperature of 273 K and 1 atm? F 2 + H 2 2 HF 35. 5 g F 2 1 mole F 2 2 mole HF 22. 4 L HF 38. 00 g F 2 1 mole HF = 41. 9 L HF

Gas Stoichiometry • When gases react, the do so in volumes that are proportional to one another if temperature and pressure remain constant in a reaction. • These proportions are equal to the mole ratio • When converting from volume to volume in stoichiometry, a volume ratio (instead of a mole ratio) can be used. • Example 4: How many liters of ammonia are produced from the reaction of nitrogen gas with 25. 0 L of hydrogen gas? N 2 (g) + 3 H 2 (g) 2 NH 3 (g) 25. 0 L H 2 2 L NH 3 3 L H 2 = 16. 7 L NH 3

Gas Stoichiometry • Example 5: How many liters of oxygen gas are produced from the decomposition of 340. 0 L water vapor? 2 H 2 O (g) 2 H 2 (g) + O 2 (g) 340. 0 L H 2 O 1 L O 2 2 L H 2 O = 170. 0 L O 2

Summary Of Gas Laws Name Law/ Equation Relationship between variables (direct or inverse) Variables held constant Avogadro’s Law Boyle’s Law Charles’s Law Gay-Lussac’s Law Combined Gas Law X Type of container (flexible or rigid) Graham’s Law X X Dalton’s Law of Partial Pressure= Ideal Gas Law= How do you know when to use ideal gas law? Universal Gas Constant (R): How do you know when to use 22. 4 L in stoichiometry?

Unit 13 Formula Sheet Units of pressure @ STP: = 1 atmosphere = 760 mm Hg = 760 torr = 29. 92 inches Hg = 14. 7 pounds/in 2 (psi) = 101. 3 k. Pa = about 34 feet of water