Unit 1 Whole Numbers PLACE VALUE n The

Unit 1 Whole Numbers

PLACE VALUE n The value of any digit depends on its place value n Place value is based on multiples of 10 as follows: HUNDRED TEN MILLIONS THOUSANDS HUNDREDS TENS UNITS 2 , 5 3 7 , 6 1 5 2

EXPANDED FORM n Place value held by each digit can be emphasized by writing the number in expanded form n The only time “and” should be used in expanded form is in place of a decimal 1, 572. 3 can be written in expanded form as: one thousand five hundred seventy-two and three tenths 3

ROUNDING n Used to make estimates n Rounding Rules: n Determine place value to which the number is to be rounded n Look at the digit immediately to its right n n If digit to right is less than 5, replace that digit and all following digits with zeros If digit to right is 5 or more, add 1 to the digit in the place to which you are rounding. Replace all following digits with zeros 4

ROUNDING EXAMPLES n Round 674 to the nearest ten n 7 is in tens place value, so look at 4 n Since 4 is less than 5, leave the 7 alone and replace the 4 with a zero n Ans: 670 n Round 68, 753 to the nearest thousand n 8 is in thousands place value, so look at 7 n Since 7 is greater than 5, raise 8 to 9 and replace 7, 5, and 3 with zeros n Ans: 69, 000 5

ADDITION n Align numbers to be added as shown; line up digits that hold the same place value 1 1538 + 2136 367 4 – Add digits holding same place value, starting on right 8 + 6 = 14 – Write 4 in units place value and carry the one – Continue adding from right to left 6

SUBTRACTION n Align number to be subtracted under the other number as shown; line up digits that hold the same place value 5837 – 654 5183 – Start at the right and work left: 7 – 4 = 3 – Since 5 cannot be subtracted from 3, you need to borrow from 8 (making it 7) and add 10 to 3 (making it 13) – Now, 13 – 5 = 8; 7 – 6 = 1; 5– 0=5 and 7

MULTIPLICATION n Write numbers to be multiplied as shown; line up digits that hold the same place value 2153 × 345 10765 8612 6459 742785 – First, multiply by units digit (5) Write product, starting at units position and going from right to left – Multiply by tens digit (4) Write product, starting at tens position and going from right to left – Follow same procedure with hundreds digit (3) – Add to obtain final product 8

DIVISION n Write division problem with divisor outside long division symbol and dividend within symbol 54 r 6 125 10 6 100 6 • 25 does not go into 1 or 13, but will divide into 135 25 = 5; write 5 above the 5 in number 1356 as shown • • • Multiply: 25 × 5 = 125; write this under 135 Subtract: 135 – 125 = 10 Bring down the 6 106 25 = 4; write this above 6 Multiply: 25 × 4 = 100; write this under 106 Subtract: 106 – 100 = 6; this is the remainder 9

ORDER OF OPERATIONS n All arithmetic expressions must be simplified using the following order of operations: 1. 2. 3. Parentheses Multiplication and division from left to right Addition and Subtraction from left to right Evaluate: (9 + 4) × 16 – 8 = 13 × 16 – 8 = 208 – 8 = 200 Ø Do the operation in parentheses first Ø Multiply next Ø Subtract last 10

ORDER OF OPERATIONS n “PEMDAS” or “Please Excuse My Dear Aunt Sally” are other pneumonic ways to recall. 1. 2. 3. 4. 5. 6. Parenthsis Exponents Multiply Divide Add Subtract Worked left to right if all that is left in the problem 11

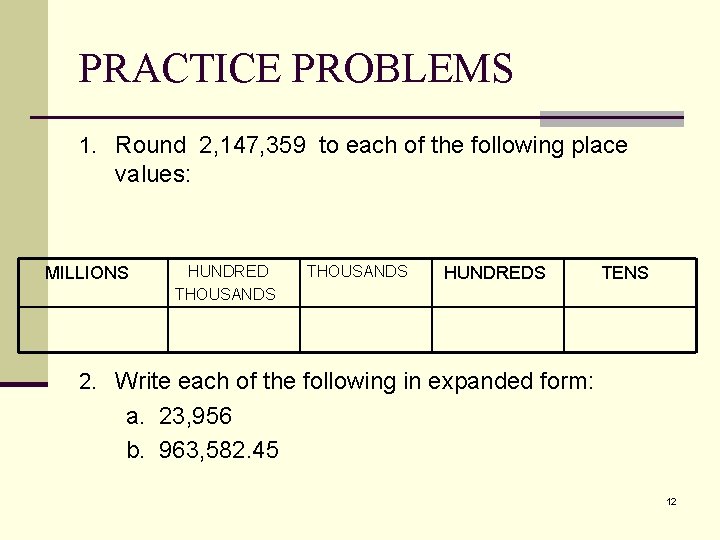
PRACTICE PROBLEMS 1. Round 2, 147, 359 to each of the following place values: MILLIONS HUNDRED THOUSANDS HUNDREDS TENS 2. Write each of the following in expanded form: a. 23, 956 b. 963, 582. 45 12

PRACTICE PROBLEMS (Cont) 3. Perform each of the following operations (round to the thousandth if necessary): 3. 4. a. 1472 + 259 b. 27586 + 98764 c. 2712 – 1659 d. 15784 – 9896 3. 4. e. 158 × 47 f. 4857 × 584 g. h. 13

PRACTICE PROBLEMS (Cont) 4. Evaluate each of the following: a. (5 + 1) × 3 + (2 + 4) b. 7 + 3(4 – 2) c. 27 + 3(4 – 3)(12 + 6) 9 d. 35 – 10 + 6 14

Solutions 1. Rounding 1. 2, 000 2. 2, 100, 000 3. 2, 147, 000 4. 2, 147, 400 5. 2, 147, 360 2. Expanding 1. Twenty three thousand nine hundred fiftysix 2. Nine hundred sixty three thousand five hundred eighty two and forty-five hundredths 15

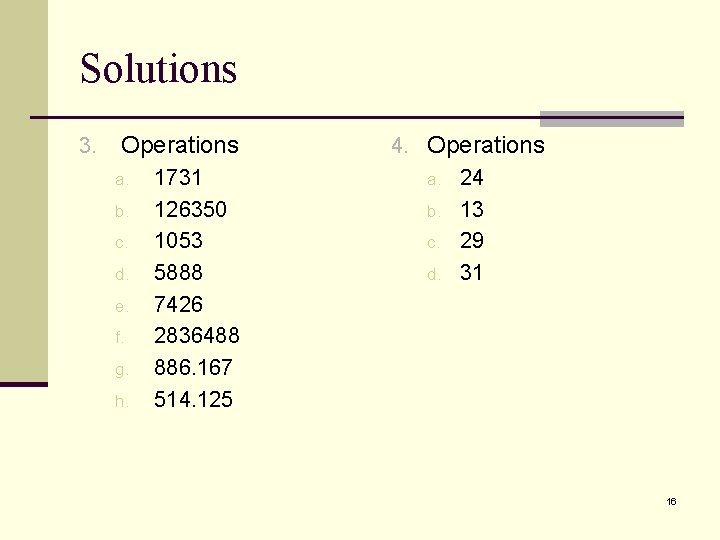
Solutions 3. Operations a. b. c. d. e. f. g. h. 1731 126350 1053 5888 7426 2836488 886. 167 514. 125 4. Operations a. 24 b. 13 c. 29 d. 31 16