Unit 1 Review 1 1 Expressions and formulas








- Slides: 9

Unit 1 Review

1 -1 Expressions and formulas -Order of Operations (ex. #11) -Evaluate expressions (ex. #15)

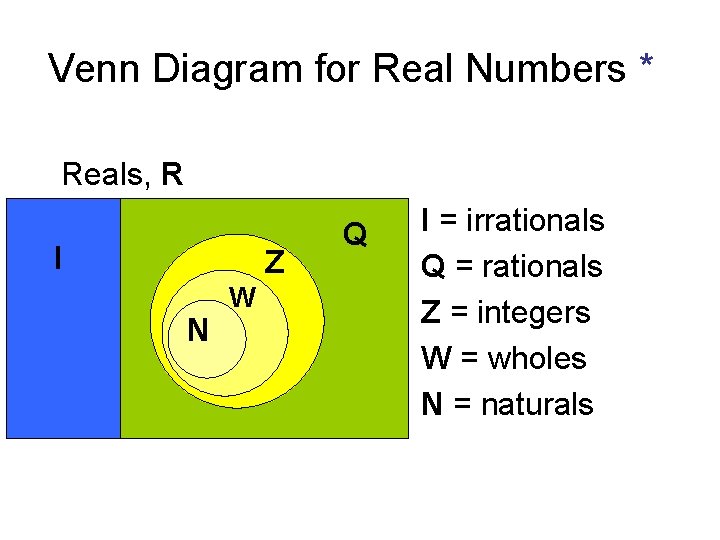
Venn Diagram for Real Numbers * Reals, R I Z N W Q I = irrationals Q = rationals Z = integers W = wholes N = naturals

Properties of Real Numbers** For any real numbers a, b, and c Addition Commutative a + b = b + a Multiplication a(b) = b(a) Associative (a + b)+c =a+(b + c) (ab)c = a(bc) Identity a+0=a=0+a Inverse a + (-a) = 0 = -a + a a(1/a) =1= (1/a)a Distributive a(b + c)= ab + ac & a(b - c)= ac – ac a(1) = a = 1(a)

Writing Algebraic Expressions** a. 2 more than 4 times the cube of a number. b. The quotient of 5 less than a number and 12. 1 A: the cube of a number increase by 4 times the same number 1 B: three time the difference of a number and 8

S. G. I. R. S. G. I. R. implify the expression. (distribute, simplify fractions and decimals) roup the variables onto one side (the left) of the equation using ADDITION and SUBTRACTION. solate the variable. Group all non-variable terms (numbers) to the opposite side (the right side) using ADDITION and SUBTRACTION. emove the coefficient. Once the variable is isolated the last step is to remove the coefficient. DIVIDE both sides by the coefficient, or MULTIPLY both sides by the reciprocal of the coefficient.

Steps for Solving an Absolute Value Equation** • ISOLATE the absolute value!!!! (get the absolute value by itself) • Set up two cases (define a positive and a negative case) • Solve each case (you should get two different solutions) • Check the solution for each case (make sure each solution works)

Graphing inequalities* • Graph one variable inequalities on a number line. • < and > get open circles • < and > get closed circles • For > and > the graph goes to the right. (if the variable is on the left-hand side) • For < and < the graph goes to the left. (if the variable is on the left-hand side)

Absolute Value Inequalities* Steps for solving absolute value inequalities: 1. Isolate the absolute value 2. set up two cases (positive and negative). Remember: < and < are intersections (and) > and > are unions (or) 3. Solve each case 4. Put the solution in a solution set