Unit 1 Program Linear A Sistem Pertidaksamaan Linear

Unit 1 Program Linear A. Sistem Pertidaksamaan Linear Dua Variabel B. Program Linear Matematika untuk kelas XI Sekolah Menengah Atas Kelompok Waib

Diskusi Dalam kehidupan sehari-hari, banyak permasalahan yang melibatkan pengoptimalan, seperti meminimumkan ongkos atau memaksimalkan laba. Bersama teman sebangkumu, carilah satu permasalahan dalam kehidupan sehari yang melibatkan pengoptimalan. Kemudian, selesaikan dengan menggunakan program linear, dan presentasikan hasilnya di depan kelas.

Bersyukurlah karena Tuhan begitu sempurna menciptakan otak manusia sehingga mampu memikirkan konsep-konsep untuk memecahkan masalah sehari-hari bahkan yang rumit sekalipun.

A. Algoritma Pembagian Polinomial 1. Persamaan Linear Dua Variabel

Contoh Soal 1. 1 Penyelesaian Persamaan Linear Dua Variabel • Penyelesaian •

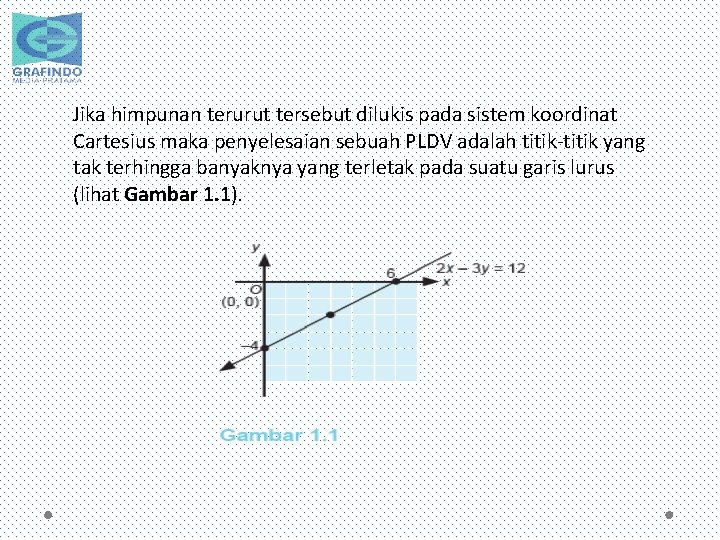
Jika himpunan terurut tersebut dilukis pada sistem koordinat Cartesius maka penyelesaian sebuah PLDV adalah titik-titik yang tak terhingga banyaknya yang terletak pada suatu garis lurus (lihat Gambar 1. 1).

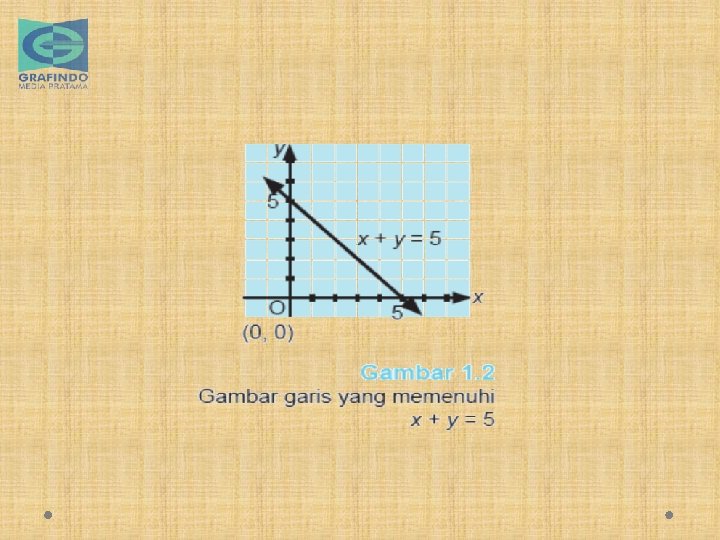
Untuk menggambar suatu garis hanya diperlukan dua pasangan terurut (dua titik) yang memenuhi persamaan garis tersebut. Agar lebih mudah, biasanya titik pertama diambil titik potong terhadap sumbu-x (memiliki y = 0) dan titik kedua diambil titik potong terhadap sumbu-y (memiliki x = 0).

Contoh Soal 1. 2

3. Pertidaksamaan Linear Dua Variabel Pertidaksamaan linear dua variabel mirip seperti persamaan linear dua variabel, hanya saja sebagai pengganti tanda ''='' digunakan salah satu dari tanda ketidaksamaan, yaitu: ''>, ≥, <, atau ≤''. Bentuk Umum Pt. LDV ax + by < c atau ≤ c atau > c atau ≥ c dengan a, b, c, ∈ R dan a, b keduanya tidak nol, sedangkan x dan y sebagai variabel.

Contoh Soal 1. 3 Menentukan Daerah yang Memenuhi Pt. LDV Tentukan daerah penyelesaian 2 x + 3 y ≤ 12.

Langkah 2. • Garis batas 2 x + 3 y = 12 membagi gambar menjadi dua daerah, yaitu daerah I (daerah di atas garis 2 x + 3 y = 12) dan daerah II (daerah di bawah garis 2 x + 3 y = 12). • Ambilah satu titik sebarang yang tidak terletak pada garis sebagai titik uji. Jika titik uji memenuhi Pt. LDV (2 x + 3 y ≤ 12) maka daerah titik uji ini memenuhi Pt. LDV. Kemudian, daerah ini diwarnai.

Jika titik uji tidak memenuhi Pt. LDV (2 x + 3 y ≤ 12) maka daerah titik uji tidak memenuhi Pt. LDV. Hal ini berarti daerah yang memenuhi Pt. LDV adalah daerah di seberang titik uji, dan daerah inilah yang diwarnai. Untuk mempermudah perhitungan, titik asal (0, 0) diambil sebagai titik uji, asalkan titik (0, 0) tidak terletak pada garis batas. Dalam kasus pada Gambar 1. 3, titik (0, 0) tidak terletak pada garis batas persamaan 2 x + 3 y = 12. Dengan demikian, titik (0, 0) dapat diambil sebagai titik uji dari Pt. LDV 2 x + 3 y ≤ 12. Titik uji (0, 0) 2(0) + 3(0) = 0 ≤ 12 (memenuhi). Oleh karena (0, 0) memenuhi 2 x + 3 y ≤ 12 maka daerah II yang mengandung titik uji (0, 0) adalah daerah yang memenuhi 2 x + 3 y ≤ 12. Oleh karena itu, daerah II diwarnai (Gambar 1. 4).

Langkah-Langkah untuk Menggambar Daerah yang Memenuhi Suatu Pertidaksamaan Linear Dua Variabel 2 1 Ganti notasi ketidaksamaan dengan tanda sama dengan (''=''). Pada sumbu Cartesius gambarlah garis yang memenuhi persamaan linear dua variabel. Jika dalam Pt. LDV terdapat tanda ''≤ atau ≥'', gambarlah garis tersebut sebagai garis utuh. Akan tetapi, jika tanda dalam Pt. LDV adalah ''< atau >'', gambarlah garis tersebut dengan garis putus-putus. Garis ini sebagai garis batas yang akan membagi bidang koordinat x – y menjadi dua daerah. Pilih satu titik uji sebarang. Lebih memudahkan perhitungan jika titik (0, 0) diambil sebagai titik uji dalam Pt. LDV. a. Jika koordinat titik uji memenuhi Pt. LDV maka daerah yang mengandung titik uji memenuhi Pt. LDV dan daerah ini diarsir atau diwarnai. b. Jika koordinat titik uji tidak memenuhi Pt. LDV maka daerah yang mengandung titik uji tidak memenuhi Pt. LDV. Ini berarti daerah yang memenuhi adalah daerah di seberang titik uji, dan daerah inilah yang diarsir atau diwarnai.

4. Sistem Pertidaksamaan Linear Dua Variabel Sebuah pabrik roti memproduksi dua jenis roti, yaitu isi cokelat dan isi keju. Pembuatan roti isi cokelat memerlukan 6 gram terigu dan 5 gram mentega, sedangkan untuk roti isi keju diperlukan 4 gram terigu dan 5 gram mentega. Bahan yang tersedia adalah 2. 400 gram terigu dan 2. 500 gram mentega. Informasi ini dapat disajikan, seperti pada Tabel 1. 1. Dari Tabel 1. 1 dibuat model matematikanya, yaitu Bentuk (*) dinamakan sistem pertidaksamaan linear dua variabel (disingkat SPt. LDV)

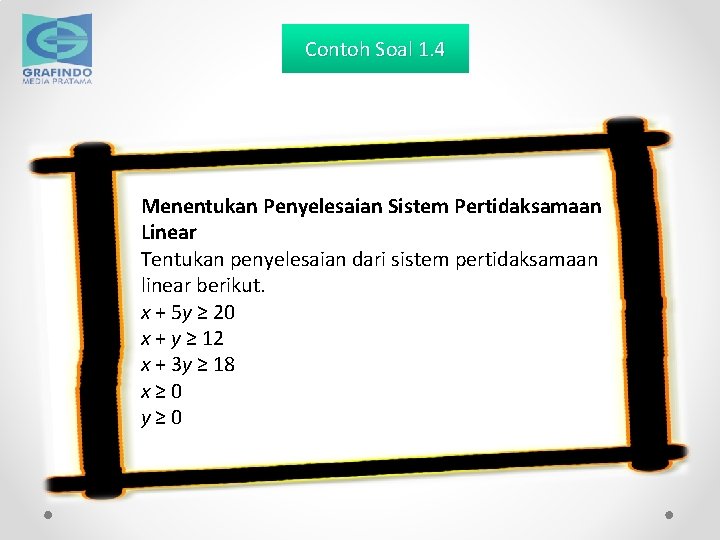
Contoh Soal 1. 4 Menentukan Penyelesaian Sistem Pertidaksamaan Linear Tentukan penyelesaian dari sistem pertidaksamaan linear berikut. x + 5 y ≥ 20 x + y ≥ 12 x + 3 y ≥ 18 x ≥ 0 y ≥ 0

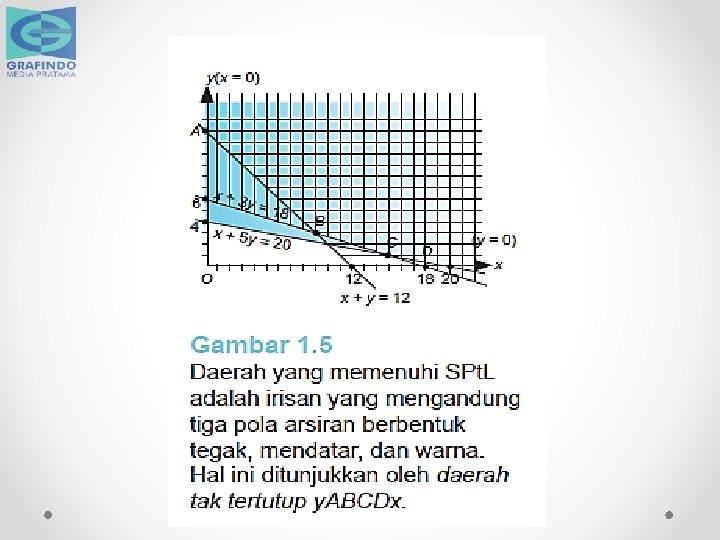
Penyelesaian Lukis kelima garis batas dari sistem pertidaksamaan linear (SPt. L), yaitu: x + 5 y = 20; x + y = 12; x + 3 y = 18; x = 0 (sumbu-y); dan y = 0 (sumbu-x), dengan cara seperti dalam Contoh Soal 1. 2. Hal ini ditunjukkan pada Gambar 1. 5. 1 Tentukan daerah yang memenuhi setiap Pt. LDV dari SPt. L dengan cara seperti dalam Contoh Soal 1. 3. Arsir setiap daerah yang memenuhi dengan pola arsiran yang berbeda. Supaya arsiran Anda tidak rumit, daerah yang memenuhi x ≥ 0 dan y ≥ 0, yaitu daerah dalam kuadran pertama, tidak perlu diarsir. Hal ini ditunjukkan pada Gambar 1. 5. 2 Daerah yang memenuhi SPt. L adalah daerah dalam kuadran pertama (memenuhi x > 0 dan y > 0) yang memiliki tiga pola arsiran berbeda. Daerah ini adalah daerah tidak tertutup y. ABCDx dalam Gambar 1. 5. 3

Langkah-Langkah untuk Menentukan Daerah yang Memenuhi Sistem Pertidaksamaan Linear Langkah 1. Lukis setiap garis dari PLt. DV yang diberikan dalam masalah SPt. L. Langkah 2. Dengan menggunakan satu titik uji (biasanya titik (0, 0)), tentukan daerah yang memenuhi setiap Pt. LDV. Beri tanda daerah tersebut dengan arsiran. Langkah 3. Tentukan daerah yang memenuhi SPt. L, yaitu daerah yang merupakan irisan dari daerah-daerah yang memenuhi tiap Pt. LDV dalam Langkah 2.

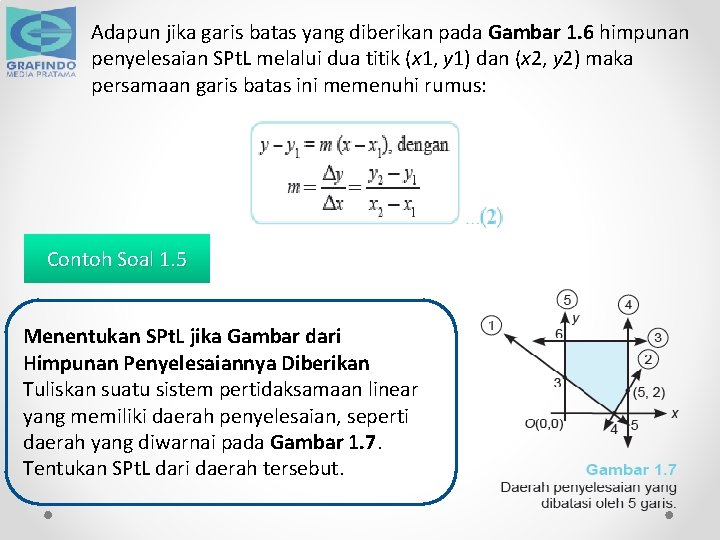
5. Menentukan Sistem Pertidaksamaan Linear jika Gambar Himpunan Penyelesaian Diberikan a. Persamaan Garis jika Titik Potong Garis terhadap Sumbu-Sumbu Koordinat Diberikan Jika garis batas yang diberikan pada gambar himpunan penyelesaian SPt. L memotong sumbu koordinat di titik-titik (0, b) dan (a, 0) (perhatikan Gambar 1. 6) maka persamaan garis batas ini memenuhi rumus:

Adapun jika garis batas yang diberikan pada Gambar 1. 6 himpunan penyelesaian SPt. L melalui dua titik (x 1, y 1) dan (x 2, y 2) maka persamaan garis batas ini memenuhi rumus: Contoh Soal 1. 5 Menentukan SPt. L jika Gambar dari Himpunan Penyelesaiannya Diberikan Tuliskan suatu sistem pertidaksamaan linear yang memiliki daerah penyelesaian, seperti daerah yang diwarnai pada Gambar 1. 7. Tentukan SPt. L dari daerah tersebut.

Penyelesaian 1 Daerah yang diwarnai dalam Gambar 1. 7 dibatasi oleh lima garis. 2 Menentukan kelima persamaan garis batas yang telah ditandai dengan nomor (1), (2), (3), (4), dan (5) pada Gambar 1. 7. Garis (1) memotong sumbu-x di (4, 0) dan sumbu-y di (0, 3) sehingga persamaannya memenuhi persamaan (1).

Garis (2) melalui titik (4, 0) dan (5, 2) sehingga memenuhi persamaan (2). Garis (3) adalah garis horizontal melalui (0, 6) sehingga persamaannya adalah y = 6 . . . garis (3) Garis (4) adalah garis vertikal melalui (5, 0) sehingga persamaannya adalah x = 5 . . . garis (4) Garis (5) adalah sumbu y x = 0 . . . garis (5)

3 Tentukan tanda pertidaksamaan dari setiap garis batas (> ataukah <) dengan mengambil satu titik uji tanda dalam daerah penyelesaian (daerah yang diwarnai). Misalnya, ambil P(4, 1), lihat Gambar 1. 7, dan tentukan tanda pertidaksamaan setiap garis batas.

4 Tentukan SPt. L yang ditanyakan. Dari Langkah 3 diperoleh sistem pertidaksamaan linear yang memenuhi daerah yang diwarnai dalam Gambar 1. 7 adalah: 3 x + 4 y ≥ 12; 2 x – y ≤ 8; y ≤ 6; x ≤ 5; x ≥ 0

Latihan Soal Kegiat a n Kerjakan Uji Materi 1. 1 halaman 10, buku Matematika untuk Kelas XI SMA Kelompok Wajib.

B. Program Linear 1. Model Matematika Pembentukan sistem pertidaksamaan linear kedalam persamaan linear dinamakan pemodelan matematika. Di dalam pemodelan matematika untuk masalah program linear terdapat dua macam fungsi, yaitu fungsi tujuan atau fungsi objektif (objective function) dan kendala atau batasan (constraint). Bangkit Karakter Dalam kegiatan sehari-hari dapat Anda aplikasikan pemecahan masalah dengan menggunakan model matematika. Berikan beberapa permasalahan lain secara kreatif yang dapat Anda buat model matematikanya.

Contoh Soal 1. 6 Pemecahan Masalah dengan Menggunakan Model Matematika Sebuah pabrik roti memproduksi dua jenis roti, yaitu roti isi cokelat dan roti isi keju. Pembuatan satu buah roti isi cokelat memerlukan 6 gram terigu dan 5 gram mentega, sedangkan untuk satu buah roti isi keju memerlukan 4 gram terigu dan 5 gram mentega. Keuntungan roti isi cokelat Rp 550, 00 per buah dan roti isi keju Rp 400, 00 per buah. Bahan yang tersedia adalah 2. 400 gram terigu dan 2. 500 gram mentega. Buatlah model matematika untuk permasalahan tersebut, apabila banyaknya roti isi cokelat x buah dan isi roti keju y buah.

Penyelesaian 1 Barang yang diproduksi adalah dua jenis roti: roti isi cokelat dan roti isi keju. Mulailah dengan pemisalan. Misalkaan, roti isi cokelat yang diproduksi = x buah, roti isi keju yang diproduksi = y buah. Tidak mungkin membuat – 2 roti sebab pernyataan seperti ini tidak bermakna. Dari sini diperoleh dua fungsi kendala yang tak mungkin negatif, yaitu x ≥ 0 dan y ≥ 0.

2 Roti terbuat dari terigu dan mentega sehingga fungsi kendala berikutnya pastilah berkaitan dengan persediaan terigu dan mentega. 1 roti cokelat memerlukan 6 gram terigu dan 5 gram mentega. x roti cokelat memerlukan 6 x gram terigu dan 5 x gram mentega. 1 roti keju memerlukan 4 gram terigu dan 5 gram mentega. y roti keju memerlukan 4 y gram terigu dan 5 y gram mentega. Jadi, terigu yang diperlukan adalah (6 x + 4 y) gram dan mentega yang diperlukan adalah (5 x + 5 y) gram. Persediaan terigu = 2. 400 gram sehingga Pt. LDVnya adalah 6 x + 4 y ≤ 2. 400. Persediaan mentega = 2. 500 gram sehingga Pt. LDVnya adalah 5 x + 5 y ≤ 2. 500.

3 Fungsi kendala yang diperoleh dari Langkah 1 dan Langkah 2 menghasilkan model matematika sebagai berikut. 6 x + 4 y ≤ 2. 400. . . (1) 5 x + 5 y ≤ 2. 500. . . (2) x ≥ 0. . . (3) y ≥ 0. . . (4)

4 Adapun fungsi tujuan berkaitan dengan keuntungan menjual roti isi cokelat dan roti isi keju. 1 roti isi cokelat memperoleh untung Rp 550, 00. x roti isi cokelat memperoleh untung 550 x rupiah. 1 roti isi keju memperoleh untung Rp 400, 00. y roti isi keju memperoleh untung 400 y rupiah. Jadi, fungsi tujuan adalah = 550 x + 400 y. Fungsi tujuan inilah yang biasanya dimaksimumkan atau diminimumkan. Secara ringkas, model matematika program linear dalam masalah pembuatan roti ini dinyatakan dalam Tabel 1. 2 berikut.

2. Menyelesaikan Masalah Program Linear Suatu program linear dalam dua variabel x dan y memiliki satu fungsi tujuan yang dioptimumkan (maksimum atau minimum). Fungsi tujuan biasa diberi notasi z.

Secara umum, setiap masalah program linear memiliki dua komponen, sebagai berikut. 1. Sekumpulan pertidaksamaan linear yang harus dipenuhi secara bersama. 2. Satu fungsi tujuan yang harus dioptimalkan (minimum atau maksimum).

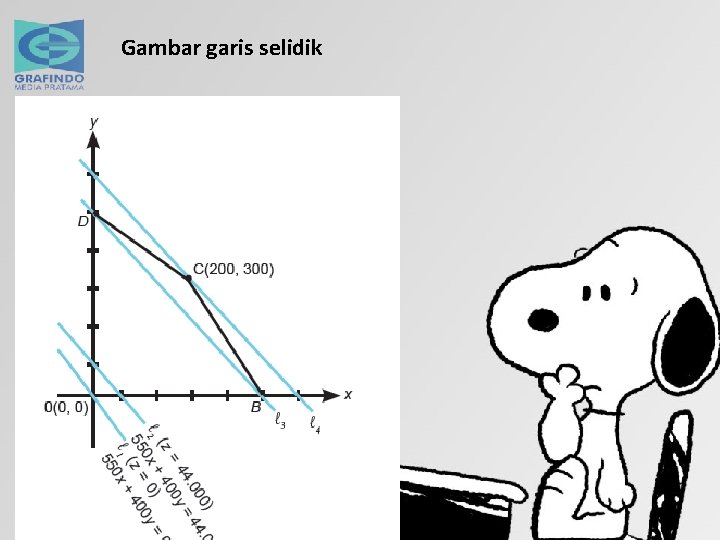
Metode Garis Selidik untuk Menentukan Titik Optimum 1. Untuk masalah memaksimumkan: fungsi tujuan, geser garis selidik primitif ax + by = 0 secara sejajar sampai memotong titik paling jauh dari daerah yang memenuhi sistem pertidaksamaan linear. Titik paling jauh biasanya adalah titik pojok yang paling atas atau paling kanan dari daerah yang memenuhi SPt. L. 2. Untuk masalah meminimumkan: fungsi tujuan, geser garis selidik primitif ax + by = 0 secara sejajar sampai memotong titik paling dekat dari daerah yang memenuhi sistem pertidaksamaan linear. Titik paling dekat biasanya adalah titik pojok paling bawah atau paling kiri daerah yang memenuhi SPt. L.

Gambar garis selidik

Metode Titik Pojok 1. Jika suatu masalah program linear memiliki penyelesaian maka daerah penyelesaiannya akan berada pada titik-titik pojok dari titik-titik yang mungkin. Titik-titik yang mungkin adalah titik yang berada dalam daerah yang memenuhi SPt. L (daerah ini, dalam gambar biasanya diberi warna). 2. Jika suatu masalah program linear memiliki banyak penyelesaian maka paling sedikit suatu penyelesaian akan berada di suatu titik pojok dari grafik titik-titik yang mungkin. Dalam setiap kasus tersebut (kasus (1) dan kasus (2)), nilai fungsi tujuan selalu hanya ada satu.

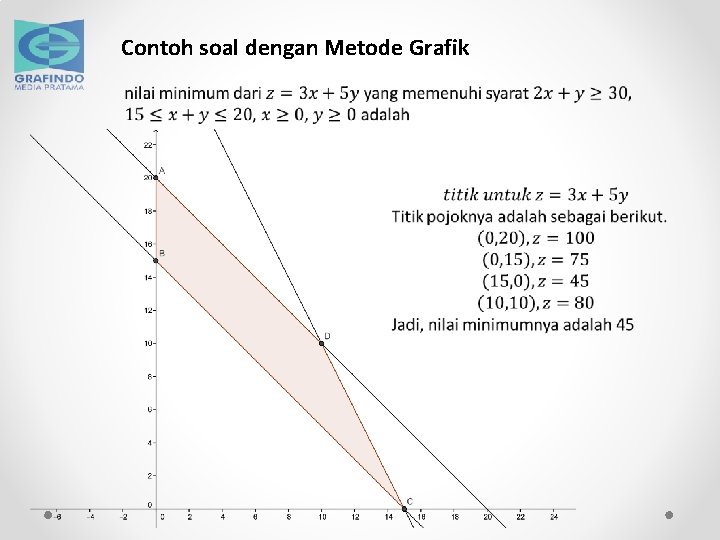
Langkah-Langkah untuk Memecahkan Masalah Program Linear dengan Metode Grafik 1. Menentukan fungsi tujuan dan menyatakannya ke dalam model matematika berupa satu persamaan dengan bentuk umum: z = ax + by, dengan a, b R serta a ≠ 0 dan b ≠ 0. 2. Mengidentifikasi kendala atau batasan serta menyatakannya ke dalam model matematika berupa sekumpulan pertidaksamaan linear dua variabel. 3. Menggambar semua garis pada fungsi kendalam satu koordinat Cartesius. 4. Menentukan daerah himpunan penyelesaian yang memenuhi semua pertidaksamaan linear dalam Langkah 2. Daerah ini biasanya diwarnai (atau diarsir). 5. Menentukan koordinat (x, y) dari semua titik pojok dari daerah yang diwarnai dalam Langkah 4. 6. Menyubstitusi x dan y dari setiap titik pojok dalam Langkah 5 ke dalam fungsi tujuan z = ax + by untuk menentukan nilai z optimum (maksimum atau minimum).

Contoh soal dengan Metode Grafik

Latihan Soal Kegiat an Kerjakan Uji Materi 1. 2 halaman 2122, buku Matematika untuk Kelas XI SMA Kelompok Wajib.

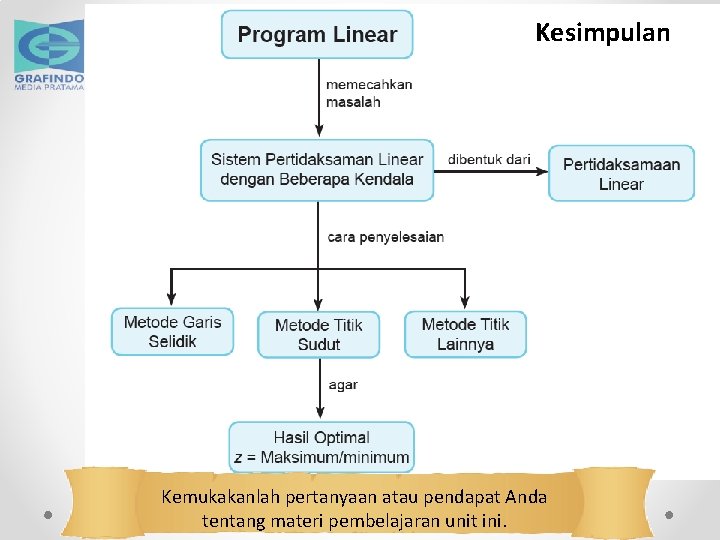
Kesimpulan Kemukakanlah pertanyaan atau pendapat Anda tentang materi pembelajaran unit ini.

Kuis Kegiat a n Kerjakan Uji Kompetensi Unit 1 halaman 23 -24, buku Matematika untuk Kelas XI SMA Kelompok Wajib.

Terima Kasih “tindakan adalah lebih meyakinkan daripada perkataan” John Woolman

referensi • www. jpnn. com • rackcdn. com • www. rendersgraphiques. fr • deviantart. net • www. tipsdancaramasaka. blogspot. com • www. xiibi. com • www. pptbackground. net • www. antaranews. com

Created by Suci Rahayu