Unit 1 Practice Test Answer Key 1 If

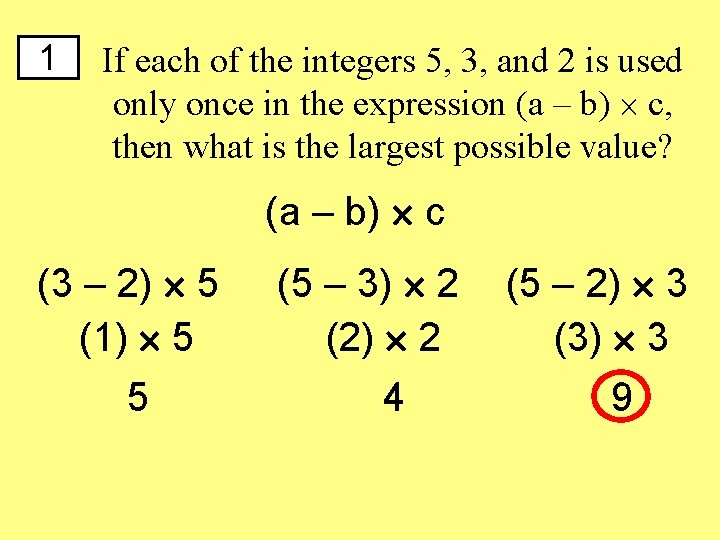




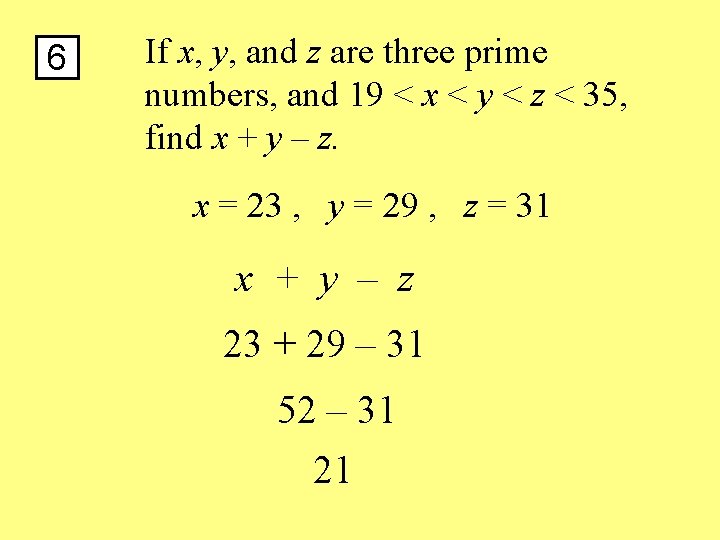













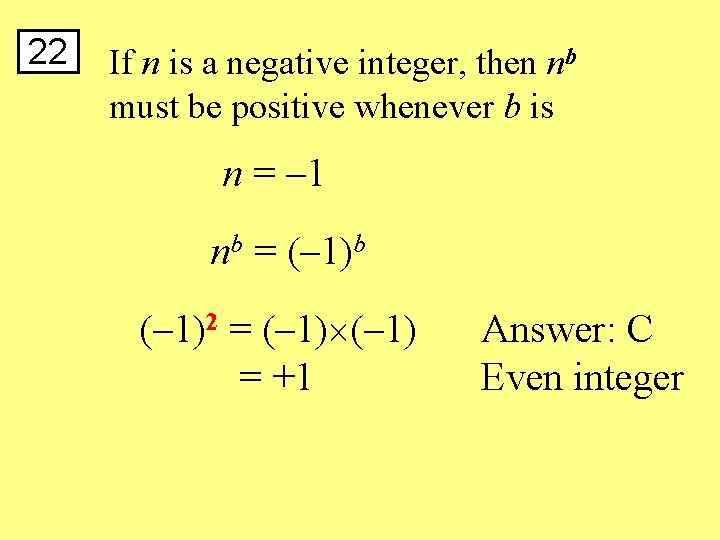
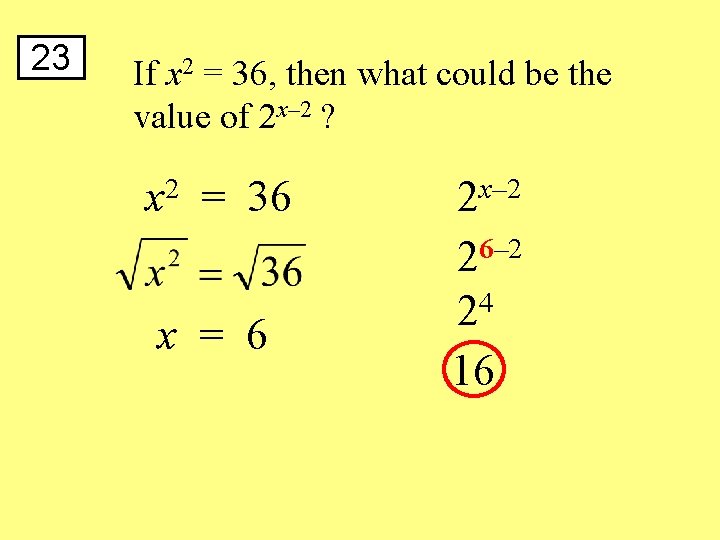



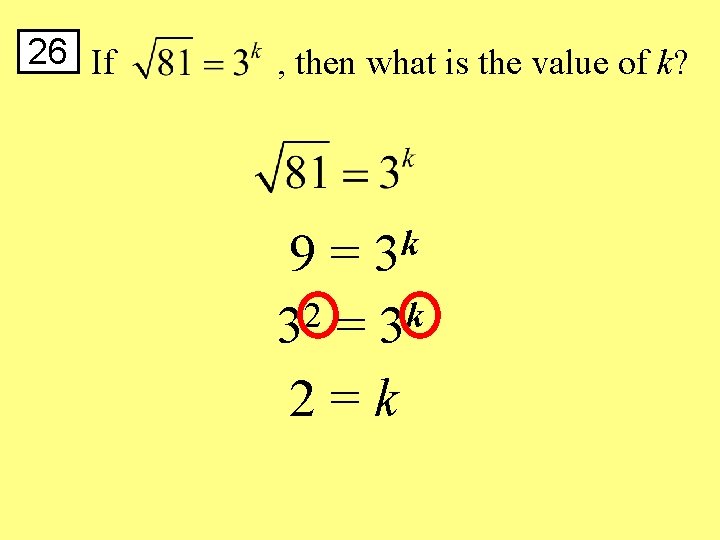
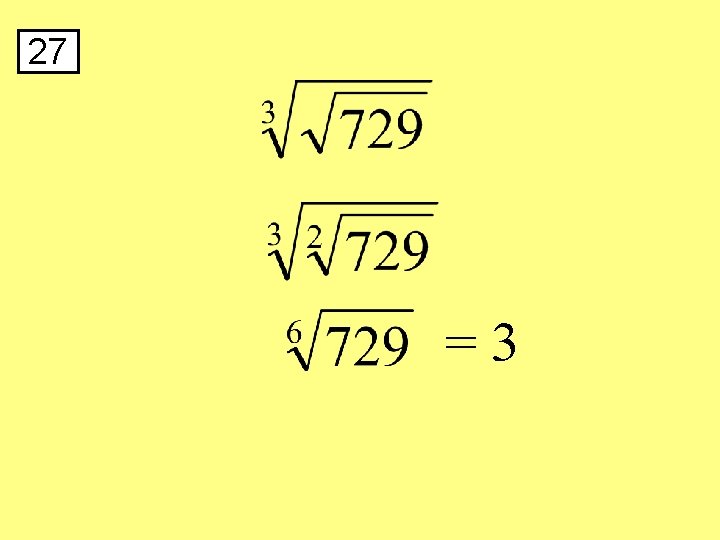





- Slides: 38

Unit 1 Practice Test Answer Key
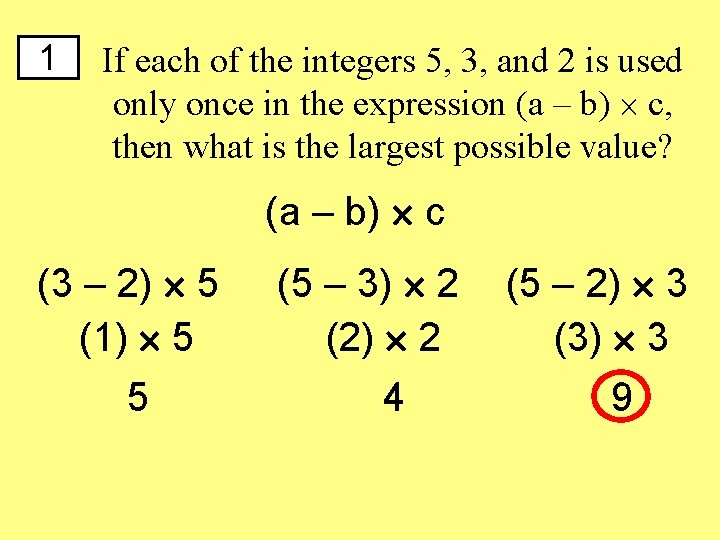
1 If each of the integers 5, 3, and 2 is used only once in the expression (a – b) c, then what is the largest possible value? (a – b) c (3 – 2) 5 (1) 5 5 (5 – 3) 2 (2) 2 4 (5 – 2) 3 (3) 3 9

2 In the correctly worked multiplication problems, L, M, and N are single-digit integers. What is the value of N – M? M=4 L=7 28 N=3 L =7 21 N–M = 3 – 4 = – 1 Factors of 28 and 21 28: 1, 2, 4, 7, 14, 28 21: 1, 3, 7, 21 Greatest Common Factor = 7

If n is a negative integer, what is the ordering of p, t, and r from greatest to least? p = n 2 – 2. 1 ; t = n 3 + 2. 1 ; r = (n – 2. 1)2 3 Substitute: n = – 1 p = (– 1)2 – 2. 1 t = (– 1)3 + 2. 1 r = (– 1 – 2. 1)2 p = 1 – 2. 1 t = – 1 + 2. 1 r = (– 3. 1)2 p = – 1. 1 t = 1. 1 r = 9. 61 r>t>p

4 In a hospital parking lot, the rate is $1. 50 for the first 2 hours and $0. 75 for each additional hour or part of an hour. What does it cost to park a car for 4 hours and 15 minutes? 2 Hours 3 Hours 4 Hours 15 Minutes Total $1. 50 $0. 75 $3. 75

5 P is a two-digit number. Q is a two-digit number, with P’s digits reversed. What is the largest possible value of P so that P and Q fit the given description and also have a difference of 54? Try E. 97 P: 97 Q: 79 Difference 97 – 79 = 18 Try D. 96 P: 96 Q: 69 96 – 69 = 27 Try C. 93 P: 93 Q: 39 93 – 39 = 54 YES NO NO
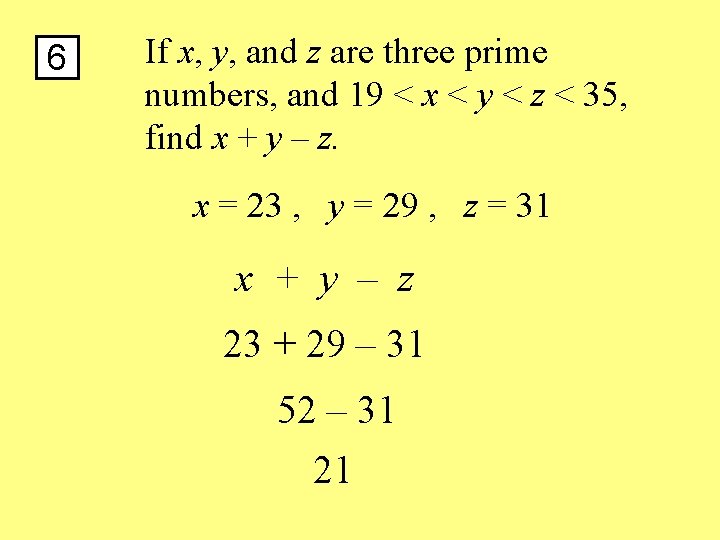
6 If x, y, and z are three prime numbers, and 19 < x < y < z < 35, find x + y – z. x = 23 , y = 29 , z = 31 x + y – z 23 + 29 – 31 52 – 31 21

7 If N is an odd or even integer, which of the following will always be an odd integer? Substitute odd integer Substitute even integer 2(3) + 1 2(4) + 1 8+1 6+1 9 7 Answer: 2 N + 1

8 If m and p are positive integers, which expression must be negative? Substitute: m = 2 A. m – p 2 – 5 = – 3 B. p – m 5– 2=3 C. m + p No p=5 Subtraction with positive numbers can be positive or negative 2 + 5 = 7 No D. –(m + p) –(2 + 5) = – 7 Yes E. –(m – p)

9 What is the value of x for which ? Rewrite the fractions as decimals. Test A. NO Test B. NO Test C. YES

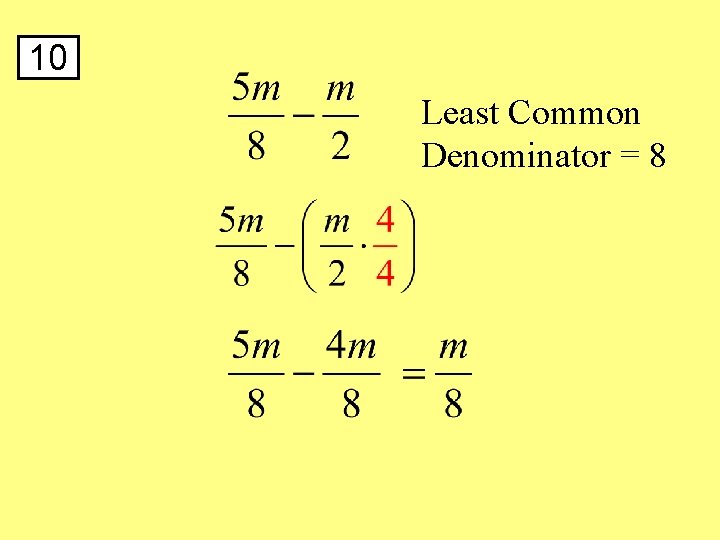
10 Least Common Denominator = 8

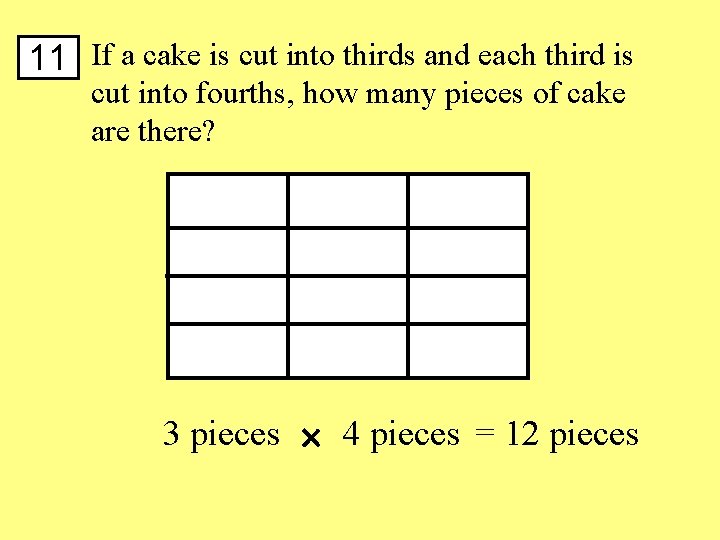
11 If a cake is cut into thirds and each third is cut into fourths, how many pieces of cake are there? 3 pieces 4 pieces = 12 pieces

12 Amy spent of the money in her savings account on clothes. The next month she spent of the remainder of her money on a weekend in Montauk. If she then had $3, 600 left, how much was in her savings account originally? Strategy: Multiply each answer times. Find amount remaining. Multiply remaining amount times. Find remaining amount. It should equal $3, 600.

12 Amy spent of the money in her savings account on clothes. The next month she spent of the remainder of her money on a weekend in Montauk. If she then had $3, 600 left, how much was in her savings account originally? Test C. $4, 900 Test E. $6, 000 4, 900 – 980 = 3, 920 6, 000 – 1200 = 4, 800 3, 920 – 980 = 2940 No 4800 – 1200 = 3600 Yes

13 There are b boys and g girls at the Jericho Academy. Girls make up what fractional part of the student body? Assume there are 8 girls and 5 boys.

15 If D is a nonzero digit in the decimal number 0. 0 D, which of the following must be equal to Substitute any number for D. Then, find the answer that is equal to the same result. (A) ?

16 If it takes ½ hour to wash a car, how many days will it take to wash 96 cars? Time ½ hour 1 hour 2 hours 24 hours 1 day 2 days Number of Cars 1 2 1 = 2 2 2 = 4 2 24 = 48 48 2 48 = 96 96 48 = 2 days

17 If 8 is 8% of N, then what does N equal? Test each answer. Substitute for N. A. 1 8% of 1 =. 08 1 = 0. 08 No B. 8 8% of 8 =. 08 8 = 0. 64 No C. 10 8% of 10 =. 08 10 = 0. 8 No D. 80 8% of 80 =. 08 80 = 6. 4 No E. 100 8% of 100 =. 08 100 = 8 Yes

18 Kathy, Keri, and Kim raised $10, $15, and $25 respectively, during a fundraising drive. What percent of the money did Kathy raise? Total raised = $10 + $15 + $25 = $50 Percent Kathy raised = 0. 2 100 = 20%

19 If the average cost of making five copies on a copy machine has increased from 18ȼ to 20ȼ, what was the percent increase? Amount of Increase = 20¢ – 18¢ = 2¢ = 0. 11 100 = 11%

20 If a $3. 75 book was bought for $3. 30, what was the percent discount? Original Sale Discount = Price – Price Discount = $3. 75 – $3. 30 = $0. 45 = 0. 12 100 = 12%

21 A CD player costs the store $270. If the store must make a 23% profit, what must be the selling price? Profit = 23% of $270 =. 23(270) = 62. 10 Selling Purchase + Profit = Price + $62. 10 = $270 = $332. 10
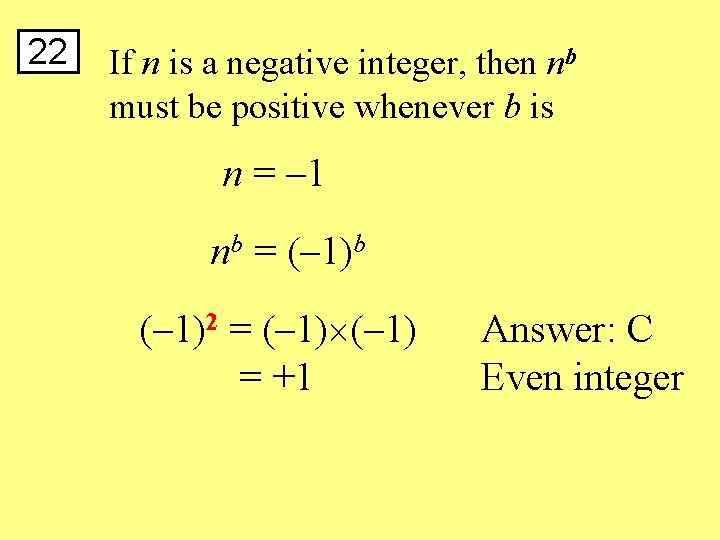
22 If n is a negative integer, then nb must be positive whenever b is n = – 1 nb = (– 1)b (– 1)2 = (– 1) = +1 Answer: C Even integer
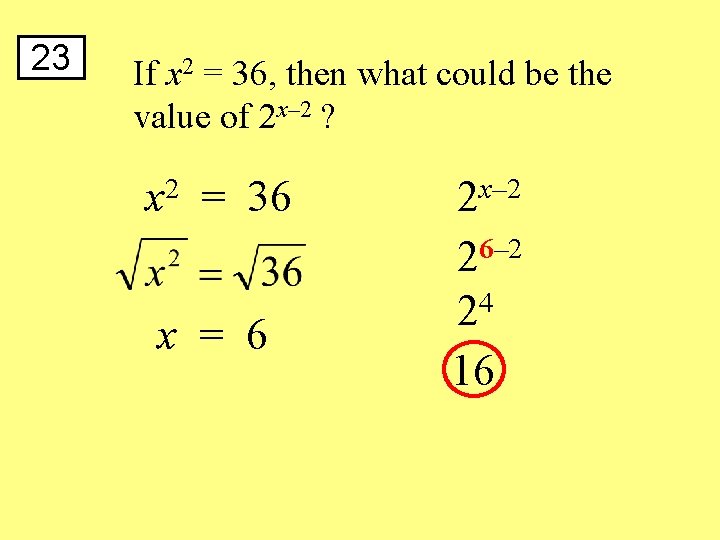
23 If x 2 = 36, then what could be the value of 2 x– 2 ? x 2 = 36 x = 6 2 x– 2 26– 2 4 2 16

24 x, y, and z are three consecutive integers and z > y > x. If z = x 2, which of the following could be the value of x? I. 2 II. 0 III. – 1 Test x = 2 Test x = 0 z = 22 z=4 z = 02 z=0 x<y<z 2<3<4 x<y<z 0<y<0 Test x = – 1 z = (– 1)2 z=1 x<y<z – 1 < 0 < 1

25 If a and b are positive integers such that a 2 = 25 and b 2 = 36. Which of the following statements are true? I. a + b = 61 II. b – a = 1 III. a b = 30 Find a and b. a 2 = 25 b 2 = 36 a =5 b =6

25 If a and y are positive integers such that a 2 = 25 and b 2 = 36. Which of the following statements are true? a =5 b =6 I. a + b = 61 II. b – a = 1 III. a b = 30 5 + 6 = 61 11 61 6– 5=1 1=1 5 6 = 30 30 = 30 No Yes Answer: D Only II and III Yes
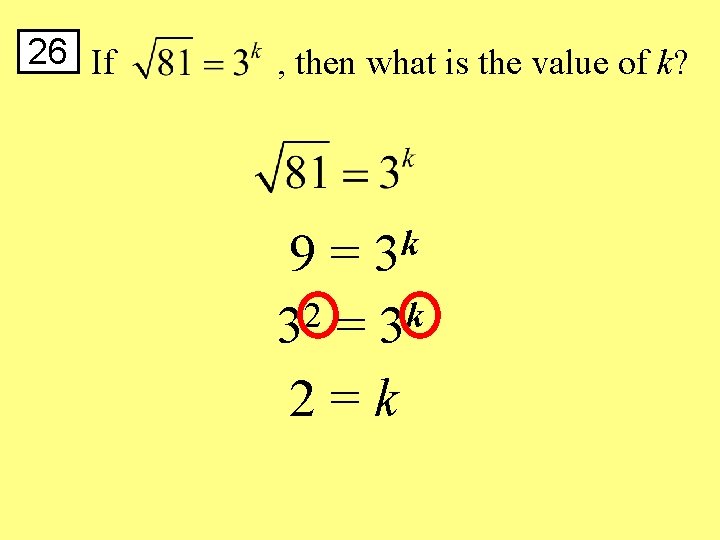
26 If , then what is the value of k? k 3 9= 2 k 3 =3 2=k
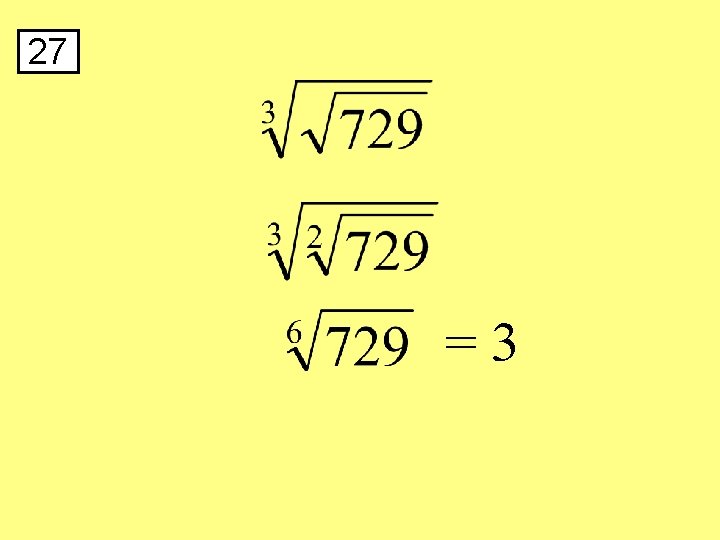
27 =3

28 is a number that lies between which two powers of 10. 102 100 103 1, 000 Answer: B

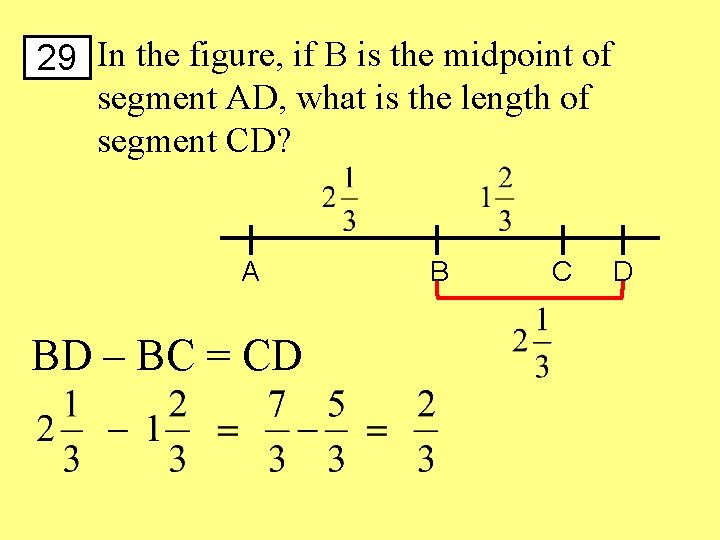
29 In the figure, if B is the midpoint of segment AD, what is the length of segment CD? A BD – BC = CD B C D

30 In the figure, points B and C divide the segment AD into three equal parts. BC is what percent of AC? 4 4 4 Substitute a number for the lengths of each line segment. = 0. 5 100 = 50%

31 In the figure, the tick marks are equally spaced and their coordinates are shown. Of these coordinates, which has the smallest positive value? – 8 a b – 5 – 2 Number of units from the first to the last peg 10 – (– 8) = 10 + 8 = 18 c 1 d 4 e 7 10 Number of pegs after the first peg: 6 How many units are the pegs apart? 18 6 = 3

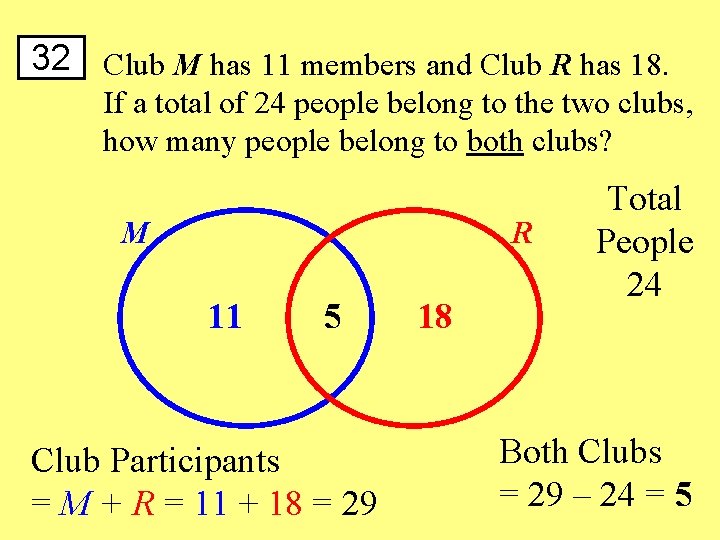
32 Club M has 11 members and Club R has 18. If a total of 24 people belong to the two clubs, how many people belong to both clubs? M R 11 5 Club Participants = M + R = 11 + 18 = 29 18 Total People 24 Both Clubs = 29 – 24 = 5

33 There are 18 boys in the class: 6 play football, 5 play baseball, and 3 play on both teams. How many boys are not on either team? Football 6 Baseball 3 5

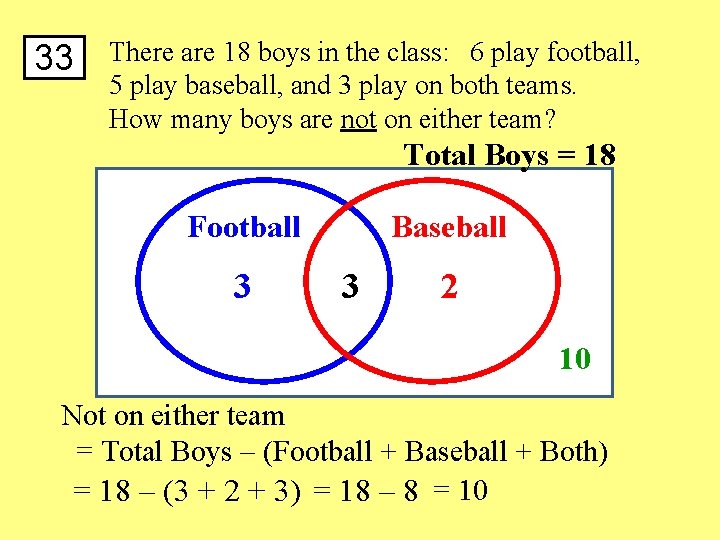
33 There are 18 boys in the class: 6 play football, 5 play baseball, and 3 play on both teams. How many boys are not on either team? Total Boys = 18 Football 3 Baseball 3 2 10 Not on either team = Total Boys – (Football + Baseball + Both) = 18 – (3 + 2 + 3) = 18 – 8 = 10

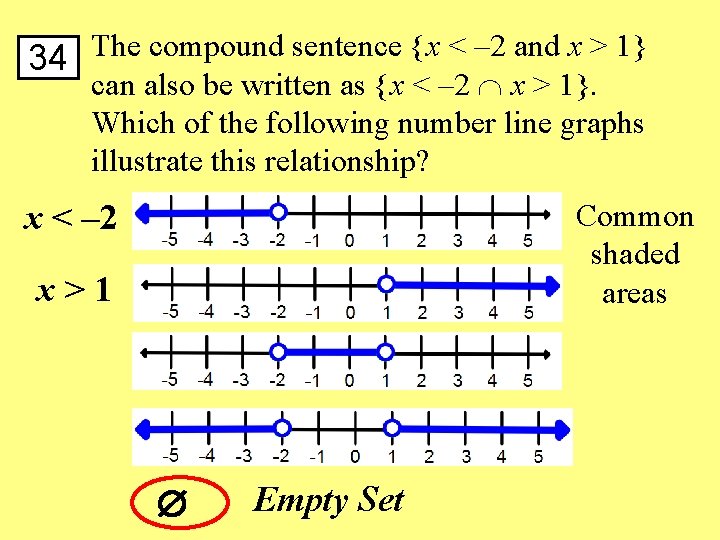
34 The compound sentence {x < – 2 and x > 1} can also be written as {x < – 2 x > 1}. Which of the following number line graphs illustrate this relationship? x < – 2 Common shaded areas x>1 Empty Set

35 Set A = {x > – 2} and set B = {x < 1}. Which of the following illustrates A B ? x > – 2 x<1 Answer Combine shaded areas