Unit 1 Matter Measurement Scientific Notation Accuracy Precision

Unit 1: Matter & Measurement Scientific Notation, Accuracy, Precision & Error

Measurement measurement: quantity with number _______ and a unit _____. 42. 5 g 1. 05 m. L 16 cm

Scientific Notation A number is expressed in scientific notation when it is in the form a x 10 n where a is between 1 and 10 and n is an integer

Write the width of the universe in scientific notation. 210, 000, 000, 000 miles Where is the decimal point now? After the last zero. Where would you put the decimal to make this number be between 1 and 10? Between the 2 and the 1

2. 10, 000, 000, 000. How many places did you move the decimal? 23 When the original number is more than 1, the exponent is positive. The answer in scientific notation is 2. 1 x 1023

Express 0. 000 0902 in scientific notation. Where would the decimal go to make the number be between 1 and 10? 9. 02 The decimal was moved how many places? 8 When the original number is less than 1, the exponent is negative. 9. 02 x 10 -8

Let’s Practice! 1) What is 28750. 9 in scientific notation? A. B. C. D. 2. 87509 x 10 -5 2. 87509 x 10 -4 2. 87509 x 105

2) Which of the following expressions has NOT been correctly changed to sci. not. ? A. 0. 00456 = 4. 56 10– 3 B. 0. 0000254 = 2. 54 10– 5 C. 8, 426, 000 = 8. 426 106 D. 45, 200 = 4. 52 103

3) Express 1. 8 x 10 -4 in decimal notation. 0. 00018 4) Express 4. 58 x 106 in decimal notation. 4, 580, 000 Complete questions 1 -20 on WS #1: Scientific Notation, Accuracy, Precision & Error

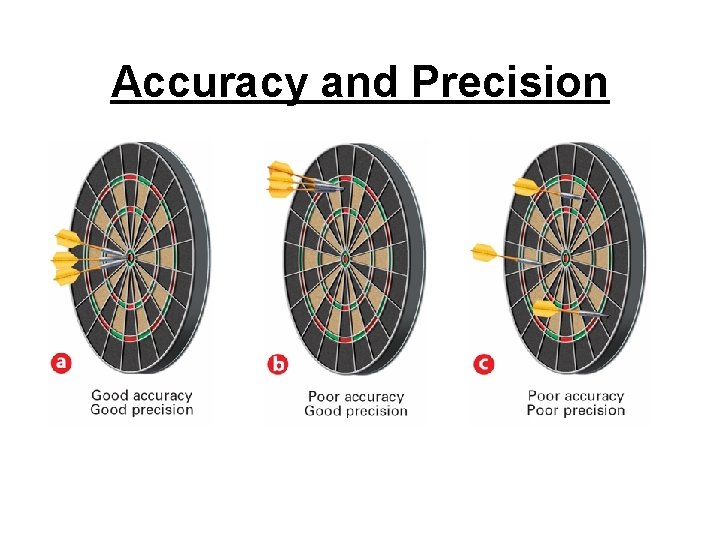
Accuracy and Precision and Error Accurate - measurement is close to the actual or true value of whatever is measured. Precise – (repeatable) measurements are close to one another. * precise if only the last digit varies

Accuracy and Precision

Practice Problems 1. Three students measure the volume of an object to be 10. 4 m. L, 10. 5 m. L, and 10. 7 m. L. The actual volume is 10. 6 m. L. a) Are the measurements accurate? Yes! b) Are the measurements precise? Yes!

2. Five students weigh a sample of metal. Here are their measurements: 2. 39 g, 2. 60 g, 2. 46 g, 2. 25 g, 2. 58 g The actual weight of the metal is 2. 60 g. a) Are the measurements accurate? No Calculate the average to find out. (2. 39 + 2. 60 + 2. 46 + 2. 25 + 2. 58) = 2. 46 g 5 b) Are the measurements precise? No

3. Which set of measurements of a 2. 00 -g object is the most precise? A. 2. 00 g, 2. 13 g, 1. 92 g B. 2. 10 g, 2. 00 g, 2. 20 g C. 2. 05 g, 2. 04 g, 2. 05 g D. 1. 50 g, 2. 00 g, 2. 50 g

Determining Error The actual (accepted) value is the correct value based on reliable references. The experimental value is the value measured in the lab. ( experimental value – actual value) X 100 % error = actual value Percent error tells you how accurate your results are.

% Error Example 1: Determine the % error if the measured temperature of a solution is 99. 1˚C and the actual temperature is 100. 0˚C % error = (99. 1˚C – 100. 0˚C) x 100. 0˚C = - 0. 9˚C x 100. 0˚C = - 0. 9%

% Error Example 2 A technician experimentally determined the boiling point of octane to be 127. 1˚C. The actual boiling point of octane is 125. 7˚C. Calculate the percent error. Percent error = (127. 1˚C – 125. 7˚C) x 100 125. 7˚C = 1. 4˚C x 100 125. 7˚C = 1. 11% Complete WS #1: Scientific Notation, Accuracy, Precision & Error