Unit 1 Lesson 1 Angles and their Measures

Unit 1, Lesson 1 Angles and their Measures

What is an angle? Two rays with the same Endpoint.

Make a table Term Definition Picture

Trigonometry vocabulary Initial side – start side of angle Terminal side – end side of angle Standard position – An angle whose initial side is on the positive x-axis Coterminal angle – Angles that have the same terminal side

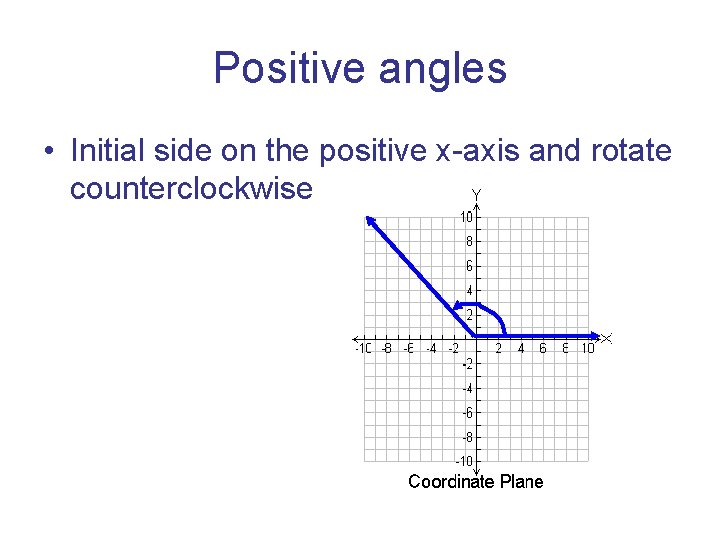
Positive angles • Initial side on the positive x-axis and rotate counterclockwise

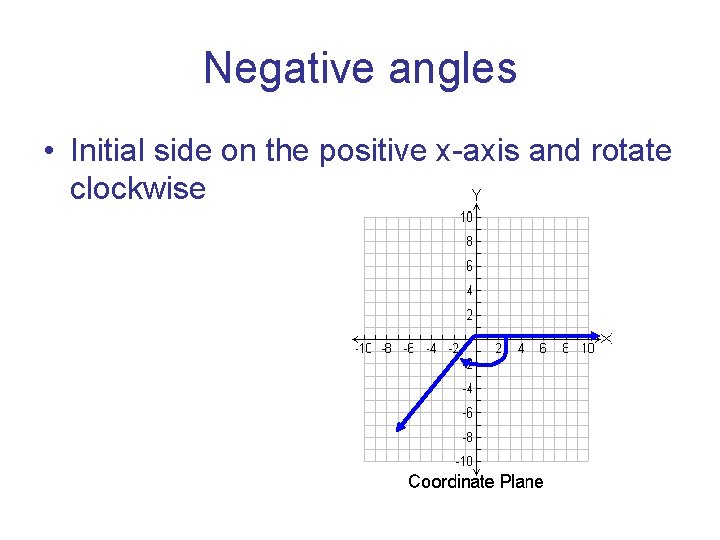
Negative angles • Initial side on the positive x-axis and rotate clockwise

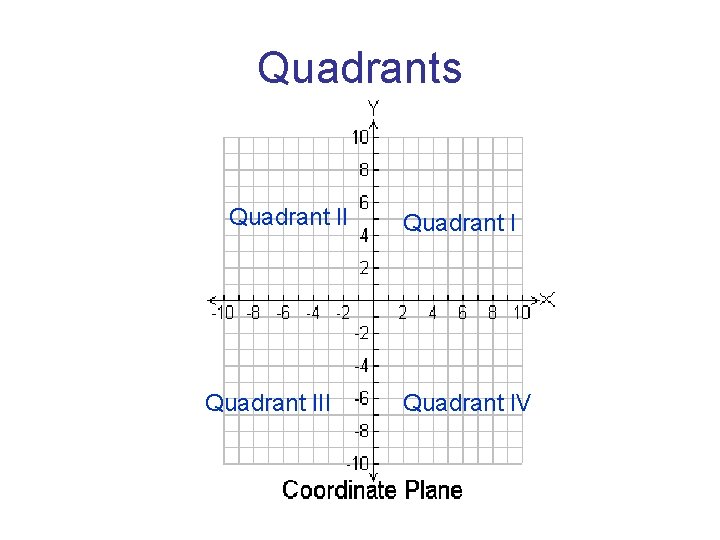
Quadrants Quadrant III Quadrant IV

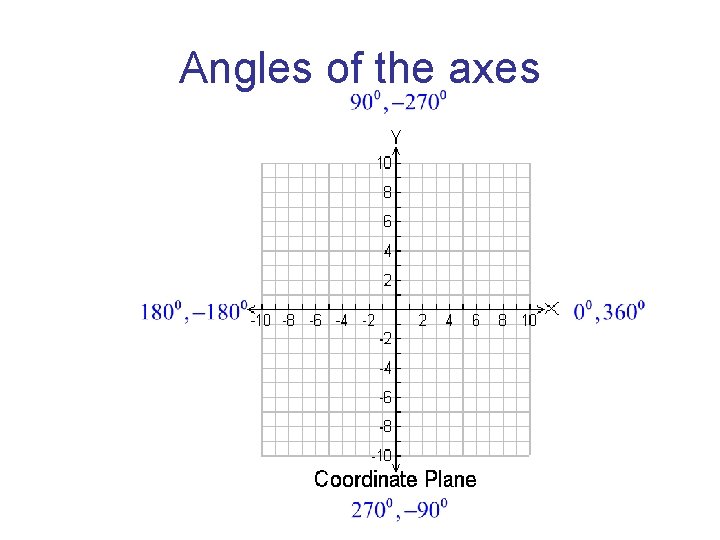
Angles of the axes

• Variables you will see for angle measures

Examples • What quadrant is the terminal side of the angle in? (Make a sketch of the angle)

Examples - Coterminal angles • You can add or subtract multiples of 360 or -360 to find coterminal angles • Find 2 coterminal angles (one positive and one negative) for 35 o • Find 2 coterminal angles (one positive and one negative) for -23 o • Find 2 coterminal angles (one positive and one negative) for 740 o

Decimal degree vs. degree/minute/second • Sometimes angles are not whole numbers • When this happens, they take 2 forms – Degree decimal - 76. 5 o – Degree/minute/second (DMS) 53 o 18’ 23” • To change from DMS to decimals, divide the minutes by 60 and the seconds by 3600 and add all together • To change from decimal to DMS, multiply decimal by 60 – this is the minutes, then multiply resulting decimal by 3600, this is the seconds

Examples - DMS • Convert to decimal • 35 o 18’ 27” • -142 o 54’ 32” • Convert to DMS • -23. 873 o • 740. 5 o

Radians

Examples • Change from degrees to radians • Change from radians to degrees

Coterminal Examples using radians • Add or subtract 2π to angle

Complementary/Supplementary • Complementary angles add up to 90 o or o • Supplementary angles add up to 180 or

Examples o • What angle is complementary to 36 ? o • What angle is supplementary to 36 ? • What angle is complementary to ? • What angle is supplementary to ?

Finding arc lengths • • S=rθ S is arc length r = radius θ = central angle, must be in radians

Examples • Find the length of the arc with radius 20 in and central angle of π/4 • Find the length of an arc with radius 5 m and central angle of 180 o • Find the measure of the central angle is arc length is 6 in and radius is 18 in