Unit 1 Introduction to Physics Book Chapter 1

Vocabulary • • Inference Hypothesis Independent Variable Dependent Variable Theory SI Unit Mass • • • Weight Accuracy Precision Significant Figure Scalar Vector

Physics • Physics is a study of the fundamental laws of nature • These fundamental laws can be expressed in terms of mathematical equations • Kinematics (motion), Energy, Momentum, Electricity, Magnetism, Thermodynamics, Waves and Particles

Scientific Method • • Observe Infer and hypothesize Test Conclude *Bubble Gum Lab

Units and Dimensions • Metric System (SI) • Base Unit – the standard “measuring stick” for a physical quantity • Length – meter (m) • Time – second (s) • Mass – kilogram (kg) • We use kilograms as the base unit for our formula calculations instead of grams

Converting between units using dimensional analysis • The metric system uses prefixes, which designate common multiples in powers of 10 to convert between larger and smaller units • Example: meters to centimeters, grams to kilograms, etc. • Use the prefix chart to help convert between different units within the metric system

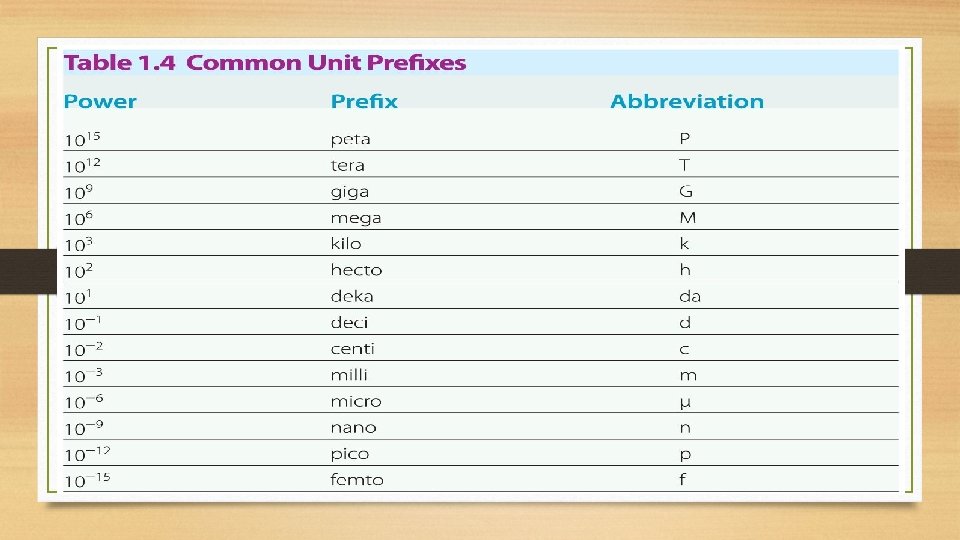
Unit conversion Equivalents • Use the Common Unit Prefixes chart to figure out the unit equivalents: • • 1 m = 1 x 103 mm 1 g = 1 x 10 -3 kg 1 L = 1 x 10 -2 c. L Note that the whole number 1 goes where the base unit (m, L, g, s, etc. ) is and the power (1 x 10? ) goes where the prefix (mm, kg, c. L, etc. ) is located

Conversion Fractions • Once you know your equivalent statement, use that information to make a conversion fraction • 1 m = 1 x 103 mm 1 m 1 x 103 mm or 1 x 103 mm 1 m *These fractions are conversion fractions, they are both correct statements that 1 meter is equal to 1 x 103 mm

$Dimensional Analysis (train tracks) • Once you know your conversion fractions, you can convert$

Dimensional Analysis (train tracks) • Once you know your conversion fractions, you can convert between the units using a method known as dimensional analysis • Step 1: Take your given information and write it down first as a fraction • So if your given is 10 meters, you would write down 10 meters to make it a fraction 1 • Step 2: Use conversion fractions to convert between the unit you are given and the unit you are trying to end up with, so that the units cancel out

Examples: • • 14 m = ? mm 4 kg = ? g 18 cs = ? s 3 kg = ? mg 9 ML = ? d. L 5 x 10 -6 m = ? km 3. 2 x 1015 ms = ? Ks

Conversions with non-metric units • 2 years = ? seconds • 316 ft = ? meters • 1 m = 3. 281 ft • 55 mi/h = ? m/s • 1 mile = 5, 280 feet • 3. 5 m/s = ? km/h *For extra practice problems: Book page 22 #20 -21; page 38 #49, 50, 53 Lab Activity

Basic Math for Physics • Any equation can be rearranged to give information about any of the physical quantities in it • Ex: If I know how fast I am going (my speed) and I know how far I have to go (distance), I can use the speed equation which says that S = d / t to calculate how long it will take for me to reach my destination (time) • Even though the speed equation is written on the formula chart to solve for speed, it can be rearranged to solve for distance or time

Rearranging Equations Practice • D=M Solve for M, solve for V V • S=d Solve for d, solve for t t • F = ma • KE = ½ mv 2 Solve for m, solve for a Solve for m, solve for v

Accuracy and Precision • Accuracy is a measure of how close a measured value of a quantity is to its actual value • Precision is a measure of how close together the values of a series of measurements are to one another • Lab

Significant Figures • What are they? ? ? • Significant figures indicate accuracy • It is the number of digits that are actually measured (what you can actually see on your measuring instrument) plus one estimated digit • The more decimal places a number has, the more accurate the instrument making the measurements

Rules for Significant Figures • Non-zero numbers are always significant • 66 has two significant figures • 879, 548 has six significant figures • Rules for Zeros: • If it is between two non-zero numbers it is always significant. Ex: 808 has three • If it is after a non-zero number and after a decimal it is significant. Ex: 8. 0 has two • If it is after a decimal but before a non-zero number (leading zero) it is not significant. Ex: 0. 005 only has one Ex: 0. 6 only has one Ex: 0. 0200 has three • If a number is written in scientific notation, all the numbers that are written (before the x 10? ) are significant

Examples: • How many significant figures are in the following numbers? • • • 8, 900. 0 2. 0 508, 000 4. 50 x 107

Calculations using significant figures • Addition/Subtraction • You round your answer so that the number of decimal places in your answer is equal to the smallest number of decimal places in any of the input values • Ex: 15. 2 + 10 + 4. 25 = ? Ex: 24. 386 – 7. 6942 = ? • Multiplication/Division • You round your answer so that the answer has the same overall number of significant figures and the smallest overall number of significant figures in any of the input values • Ex: 10 x 10 = ? Ex: 10. 0 x 10. 0 = ? Ex: 15 x 3 = ? • For extra practice problems: Book page 32 #31 -32, 35 -38 • Activity