Unit 1 Introduction to Chemistry Part 2 Scientific

Unit 1 – Introduction to Chemistry Part 2: Scientific Measurement

Uncertainty in Measurement n The # associated with a measurement is obtained using a measuring device • Last digit has to • Estimated digits n n be estimated are “uncertain” A measurement always has some degree of uncertainty. Communicating our uncertainty in a measurement is equally important as the measurement itself!

Uncertainty in Measurement

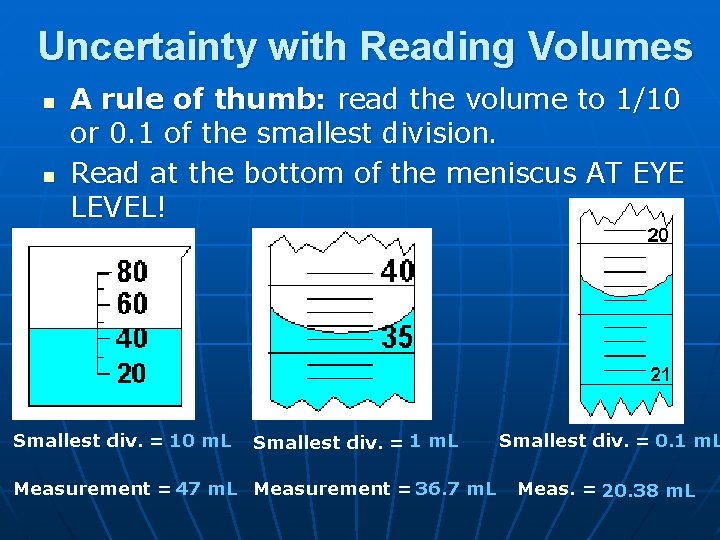
Uncertainty with Reading Volumes n n A rule of thumb: read the volume to 1/10 or 0. 1 of the smallest division. Read at the bottom of the meniscus AT EYE LEVEL! Smallest div. = 10 m. L Smallest div. = 1 m. L Measurement = 47 m. L Measurement = 36. 7 m. L Smallest div. = 0. 1 m. L Meas. = 20. 38 m. L

You Try It! What is the length of the wooden stick? 1) 4. 5 cm 2) 4. 54 cm 3) 4. 547 cm

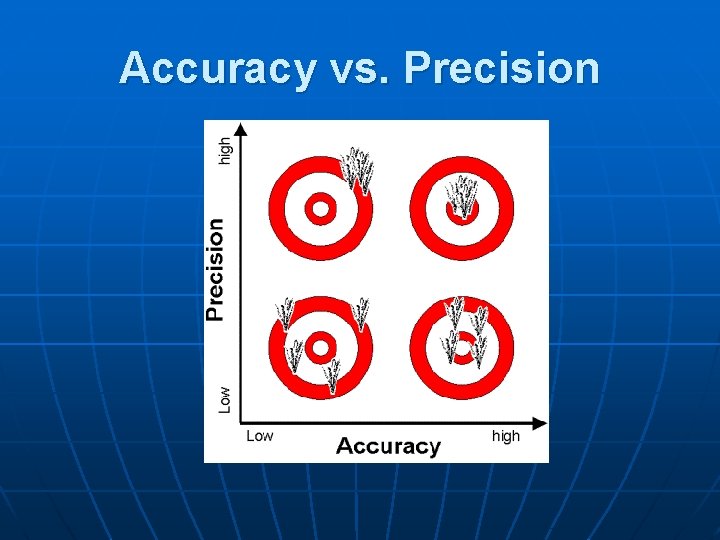
Accuracy vs. Precision n n Accuracy - how close a measurement is to the accepted value Precision - how close a series of measurements are to each other ACCURATE = CORRECT PRECISE = CONSISTENT

Accuracy vs. Precision

Error n Definition = The difference between an accepted value and an experimental value • Accepted- what you are “supposed” to get • Experimental- what you “actually” get n Take the absolute value No negative values n |experimental – accepted| = error n

Percent Error n n Indicates accuracy of a measurement Ratio of an error to an accepted value your value

Percent Error Example n A student determines the density of a substance to be 1. 40 g/m. L. Find the % error if the accepted value of the density is 1. 36 g/m. L. % error = 3%

Significant Figures n n Indicate precision (uncertainty) of a measurement. Recording Sig Figs • Sig figs in a measurement include the known digits plus a final estimated digit n The more digits reported, the more precise the measurement 2. 35 cm

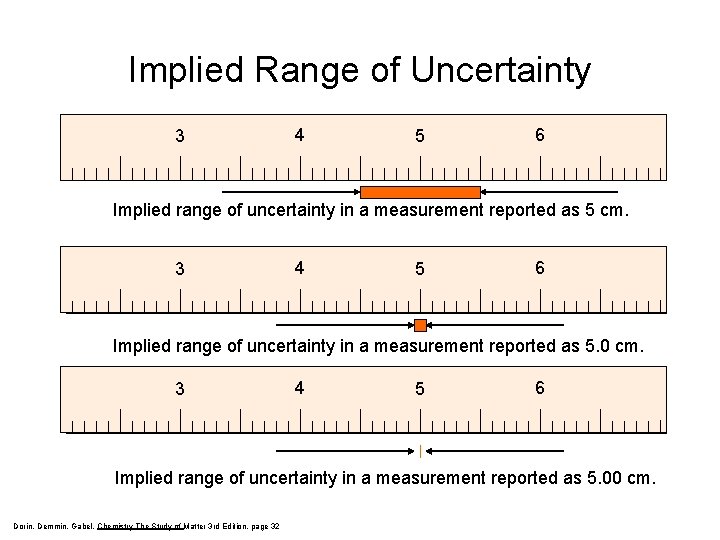
Implied Range of Uncertainty 3 4 5 6 Implied range of uncertainty in a measurement reported as 5 cm. 3 4 5 6 Implied range of uncertainty in a measurement reported as 5. 00 cm. Dorin, Demmin, Gabel, Chemistry The Study of Matter 3 rd Edition, page 32

Significant Figures n Counting Sig Figs • Count all numbers EXCEPT: Leading zeros -- 0. 0025 n Trailing zeros without a decimal point -2, 500 n

Atlantic Pacific Rule n n n If a decimal point is Present, start counting from the Pacific (left) side at the 1 st non-zero number. If the decimal point is Absent, start counting from the Atlantic (right) side at the 1 st non-zero number. Count until you run out of numbers!

Significant Figures Practice Counting Sig Figs Practice Problems 1. 23. 50 cm 4 sig figs 2. 402 g 3 sig figs 3. 5, 280 g 3 sig figs 4. 0. 080 L 2 sig figs

Significant Figures n Calculating with Sig Figs • Multiplication/Division n The measurement with the fewest sig figs determines the # of sig figs in the answer. (13. 91 g/cm 3)(23. 3 cm 3) = 324. 103 g 4 SF 324 g

Significant Figures n Calculating with Sig Figs (cont. ) • Addition/Subtraction n The measurement with the fewest decimal places determines how many decimal places can be in the answer. 3. 75 m. L + 4. 1 m. L 7. 85 m. L 7. 9 m. L 224 g + 130 g 354 g 350 g

Significant Figures n Calculating with Sig Figs (cont. ) • Exact Numbers do not limit the # of sig figs in the answer. n Counting numbers: 12 students n Exact conversions: 1 m = 100 cm n “ 1” in any unit conversion: 1 in = 2. 54 cm

Significant Figures Practice Calculating with Sig Figs Practice Problems 1. (15. 30 g) ÷ (6. 4 m. L) 4 SF 2 SF = 2. 390625 g/m. L 2. 4 g/m. L 2 SF 2. 18. 9 g - 0. 84 g 18. 06 g 18. 1 g 1 DECIMAL PLACE

PRACTICE! n Accuracy, Precision & Sig Figs WS

Scientific Notation n n Way of expressing really big numbers or really small numbers How to write scientific notation • Product of 2 factors n a number with only one digit in front of the decimal n power of 10 # x 10 x

Scientific Notation 65, 000 kg 6. 5 × 10 ? 4 kg n Converting into Sci. Notation: • Move decimal until there’s 1 digit to its left. Places moved = exponent. • Large # (>1) positive exponent Small # (<1) negative exponent • Only include sig figs!

PRACTICE: Change to scientific notation. 12, 340 = 0. 369 = 0. 008 = 1, 000, 000 = 1. 234 x 104 3. 69 x 10– 1 8 x 10– 3 1 x 109

Scientific Notation 5. 4 x 10 -3 kg 0. 0054 ? kg n Converting out of Sci. Notation: • Simply move the decimal point to the right for positive exponent of 10. • Move the decimal point to the left for negative exponent of 10. • Use zeros for placeholders.

PRACTICE: Change to standard notation. 1. 87 x 10– 5 = 0. 0000187 3. 7 x 108 = 370, 000 7. 88 x 101 = 78. 8 2. 164 x 10– 2 = 0. 02164

Converting into and out of Scientific Notation Practice 1. 2, 400, 000 cg 2. 4 106 cg 2. 0. 00256 kg 2. 56 10 -3 kg 3. 7 10 -5 km 0. 00007 km 4. 6. 2 104 mm 62, 000 mm

Rule for Multiplication Calculating with Numbers Written in Scientific Notation When multiplying numbers in scientific notation, multiply the first factors and add the exponents. Sample Problem: Multiply 3. 2 x 10 -7 by 2. 1 x 105 (3. 2) x (2. 1) = 6. 7 (-7) + (5) = -2 or 10 -2 Exercise: 1. 46 x 108 x 1. 5 x 104 6. 7 x 10 -2 2. 2 x 1012

Rule for Division Calculating with Numbers Written in Scientific Notation When dividing numbers in scientific notation, divide the first factor in the numerator by the first factor in the denominator. Then subtract the exponent in the denominator from the exponent in the numerator. Sample Problem: Divide 6. 4 x 106 by 1. 7 x 102 (6. 4) (1. 7) = 3. 8 x 104 (6) - (2) = 4 or 104 Exercise: 2. 4 x 10 -7 3. 1 x 1014 7. 7 x 10 -22

Rule for Addition and Subtraction Calculating with Numbers Written in Scientific Notation In order to add or subtract numbers written in scientific notation, you must express them with the same power of 10. Sample Problem: Add 5. 8 x 103 and 2. 16 x 104 (5. 8 x 103) + (21. 6 x 103) = 27. 4 x 103 2. 74 x 104 Exercise: 8. 32 x 10 -7 + 1. 2 x 10 -5 1. 3 x 10 -5

Calculating with Scientific Notation Practice = -65. 25 x 10 -10 report -6. 5 x 10 -9 (2 sig. figs. ) = 5. 3505 x 103 report 5. 35 x 103 (3 sig. figs. ) = 0. 5842 x 10 -12 report 5. 84 x 10 -13 (3 sig. figs. ) 0. 88 x 1012 = 4. 18 x 1012 report 4. 2 x 1012 (1 dec. place) 0. 435 x 10 -8 = 4. 665 x 10 -8 report 4. 7 x 10 -8 (1 dec. place)

Using the Exponent Key on a Calculator for Scientific Notation EE EXP

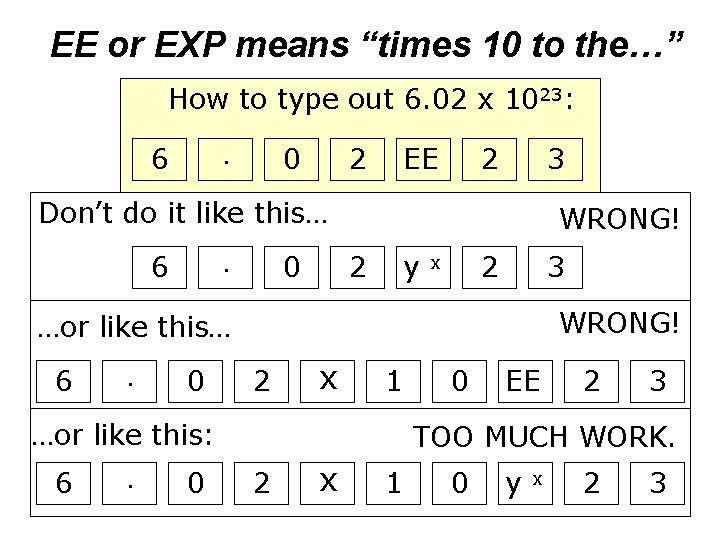
EE or EXP means “times 10 to the…” How to type out 6. 02 x 1023: 6 0 . 2 EE 2 3 Don’t do it like this… 6 0 . WRONG! 2 y 2 x 3 WRONG! …or like this… 6 . 0 2 x 1 …or like this: 6 . 0 0 EE 2 3 TOO MUCH WORK. 2 x 1 0 y x 2 3

Scientific Notation Calculator Practice n Solve the following problem using your calculator. (5. 44 × 107 g) ÷ (8. 1 × 104 mol) = Type on your calculator: 5. 44 EXP EE 7 ÷ 8. 1 EXP EE 4 EXE ENTER 2 g/mol 6. 7 × 10 = 670 g/mol = = 671. 6049383

Units of Measurement n Quantity = number + unit UNITS MATTER!!

SI Units of Measurement Quantity Symb ol l Length Unit meter Abbre v. m Mass m kilogram kg Time t second s Temp T Kelvin K Amount n mole mol

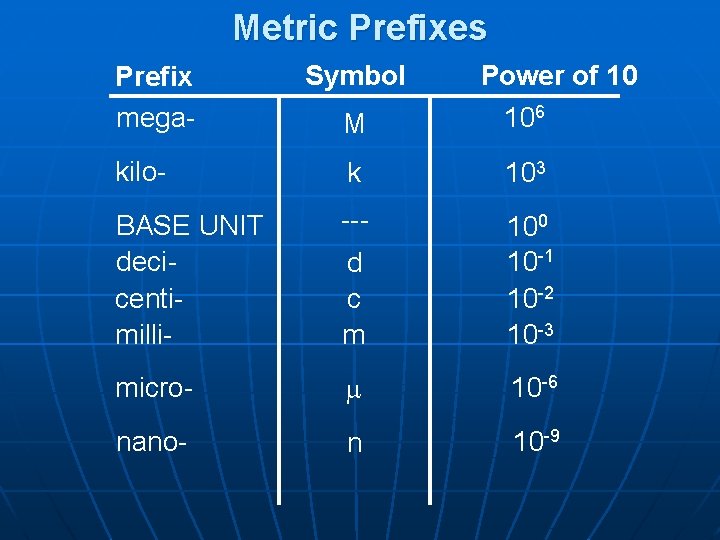
Metric Prefixes Prefix mega- Symbol M Power of 10 106 kilo- k 103 BASE UNIT decicentimilli- --d c m 100 10 -1 10 -2 10 -3 micro- 10 -6 nano- n 10 -9

1024 g 1021 g 1018 g Earth’s atmosphere to 2500 km 1015 g 1012 g Giga- 109 g Mega- 106 g Kilo- 103 g base 100 g milli- 10 -3 g micro- 10 -6 g nano- 10 -9 g pico- 10 -12 g femto- 10 -15 g atomo- 10 -18 g 10 -21 g 10 -24 g Kelter, Carr, Scott, Chemistry A Wolrd of Choices 1999, page 25 Ocean liner Indian elephant Average human 1. 0 liter of water Grain of table salt Typical protein Uranium atom Water molecule

Metric Conversions 1. Find the difference between the exponents of the two prefixes. 2. Move the decimal that many places. To the left or right?

Metric Conversions

Metric Conversions 532 m = NUMBER = UNIT 0. 532 km ______ NUMBER UNIT

Metric Conversions Practice 1. 0. 2 20 cm = ____ m 2. 0. 032 L = 3. 0. 805 80, 500 cm = ____ km 32 ____ m. L

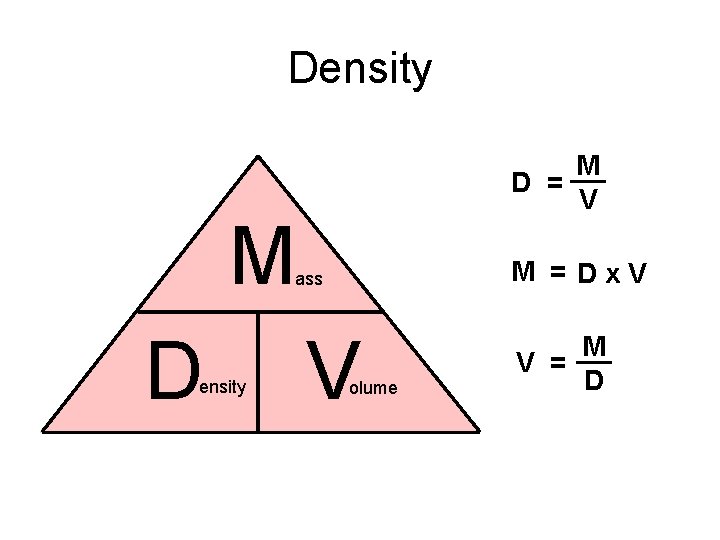
Density n How much mass takes up a certain amount of volume D= n M V The density of a substance will NOT change • If the mass changes, then the volume will change also • So, what kind of property is density?

Density M D = V M M = Dx. V ass D ensity V olume M V = D

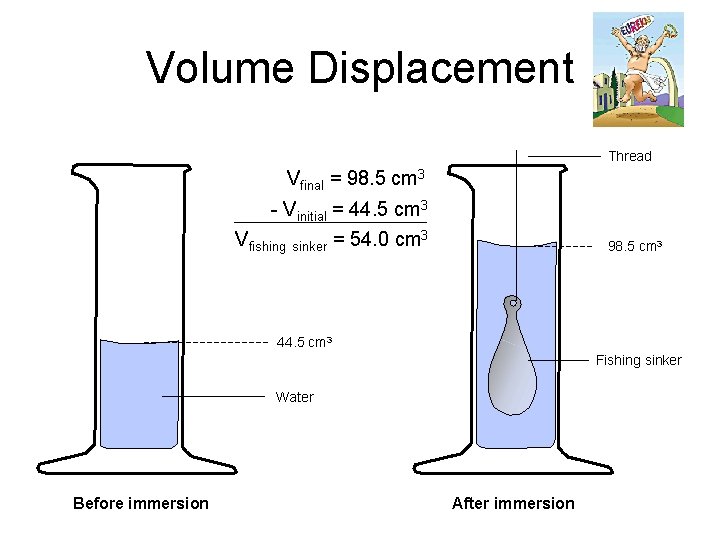
Density via Volume Displacement n To find the volume of irregularly shaped objects, we must use Archimedes’ principle. • an object, when placed in a liquid, will displace a volume of liquid equal to its own volume

Volume Displacement Thread Vfinal = 98. 5 cm 3 - Vinitial = 44. 5 cm 3 Vfishing sinker = 54. 0 cm 3 98. 5 cm 3 44. 5 cm 3 Fishing sinker Water Before immersion After immersion

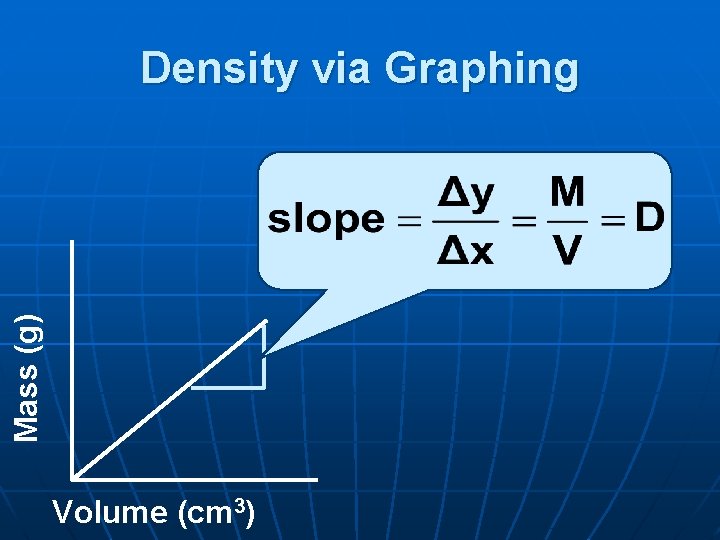
Mass (g) Density via Graphing Volume (cm 3)

Common Units of Density n grams/ cm 3 n grams/ m. L Important Conversion to Know: 1 m. L = 1 cm 3

Density Practice Problem #1 n An object has a volume of 825 cm 3 and a density of 13. 6 g/cm 3. Find its mass. GIVEN: WORK: V = 825 cm 3 D = 13. 6 g/cm 3 M=? M = DV M = (13. 6 g/cm 3)(825 cm 3) M = 11, 200 g How many kg is this? ? ?

Density Practice Problem #2 n A liquid has a density of 0. 87 g/m. L. What volume is occupied by 25 g of the liquid? GIVEN: WORK: D = 0. 87 g/m. L V=? M = 25 g V=M D V= 25 g 0. 87 g/m. L V = 29 m. L