UNIT 1 GEOMETRY REVIEW POWERPOINT Each slide has

UNIT 1: GEOMETRY REVIEW POWERPOINT • Each slide has a practice problem from Unit 1: Geometry. • Please solve the problem on your own, and then click through to see the correct answer.

Unit 1 Geometry Review

Unit 1 Geometry Review

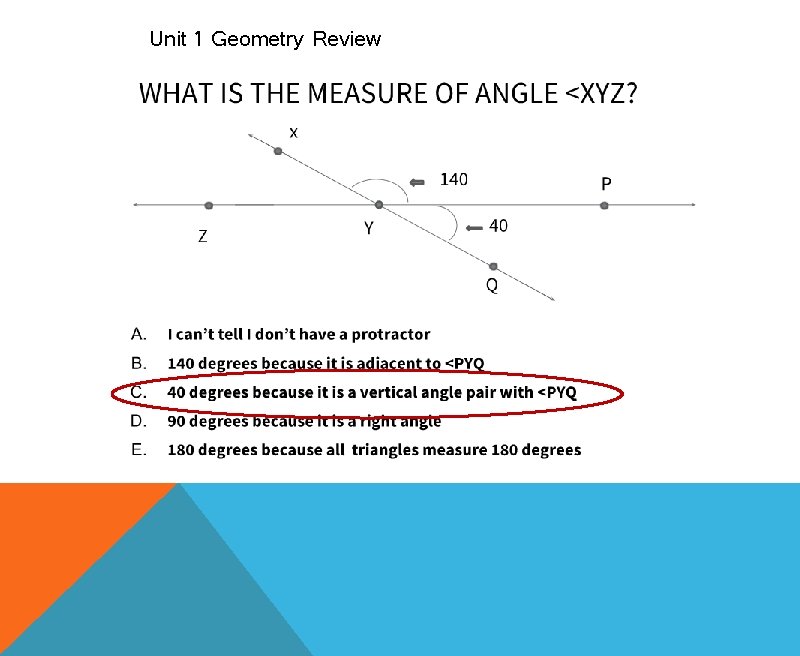
Unit 1 Geometry Review

Unit 1 Geometry Review

Unit 1 Geometry Review

Unit 1 Geometry Review

Unit 1 Geometry Review

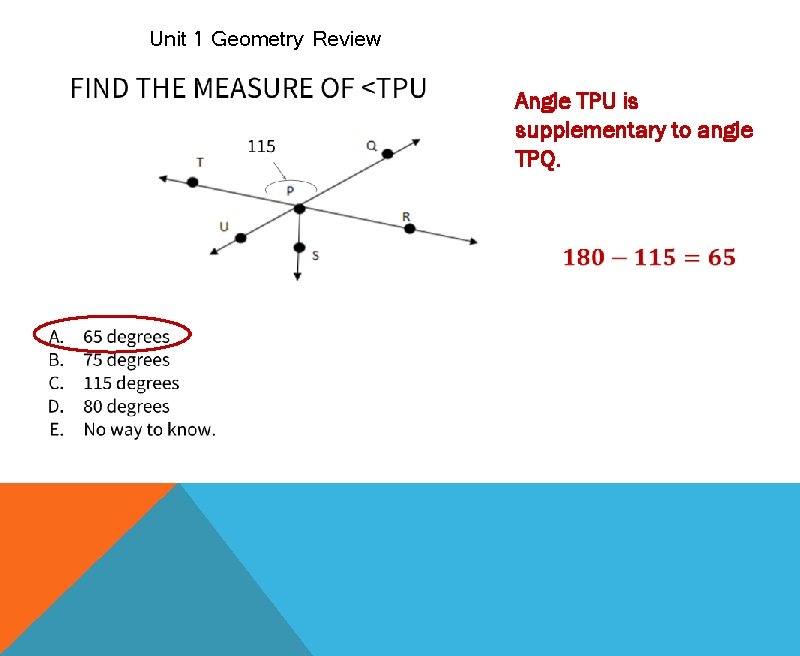
Unit 1 Geometry Review Angle TPU is supplementary to angle TPQ.

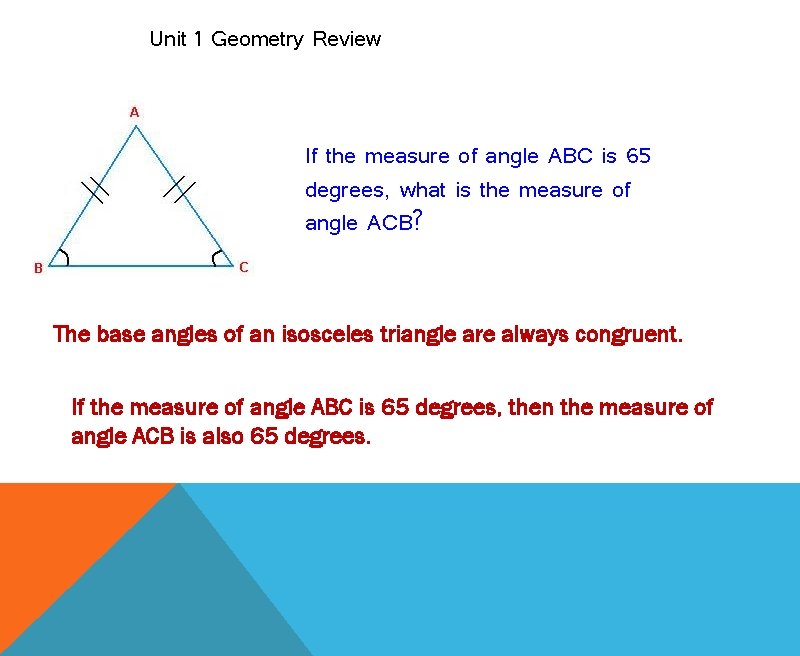
Unit 1 Geometry Review If the measure of angle ABC is 65 degrees, what is the measure of angle ACB? The base angles of an isosceles triangle are always congruent. If the measure of angle ABC is 65 degrees, then the measure of angle ACB is also 65 degrees.

Unit 1 Geometry Review The intersection of roads C and D creates a 53. 6 degree angle. What are the complementary and supplementary angles of this intersection? Complementary: 90 – 53. 6 = 36. 4 degrees Supplementary: 180 – 53. 6 = 126. 4 degrees

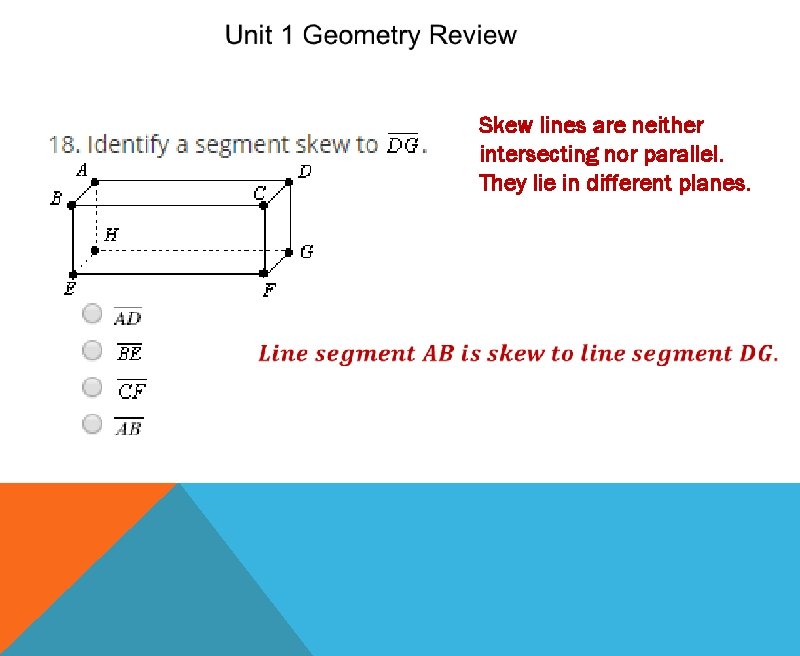
Skew lines are neither intersecting nor parallel. They lie in different planes.

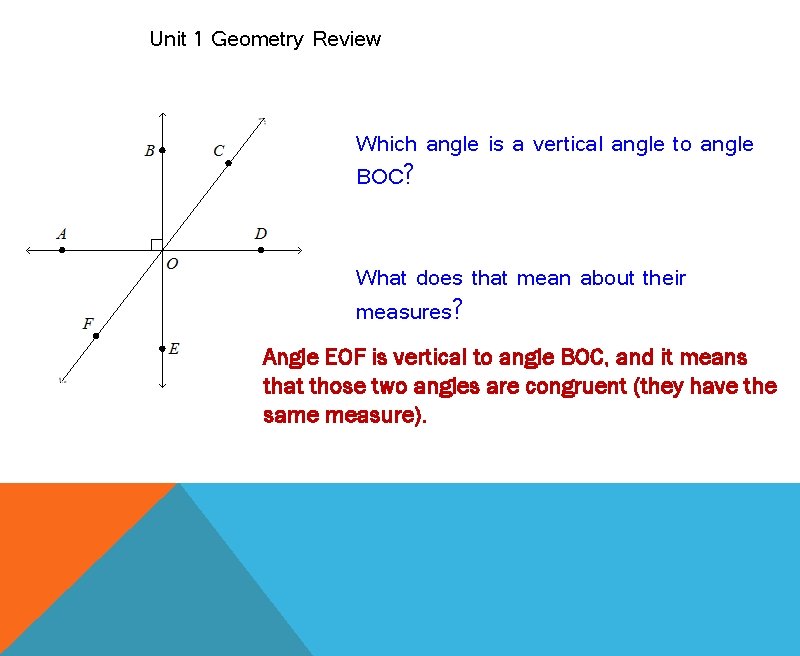
Unit 1 Geometry Review Which angle is a vertical angle to angle BOC? What does that mean about their measures? Angle EOF is vertical to angle BOC, and it means that those two angles are congruent (they have the same measure).

Unit 1 Geometry Review Point B is the midpoint of line segment AC. AB = 34 inches; A BC = ? B C Since B is the midpoint, AB and BC are the same length. BC = 34 inches

Unit 1 Geometry Review Line segment AB bisects line segment CD at point X. Where is the midpoint of line segment CD? The midpoint of line segment CD is at point x because a bisector divides a line segment into two congruent parts.

Unit 1 Geometry Review Name the quadrilateral that has one pair of opposite sides which are parallel. The quadrilateral that has exactly one pair of opposite sides which are parallel is a trapezoid.

Unit 1 Geometry Review Which of the following choices could be the side lengths of a triangle? 3, 6, 2 5, 4, 12 3, 10, 8 2, 8, 5 Choice 3: 10 -3=7 3+10=13 The third side must be greater than 7 and less than 13. 8 is greater than 7 and less than 13.

Unit 1 Geometry Review The angles in a triangle are 36 degrees, 52 degrees, and 92 degrees. Classify the triangle by its angle measures. Because one of the angles is greater than 90 degrees, the triangle is an obtuse triangle.

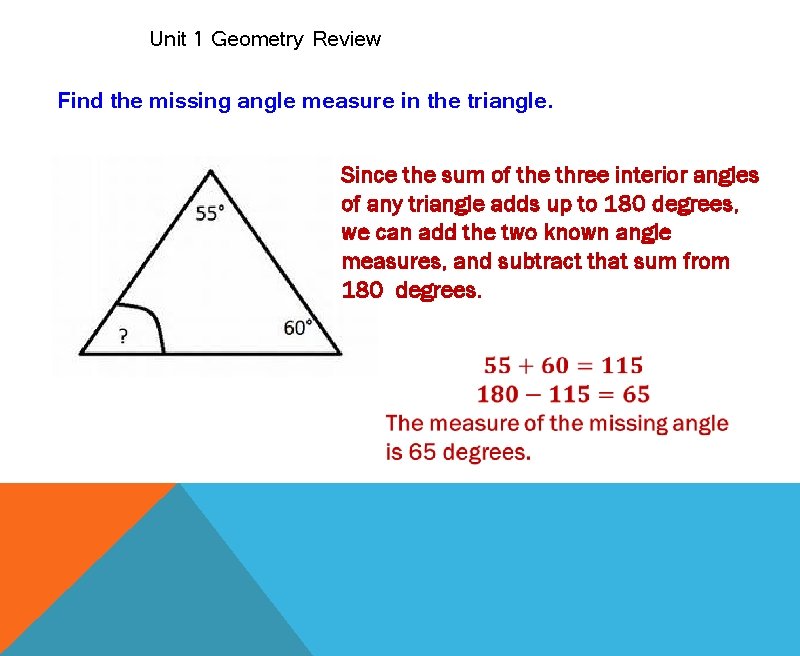
Unit 1 Geometry Review Find the missing angle measure in the triangle. Since the sum of the three interior angles of any triangle adds up to 180 degrees, we can add the two known angle measures, and subtract that sum from 180 degrees.

Unit 1 Geometry Review Identify the polygon and identify it as regular or irregular. The polygon has six sides, so it is a hexagon. Since the side lengths are not all the same length and the angles do not have the same measures, that makes the polygon an irregular polygon. The polygon is an irregular hexagon.

Unit 1 Geometry Review Classify the polygon. This quadrilateral has 4 sides, and exactly one pair of opposite, parallel sides. That makes the polygon a trapezoid.

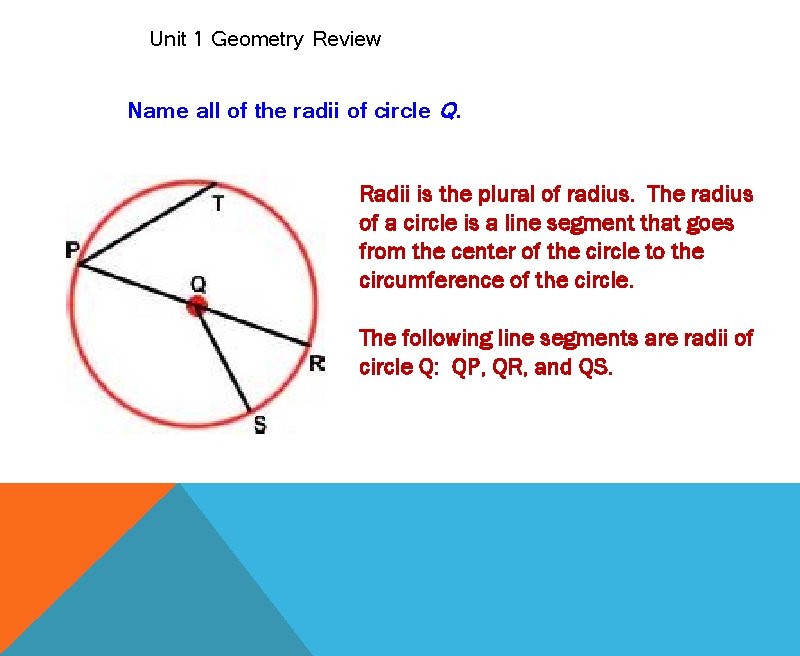
Unit 1 Geometry Review Name all of the radii of circle Q. Radii is the plural of radius. The radius of a circle is a line segment that goes from the center of the circle to the circumference of the circle. The following line segments are radii of circle Q: QP, QR, and QS.

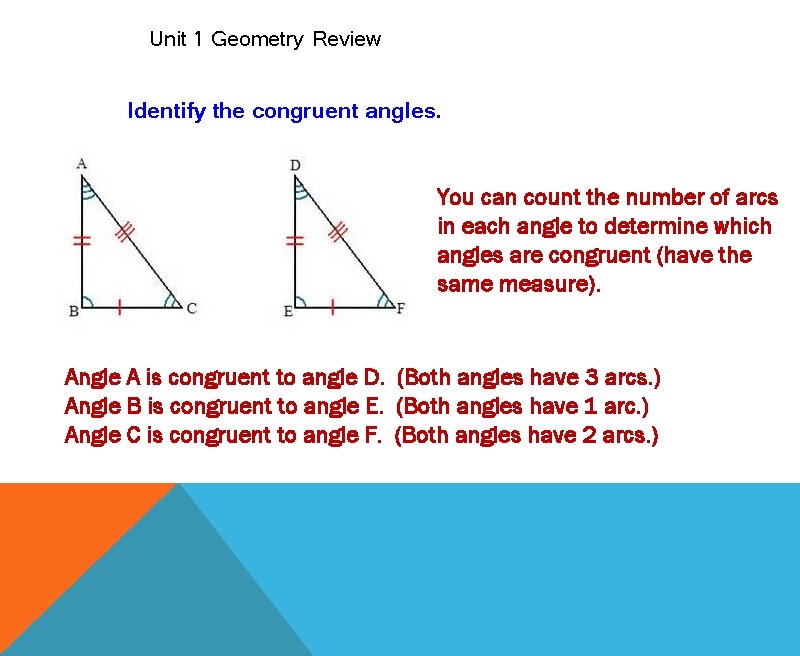
Unit 1 Geometry Review Identify the congruent angles. You can count the number of arcs in each angle to determine which angles are congruent (have the same measure). Angle A is congruent to angle D. (Both angles have 3 arcs. ) Angle B is congruent to angle E. (Both angles have 1 arc. ) Angle C is congruent to angle F. (Both angles have 2 arcs. )

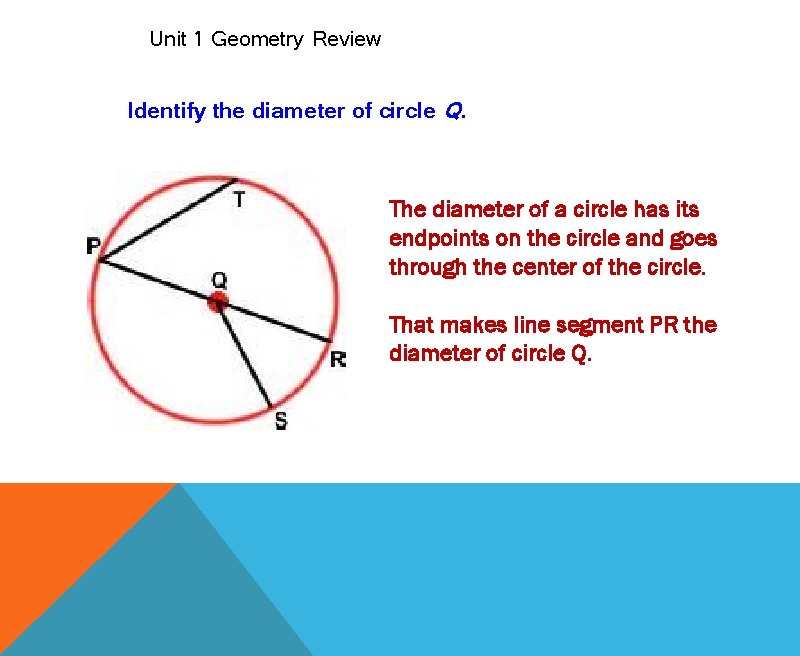
Unit 1 Geometry Review Identify the diameter of circle Q. The diameter of a circle has its endpoints on the circle and goes through the center of the circle. That makes line segment PR the diameter of circle Q.

Unit 1 Geometry Review Identify the angle as right, acute, straight, or obtuse. The measure of the angle is greater than 90 degrees and less than 180 degrees. That makes the angle an obtuse angle.

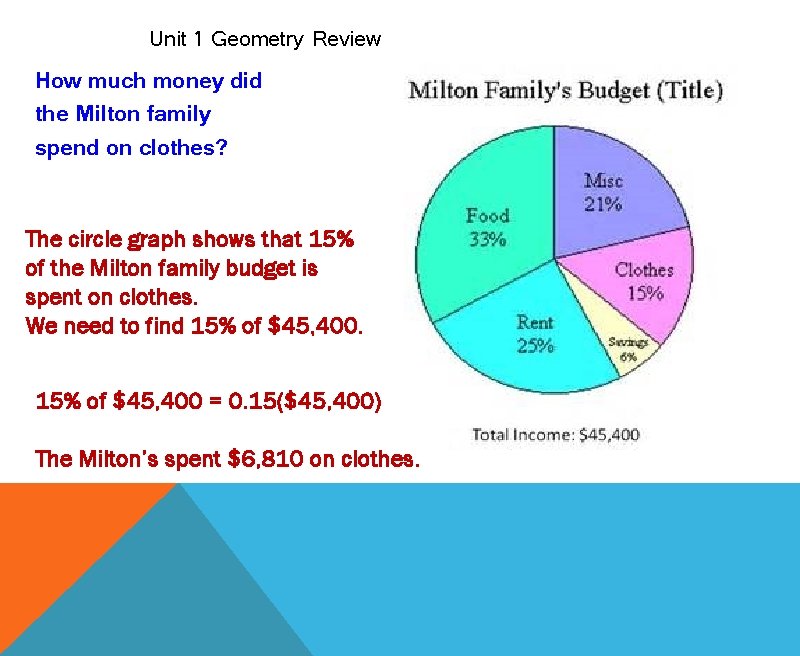
Unit 1 Geometry Review How much money did the Milton family spend on clothes? The circle graph shows that 15% of the Milton family budget is spent on clothes. We need to find 15% of $45, 400 = 0. 15($45, 400) The Milton’s spent $6, 810 on clothes.

Unit 1 Geometry Review If the measure of angle 2 is 50 degrees, what is the measure of angle 4? Angle 2 and angle 4 are vertical angles, so they are congruent (they have the same measure). The measure of angle 4 is 50 degrees.

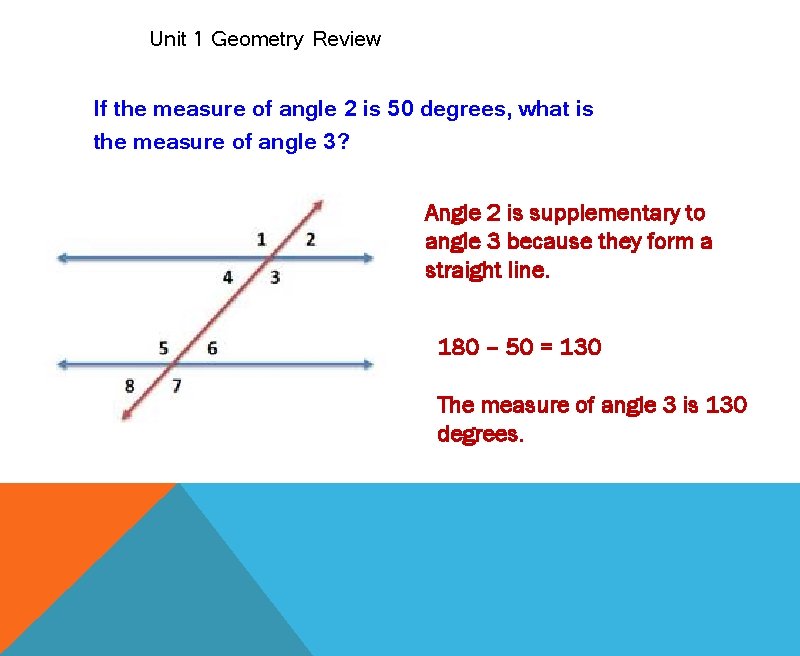
Unit 1 Geometry Review If the measure of angle 2 is 50 degrees, what is the measure of angle 3? Angle 2 is supplementary to angle 3 because they form a straight line. 180 – 50 = 130 The measure of angle 3 is 130 degrees.

Unit 1 Geometry Review The two living rooms shown below are congruent. The architect did not finish the diagrams. Find the missing side lengths and angle measures.

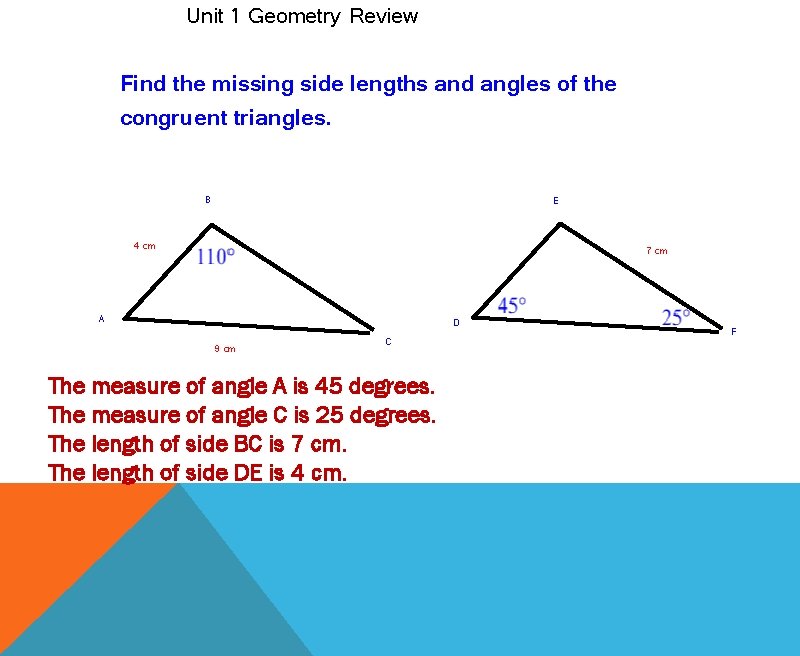
Unit 1 Geometry Review Find the missing side lengths and angles of the congruent triangles. B E 4 cm 7 cm A 9 cm C The measure of angle A is 45 degrees. The measure of angle C is 25 degrees. The length of side BC is 7 cm. The length of side DE is 4 cm. D F

Since ray SQ bisects angle RST, the two angles formed by that ray are congruent (they have the same measure). The measure of angle RSQ is 29 degrees because it is exactly half of the measure of angle RST. Half of 58 degrees is 29 degrees.

An angle bisector divides an angle into two congruent angles. Half of 34 degrees is 17 degrees, so the measure of angle ABD is 17 degrees.

The polygon has 5 sides, so it is a pentagon. The sides are not all the same length, so the polygon is an irregular pentagon.

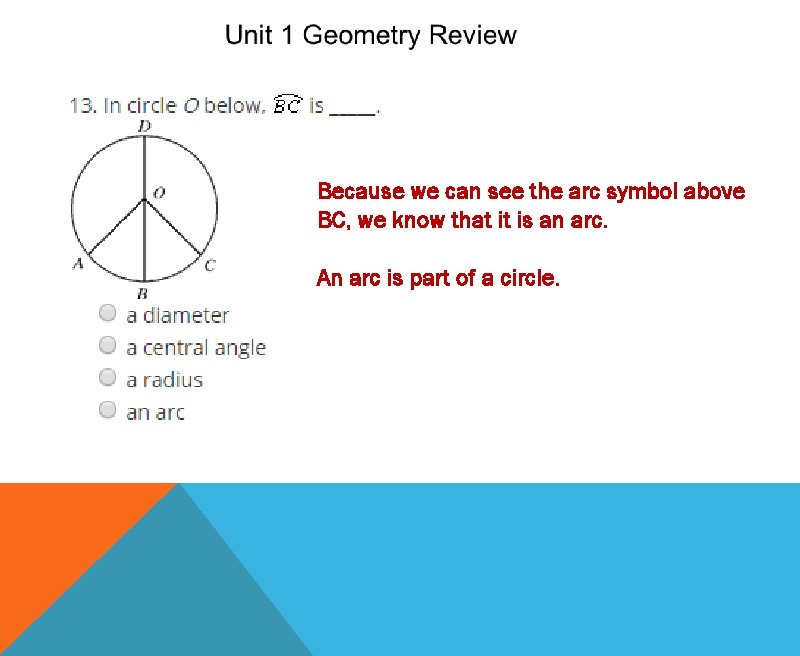
Because we can see the arc symbol above BC, we know that it is an arc. An arc is part of a circle.

The measure of angle RSQ is 29 degrees, and that is half the measure of angle RST. The measure of angle RST is 58 degrees. 2 times 29 is 58.

Since we know the measures of 2 of the interior angles on the left triangle, we can find the measure of angle x. 32 + 60 = 92 180 – 92 = 88 The measure of angle X is 88 degrees. Angle X and angle Y are supplementary. 180 – 88 = 92 The measure of angle Y is 92 degrees. Now we know the measures of 2 of the interior angles of the right triangle. 92 + 25 = 117 180 – 117 = 63 The measure of angle Z is 63 degrees,

SBAC Style Geometry Items Angle A has the least measure because it is directly across from the shortest side.

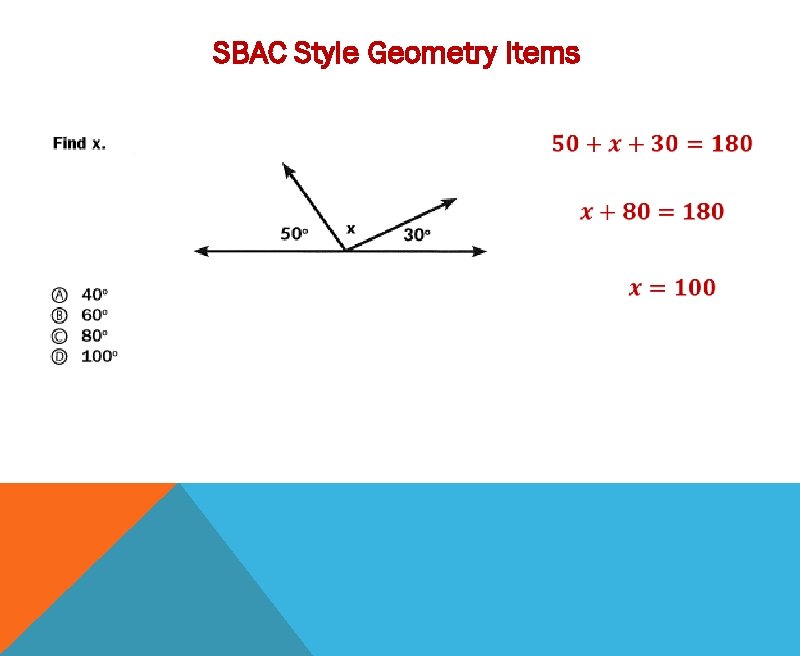
SBAC Style Geometry Items

SBAC Style Geometry Items

SBAC Style Geometry Items

SBAC Style Geometry Items Angle b and angle c are supplementary.

SBAC Style Geometry Items Supplementary angles have measures that add up to 180 degrees. If they have the same measure, they must each be 90 degrees.

SBAC Style Geometry Items Angle a and angle b are vertical angles, so they have the same measure. Angle a and angle c are supplementary.

SBAC Style Geometry Items