Unit 1 Functions and Models Part 6 Quadratic

Unit 1: Functions and Models Part 6: Quadratic Models

Quadratic Models A quadratic function is a function written in the form f(x)=ax 2+bx+c, where a≠ 0. The graph of a quadratic function is a parabola. If a>0, the quadratic’s vertex is a minimum, and it opens up. If a<0, the quadratic’s vertex is a maximum, and it opens down. The existence of these extrema makes quadratics different from linear and exponential functions.

Properties of Quadratics

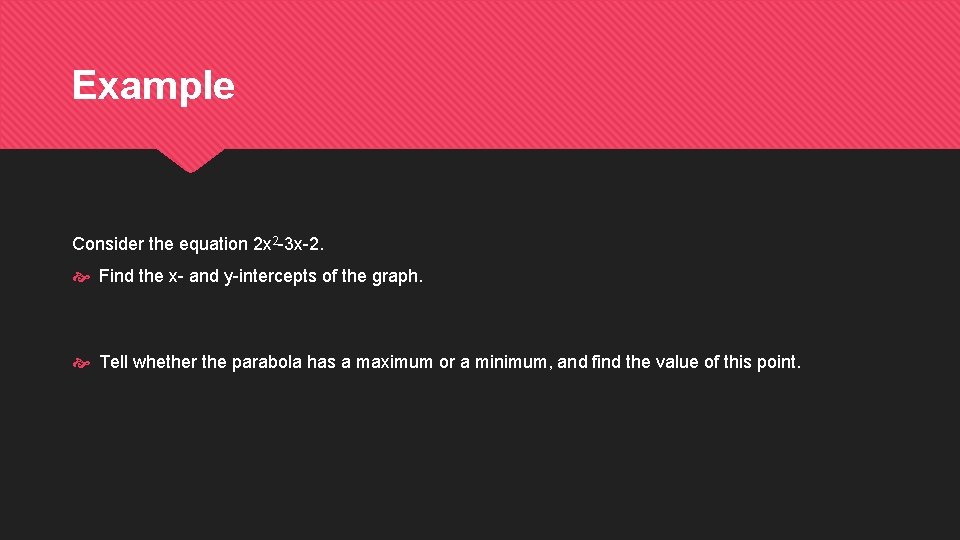
Example Consider the equation 2 x 2 -3 x-2. Find the x- and y-intercepts of the graph. Tell whether the parabola has a maximum or a minimum, and find the value of this point.

Using Known Quadratic Values

Example A ball is thrown from a height of 15 m with an initial velocity of 20 m/s. Find the relation between height (h) and time (t) after the ball is released. What is the height of the ball after 3 seconds? When will the ball hit the ground?

Finding a Quadratic Model (Through Three Points) To determine a unique quadratic model, you need a minimum of three non-collinear points. One way to fit a quadratic model is to identify specific points on the model and set up a system of equations. The model must allow for you to solve for a, b, and c in the equation f(x)=ax 2+bx+c. Alternately, you can use a quadratic regression, a tool available in many statistics utilities. The quadratic regression is a method similar to the method of least squares, that finds an equation for the best-fitting parabola through a set of points.

Finding a Quadratic Model (Through Three Points) To determine a unique quadratic model, you need a minimum of three non-collinear points. One way to fit a quadratic model is to identify specific points on the model and set up a system of equations. The model must allow for you to solve for a, b, and c in the equation f(x)=ax 2+bx+c. Alternately, you can use a quadratic regression, a tool available in many statistics utilities. The quadratic regression is a method similar to the method of least squares, that finds an equation for the best-fitting parabola through a set of points.

Example: The parabola below contains the points (1, -9), (6, -4), and (-0. 2, 12. 12). Find its equation. METHOD: STEPS: NOTE: When all data points lie on a single parabola, the system strategy will yield an exact model. The model found using the system will yield the same model as the quadratic regression. If the data show a quadratic trend but are not an exact fit, the equations may differ slightly.

Fitting a Quadratic through MORE than 3 Points: The table below contains data that might be collected by farmers interested in increasing the weight of their pigs. Suppose 24 randomly selected pigs were given a daily dosage (in pellets) of food supplement. Each group of three pigs received a dosage of 0 to 7 pellets, and the average percent weight gain was recorded for each pig. The table below shows the average percent weight gain for each group of three pigs in relation to the number of pellets they were given. Create a scatter plot and find the quadratic regression for this data. Are there any outliers? What does this tell about the relationship between dosage and weight gain?

More Quad. Info! There are differences when considering the application of the quadratic model in this case, as opposed to projectile motion, such as throwing a ball. Models such as this one are called impressionistic, or non-theory-based models, because no theory explains why this model fits the data.