Unionfind 1 Unionfind Maintain a collection of disjoint

Union-find 1

Union-find • Maintain a collection of disjoint sets under the following two operations • S 3 = Union(S 1, S 2) • Find(x) : returns the set containing x 2

Union-find • We assume there are n fixed elements • We start with n sets each containing a single element • Each element has a pointer to its representation in the set containing it 3

S 1 = {e 1} S 2 = {e 2} S 3={e 3} S 4={e 4} …… A = Union(S 3, S 4) S 1 = {e 1} A= {e 2, e 3} S 4={e 4} …… Find(e 2) A B = Union(A, S 7) S 1 = {e 1} B= {e 2, e 3, e 7} S 4={e 4} …… 4

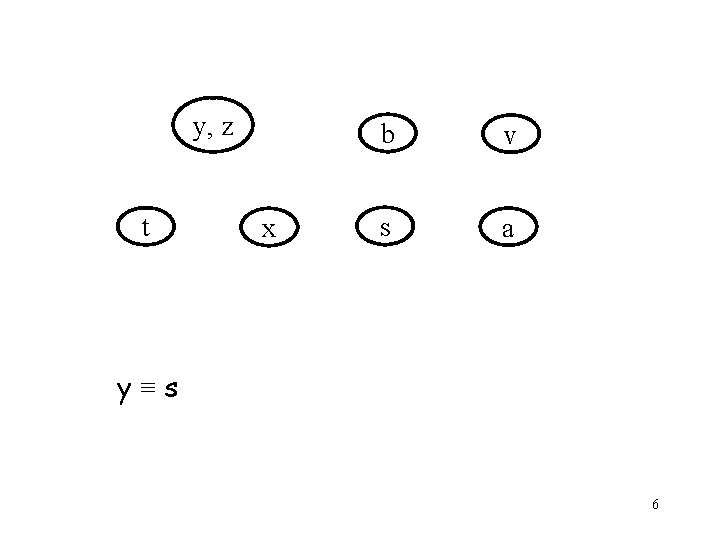
Why ? • Suppose we want to maintain an equivalence relation: y z b v t x s a y≡z 5

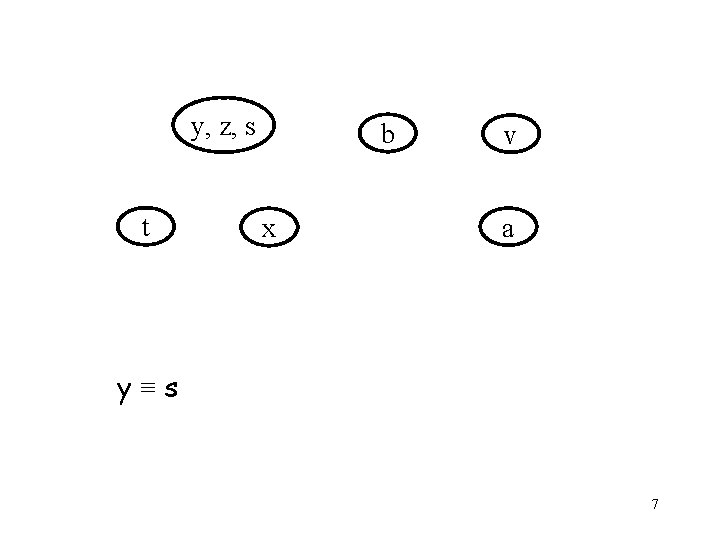
y, z t x b v s a y≡s 6

y, z, s t b x v a y≡s 7

Queries • Equivalent? (y, a) 8

Can solve this with union-find • Each equivalence class is a set • y ≡ s union(find(y), find(s)) • Equivalent? (y, a) return yes if find(y) = find(a) 9

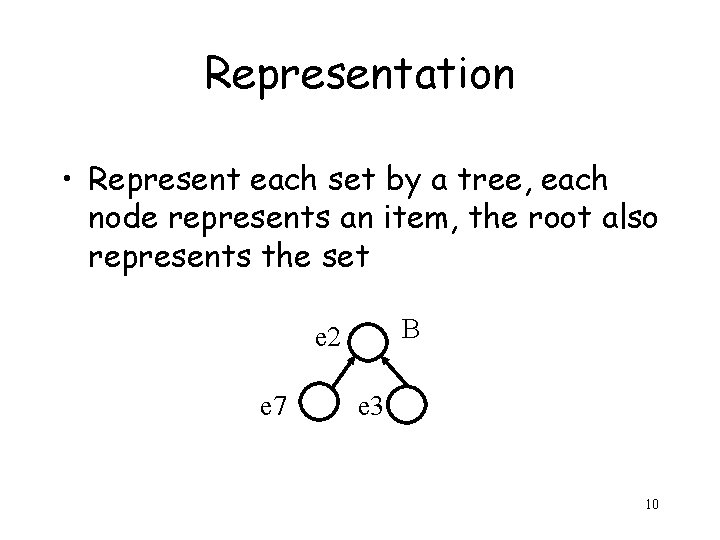
Representation • Represent each set by a tree, each node represents an item, the root also represents the set B e 2 e 7 e 3 10

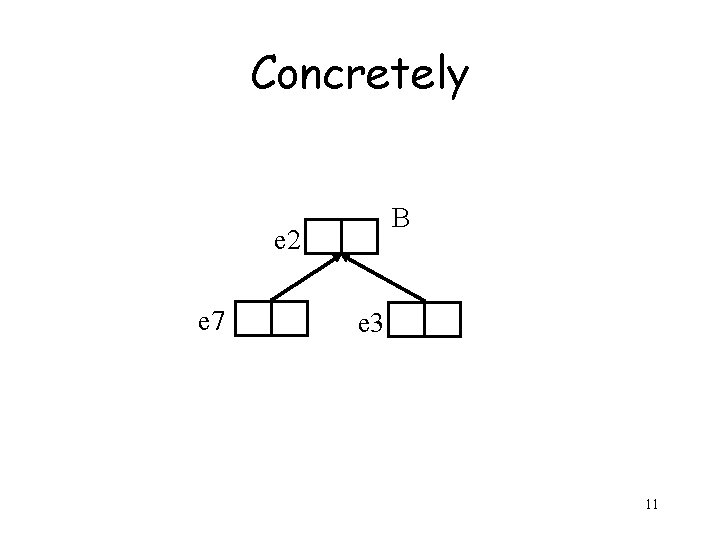
Concretely B e 2 e 7 e 3 11

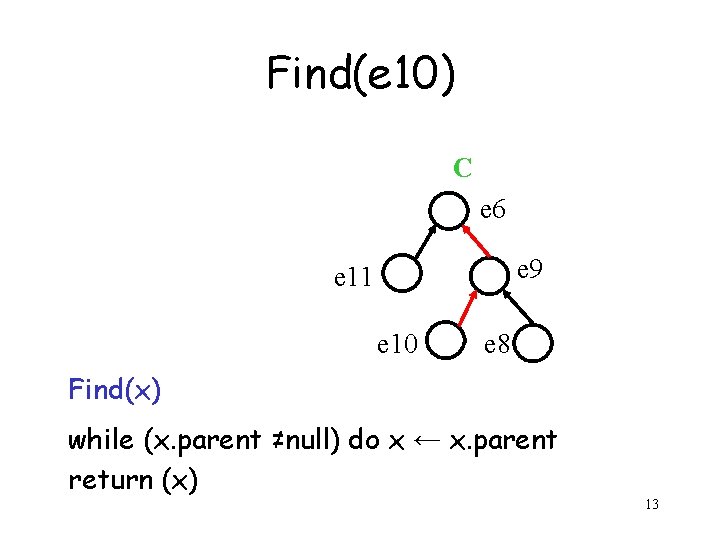
Find(e 10) C e 6 e 9 e 11 e 10 e 8 12

Find(e 10) C e 6 e 9 e 11 e 10 e 8 Find(x) while (x. parent ≠null) do x ← x. parent return (x) 13

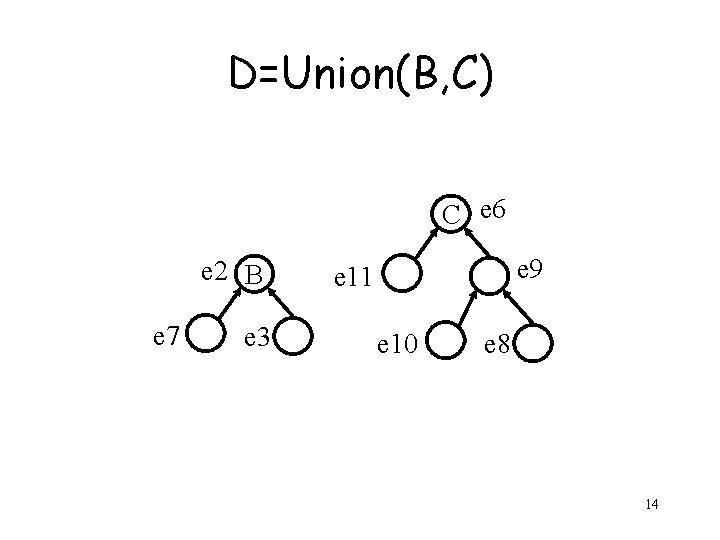
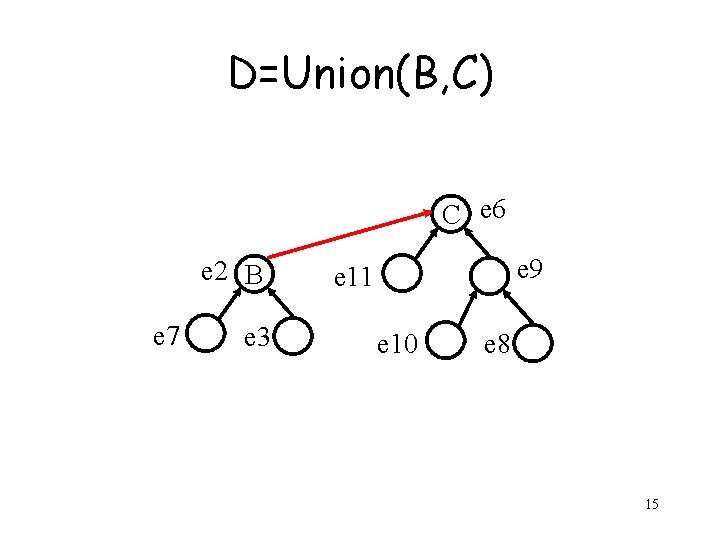
D=Union(B, C) C e 6 e 2 B e 7 e 3 e 9 e 11 e 10 e 8 14

D=Union(B, C) C e 6 e 2 B e 7 e 3 e 9 e 11 e 10 e 8 15

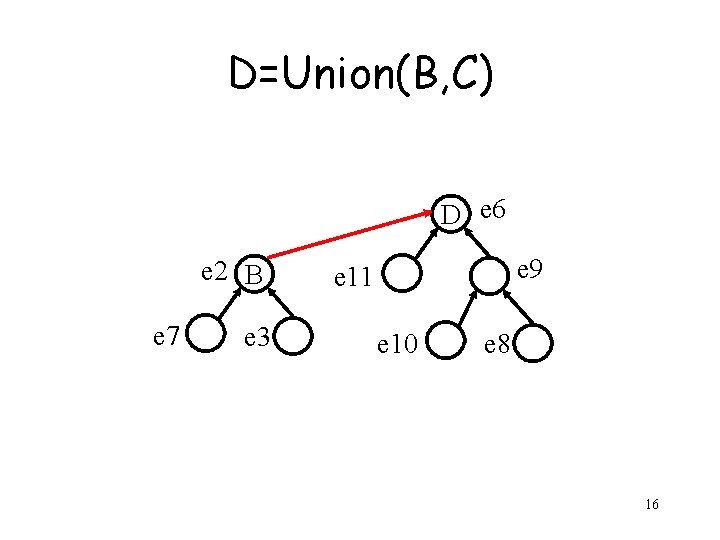
D=Union(B, C) D e 6 e 2 B e 7 e 3 e 9 e 11 e 10 e 8 16

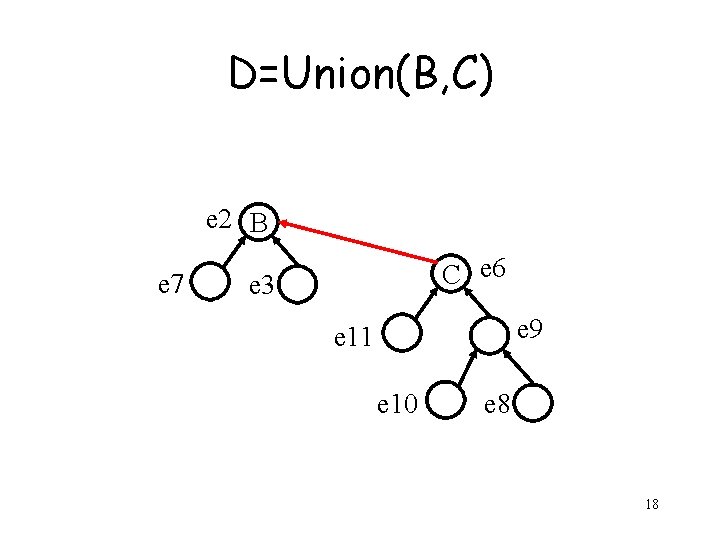
D=Union(B, C) e 2 B e 7 C e 6 e 3 e 9 e 11 e 10 e 8 17

D=Union(B, C) e 2 B e 7 C e 6 e 3 e 9 e 11 e 10 e 8 18

D=Union(B, C) e 2 D e 7 C e 6 e 3 e 9 e 11 e 10 e 8 19

Link by size • For the find’s sake its better to hang the smaller on the larger 20

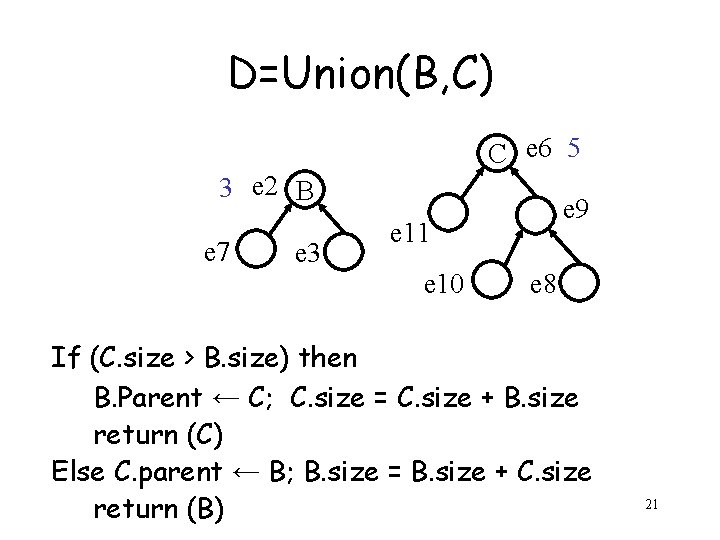
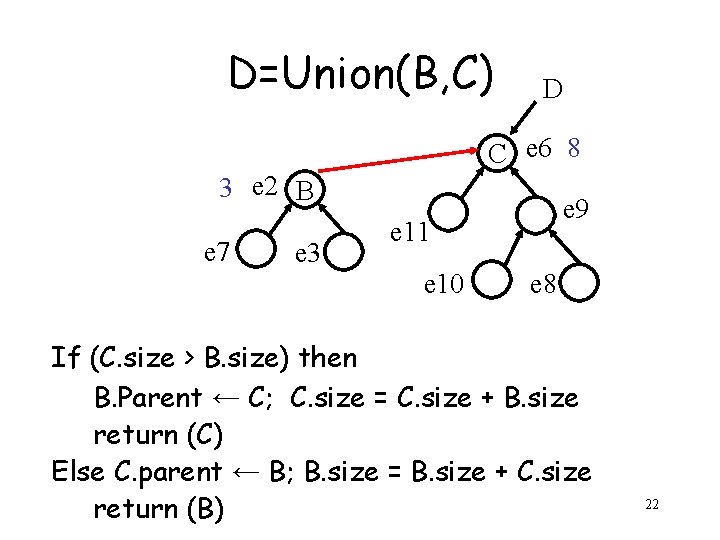
D=Union(B, C) C e 6 5 3 e 2 B e 7 e 3 e 9 e 11 e 10 e 8 If (C. size > B. size) then B. Parent ← C; C. size = C. size + B. size return (C) Else C. parent ← B; B. size = B. size + C. size return (B) 21

D=Union(B, C) D C e 6 8 3 e 2 B e 7 e 3 e 9 e 11 e 10 e 8 If (C. size > B. size) then B. Parent ← C; C. size = C. size + B. size return (C) Else C. parent ← B; B. size = B. size + C. size return (B) 22

Analysis • Union: O(1) time • Find: O(log(n)) time • The depth of a tree is at most log(n) 23

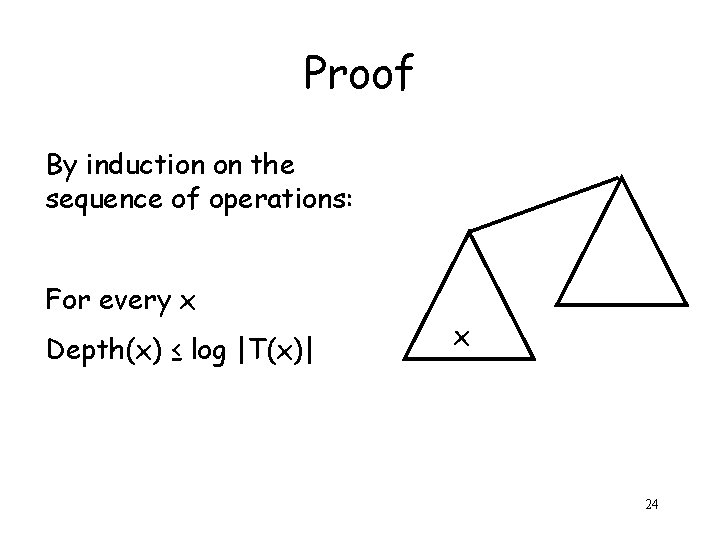
Proof By induction on the sequence of operations: For every x Depth(x) ≤ log |T(x)| x 24

Path compression 25