Uniformly Accelerated Motion Formulas and Projectiles New notations

The Oldies Remember that these formulas are ONLY GOOD for objects under UNIFORM (Constant)

Displacement Many textbooks use the letter “s” to represent displacement instead of “d” as

Velocity For final velocity, we will just use “v”. Remember this is instantaneous velocity

Acceleration must be constant for these equations to valid. Good news!! We will not

Time is time! We will not change time. We get to keep the good

New formulas for Projectiles horizontal or “x” – direction vertical or “y” – direction

Projectiles that start and end at the same height Almost every projectile problem can

Projectiles that land higher than they start vo y θ x Vertical displacement y-y

Projectiles that land lower than they start. vo Vertical displacement is “-y” Now solve

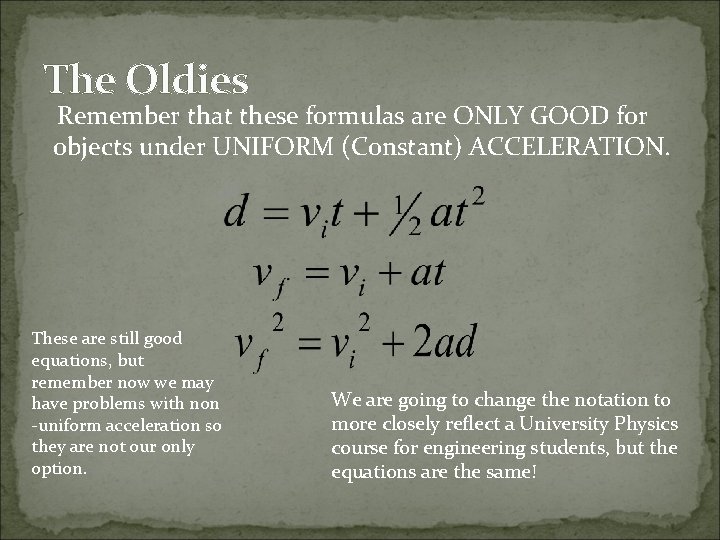
Slides: 10

Download presentation

Uniformly Accelerated Motion Formulas and Projectiles New notations for AP Physics

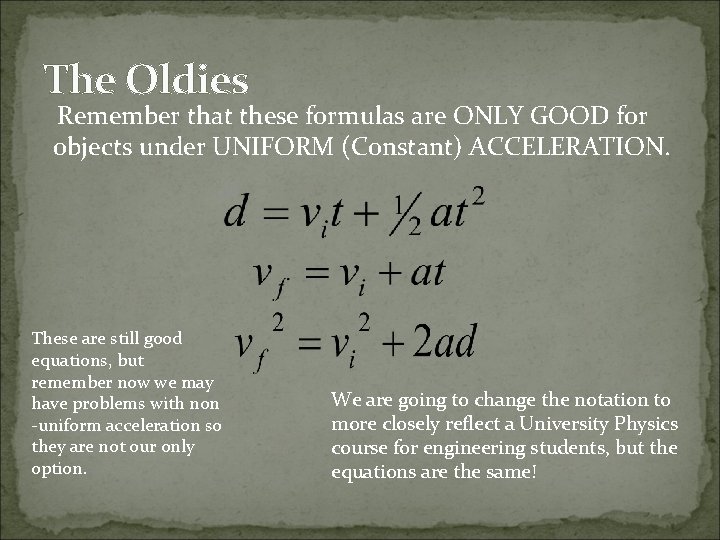
The Oldies Remember that these formulas are ONLY GOOD for objects under UNIFORM (Constant) ACCELERATION. These are still good equations, but remember now we may have problems with non -uniform acceleration so they are not our only option. We are going to change the notation to more closely reflect a University Physics course for engineering students, but the equations are the same!

Displacement Many textbooks use the letter “s” to represent displacement instead of “d” as we did in Physics 1. Others prefer to use letters that more accurately represent the position along an axis displacement such as “x”, “y” or “z”. We will be using these now…at least most of the time. Remember that displacement is a change in position. So now… Where x, y, z are the final positions along those axes, and x 0, y 0, z 0 are the initial positions along those axes.

Velocity For final velocity, we will just use “v”. Remember this is instantaneous velocity at any given time “t”, so… For initial velocity, we will use “v 0”. The “ 0” subscript refers to time “t=0” which would be the initial value.

Acceleration must be constant for these equations to valid. Good news!! We will not change the notation for acceleration…we get to keep “a”!

Time is time! We will not change time. We get to keep the good ole “t” for time. Time is the interval over which the motion of interest takes place.

New formulas for Projectiles horizontal or “x” – direction vertical or “y” – direction Remember that for projectiles, the horizontal and vertical motions must be separated analyzed independently. Remember that “ax” is zero and “ay” is acceleration due to gravity “g”. CAUTION: The equations in this form assume “up” is “positive” and “down” is “negative”.

Projectiles that start and end at the same height Almost every projectile problem can be solved by starting with the displacement equation to solve for time. In this case… vo θ Since “y” and “y 0” are both the same, vertical displacement y-y 0 = 0. Now solve for time, this will be the time for the entire flight. Remember , if you want to find maximum height you will only use half the time. If you want to find range, use the total time.

Projectiles that land higher than they start vo y θ x Vertical displacement y-y 0 = y. Now solve for time, this will be the time for the entire flight. Then you can use that time to find the horizontal distance at which it was at that height.

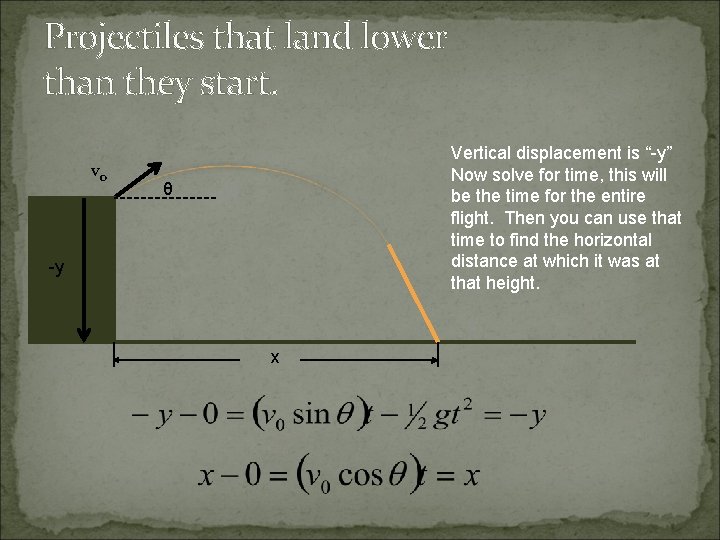
Projectiles that land lower than they start. vo Vertical displacement is “-y” Now solve for time, this will be the time for the entire flight. Then you can use that time to find the horizontal distance at which it was at that height. θ -y x