Uniform Probability Distribution The uniform distribution is a

Uniform Probability Distribution The uniform distribution is a probability distribution in which the probability of a value occurring between two points, a and b, is the same as the probability between any other two points, c and d, given that the distribution between a and b is equal to the distance between c and d.

Uniform Probability Distribution CONTINUOUS UNIFORM DISTRIBUTION where: f(x) = Value of the density function at any x value a = Lower limit of the interval from a to b b = Upper limit of the interval from a to b

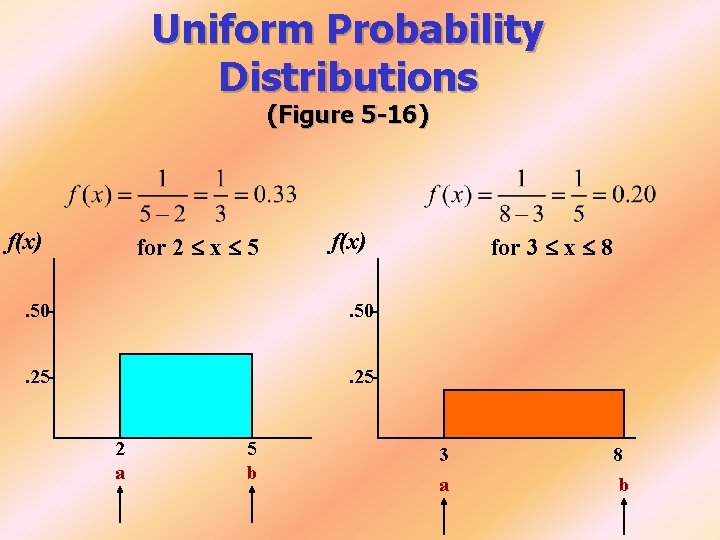
Uniform Probability Distributions (Figure 5 -16) f(x) for 2 x 5 f(x) . 50 . 25 2 a 5 b for 3 x 8 3 a 8 b

Exponential Probability Distribution The exponential probability distribution is a continuous distribution that is used to measure the time that elapses between two occurrences of an event.

Exponential Probability Distribution EXPONENTIAL DISTRIBUTION A continuous random variable that is exponentially distributed has the probability density function given by: where: e = 2. 71828. . . 1/ = The mean time between events ( >0)

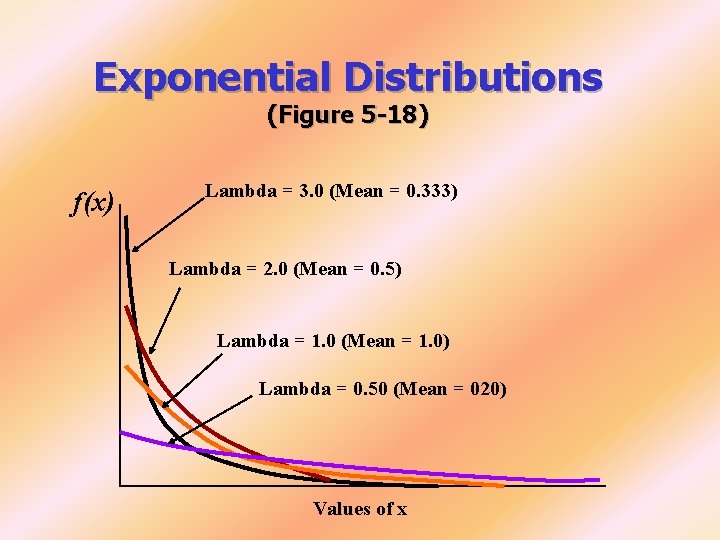
Exponential Distributions (Figure 5 -18) f(x) Lambda = 3. 0 (Mean = 0. 333) Lambda = 2. 0 (Mean = 0. 5) Lambda = 1. 0 (Mean = 1. 0) Lambda = 0. 50 (Mean = 020) Values of x

Exponential Probability EXPONENTIAL PROBABILITY