Uniform Distributions and Random Variables Lecture 23 Section

Uniform Distributions and Random Variables Lecture 23 Section 7. 5. 1 Mon, Oct 25, 2004

Uniform Distributions n Uniform distribution – A continuous distribution in which all values within a given range are equally represented in the population.

Uniform Distributions A uniform distribution must have two endpoints. n Call them a and b. n The graph of the uniform variable: n a b

Uniform Distributions A uniform distribution must have two endpoints. n Call them a and b. n The graph of the uniform variable: n a b

Uniform Distributions A uniform distribution must have two endpoints. n Call them a and b. n The graph of the uniform variable: n Area? a b

Uniform Distributions A uniform distribution must have two endpoints. n Call them a and b. n The graph of the uniform variable: n Area = 1 a b

Uniform Distributions A uniform distribution must have two endpoints. n Call them a and b. n The graph of the uniform variable: n ? Area = 1 a b

Uniform Distributions A uniform distribution must have two endpoints. n Call them a and b. n The graph of the uniform variable: n 1/(b – a) Area = 1 a b

Waiting Times A traffic light at an intersection stays red for 30 seconds. n Cars appear at the intersection at random times. n For each car that gets stopped by a red light, we observe how long it waits until the light turns green. n Let X be the waiting time. n What is the distribution of X? n
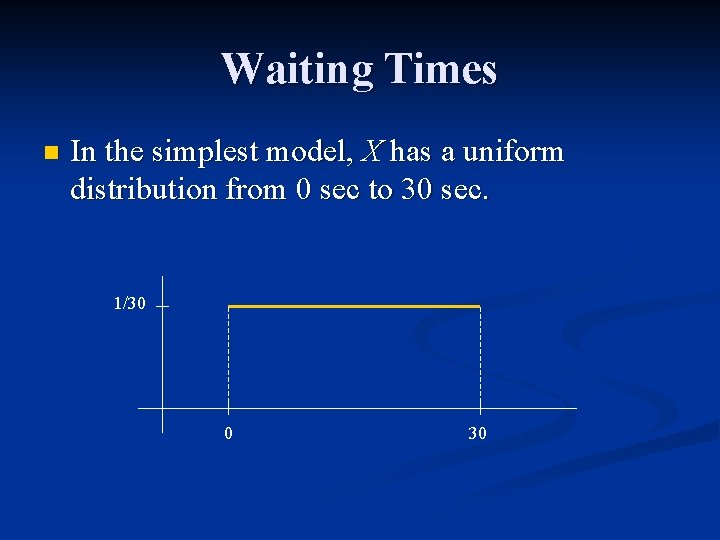
Waiting Times n In the simplest model, X has a uniform distribution from 0 sec to 30 sec. 1/30 0 30
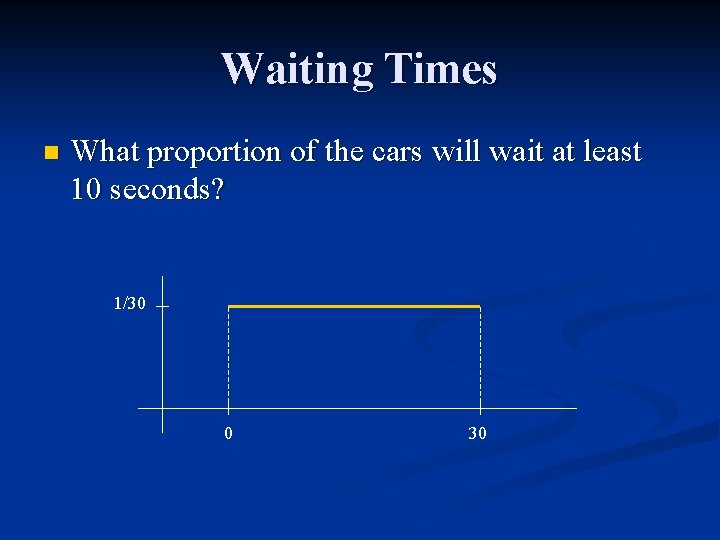
Waiting Times n What proportion of the cars will wait at least 10 seconds? 1/30 0 30
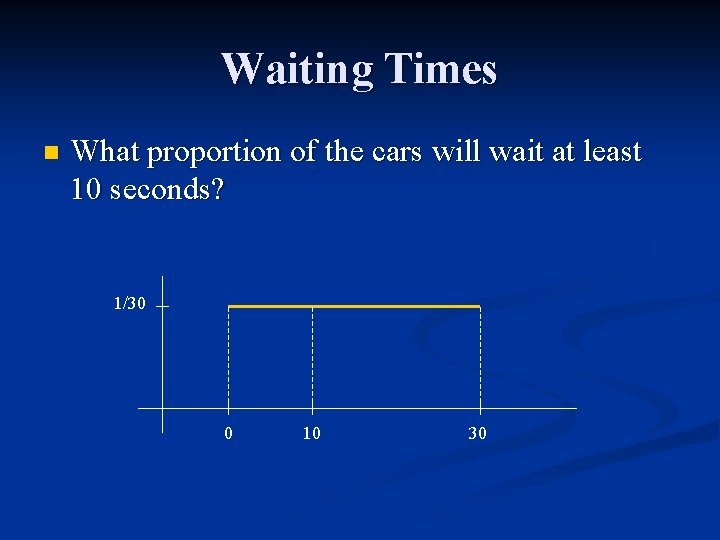
Waiting Times n What proportion of the cars will wait at least 10 seconds? 1/30 0 10 30
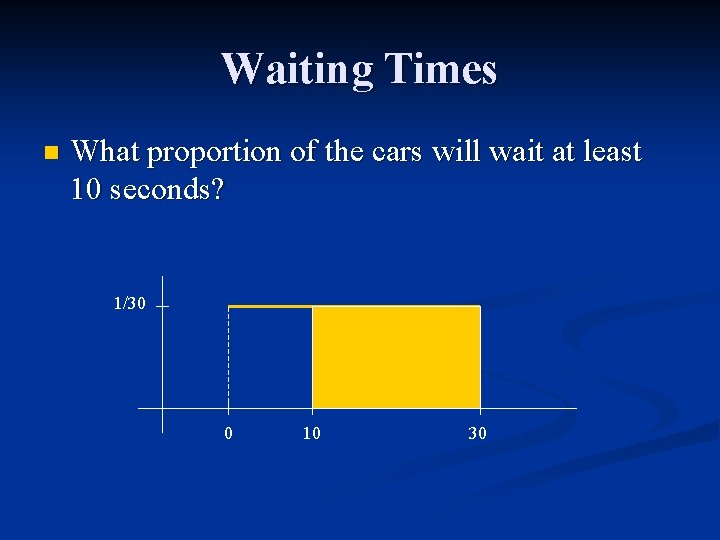
Waiting Times n What proportion of the cars will wait at least 10 seconds? 1/30 0 10 30

Waiting Times What proportion of the cars will wait at least 10 seconds? n The proportion is 20/30, or 0. 6667. n 1/30 Area = 0. 6667 0 10 30

Waiting Times n Can you think of a reason why the uniform model may not be appropriate for the situation described?

The Mean of a Uniform Variable If X is a uniform variable on the interval [a, b], then the mean of X is the midpoint (a + b)/2. n In the previous example, what is the average waiting time for the cars stopped by the red light? n

Let’s Do It! n Let’s Do It! 6. 13, p. 357 – Three Distributions.

Random Variables Random variable – A variable whose value is determined by the outcome of a procedure. n The procedure includes at least one step whose outcome is left to chance. n Therefore, the random variable takes on a new value each time the procedure is performed. n

A Note About Probability The probability that something happens is the proportion of the time that it does happen out of all the times it was given an opportunity to happen. n Therefore, “probability” and “proportion” are synonymous in the context of what we are doing. n

Examples of Random Variables n Roll two dice. Let X be the number of sixes. n n Roll two dice. Let X be the total of the two numbers. n n Possible values of X = {0, 1, 2}. Possible values of X = {2, 3, 4, …, 12}. Select a person at random and give him up to one hour to perform a simple task. Let X be the time it takes him to perform the task. n Possible values of X are {x | 0 ≤ x ≤ 1}.

Types of Random Variables Discrete Random Variable – A random variable whose set of possible values is a discrete set. n Continuous Random Variable – A random variable whose set of possible values is a continuous set. n In the previous examples, are they discrete or continuous? n

Discrete Probability Distribution Functions n Discrete Probability Distribution Function (pdf) – A function that assigns a probability to each possible value of a discrete random variable.

Example of a Discrete PDF Roll two dice and let X be the number of sixes. n Draw the 6 6 rectangle showing all 36 possibilities. (1, 1) (1, 2) (1, 3) (1, 4) (1, 5) (1, 6) n From it we see that n P(X = 0) = 25/36. n P(X = 1) = 10/36. n P(X = 2) = 1/36. n (2, 1) (2, 2) (2, 3) (2, 4) (2, 5) (2, 6) (3, 1) (3, 2) (3, 3) (3, 4) (3, 5) (3, 6) (4, 1) (4, 2) (4, 3) (4, 4) (4, 5) (4, 6) (5, 1) (5, 2) (5, 3) (5, 4) (5, 5) (5, 6) (6, 1) (6, 2) (6, 3) (6, 4) (6, 5) (6, 6)

Example of a Discrete PDF Suppose that 10% of all households have no children, 30% have one child, 40% have two children, and 20% have three children. n Select a household at random and let X = number of children. n Then X is a random variable. n Which step in the procedure is left to chance? n What is the pdf of X? n

Example of a Discrete PDF n We may present the pdf as a table. x 0 1 2 3 P (X = x ) 0. 10 0. 30 0. 40 0. 20
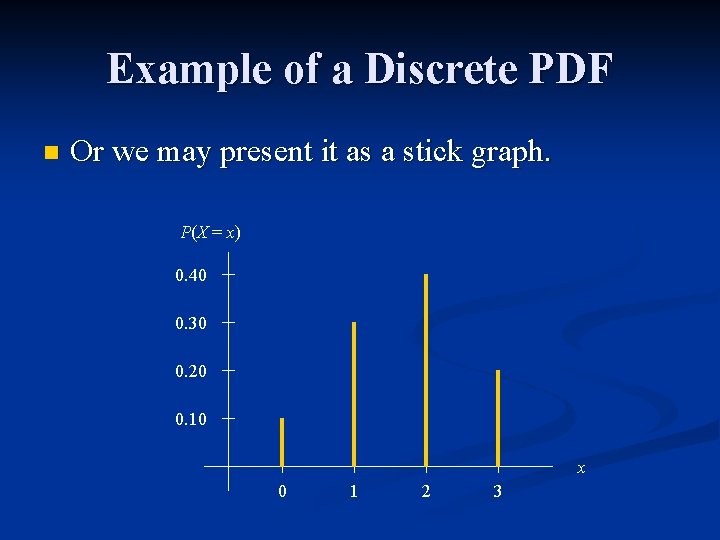
Example of a Discrete PDF n Or we may present it as a stick graph. P(X = x) 0. 40 0. 30 0. 20 0. 10 x 0 1 2 3
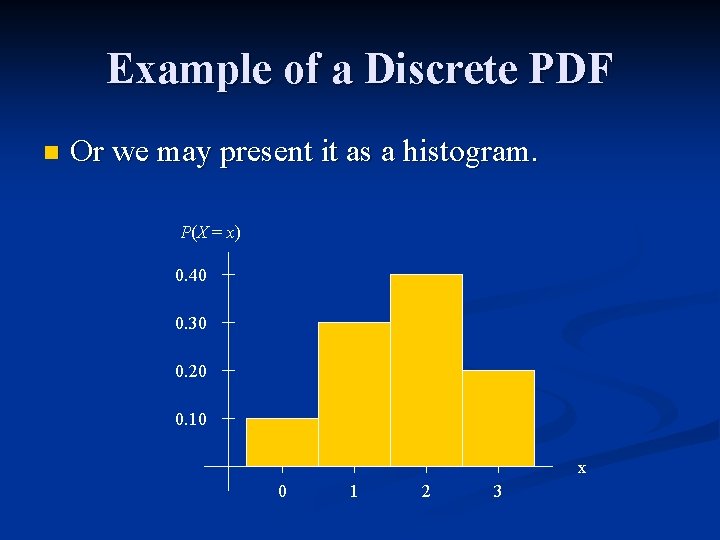
Example of a Discrete PDF n Or we may present it as a histogram. P(X = x) 0. 40 0. 30 0. 20 0. 10 x 0 1 2 3

Let’s Do It! n Let’s do it! 7. 20, p. 426 – Sum of Pips.
- Slides: 28