Uniform Cost Search UCS Intuition Find shortest path

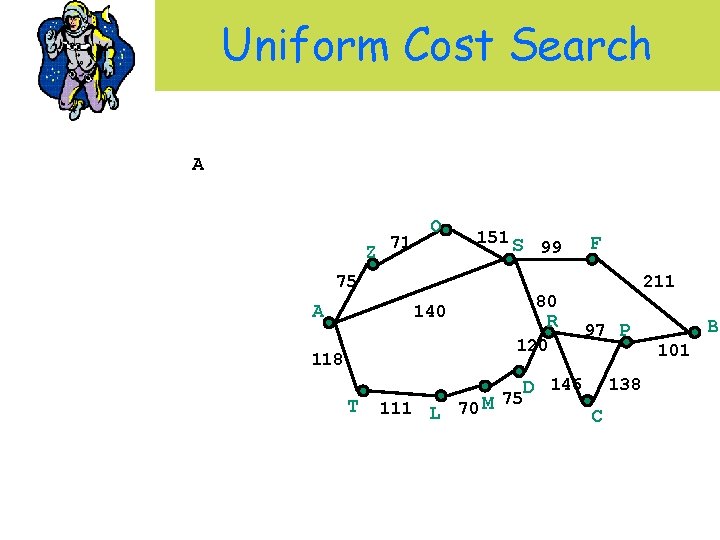
Uniform Cost Search • UCS Intuition: Find shortest path in terms of sum of lengths of sub-paths. • Agenda: priority queue ordered by path length; get shortest path in queue. • Will it get the shortest path? • Optimal and complete Z 71 A 75 O 151 S T 111 211 R 140 118 99 F 80 97 P B 120 146 101 138 D 70 M 75 L C

Uniform Cost Search A Z 71 O 151 S 75 A 99 R 120 T 111 L 70 M 211 80 140 118 F 97 P D 146 75 138 C B 101

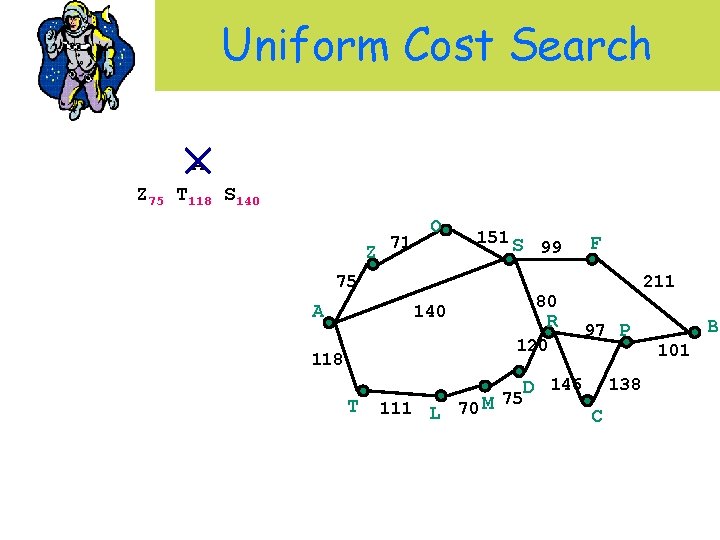
Uniform Cost Search A Z 75 T 118 S 140 Z 71 O 151 S 75 A 99 R 120 T 111 L 70 M 211 80 140 118 F 97 P D 146 75 138 C B 101

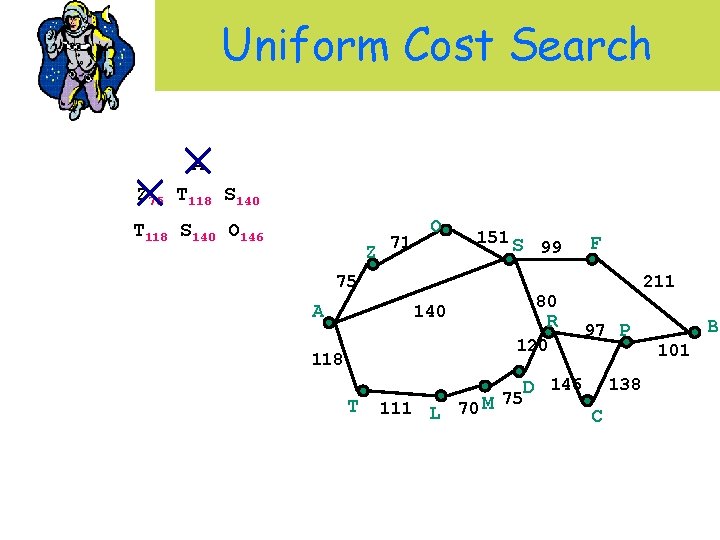
Uniform Cost Search A Z 75 T 118 S 140 O 146 Z 71 O 151 S 75 A 99 R 120 T 111 L 70 M 211 80 140 118 F 97 P D 146 75 138 C B 101

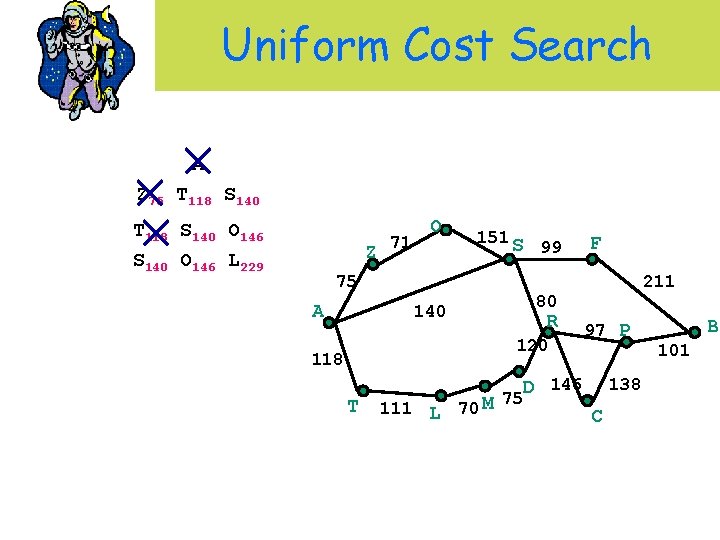
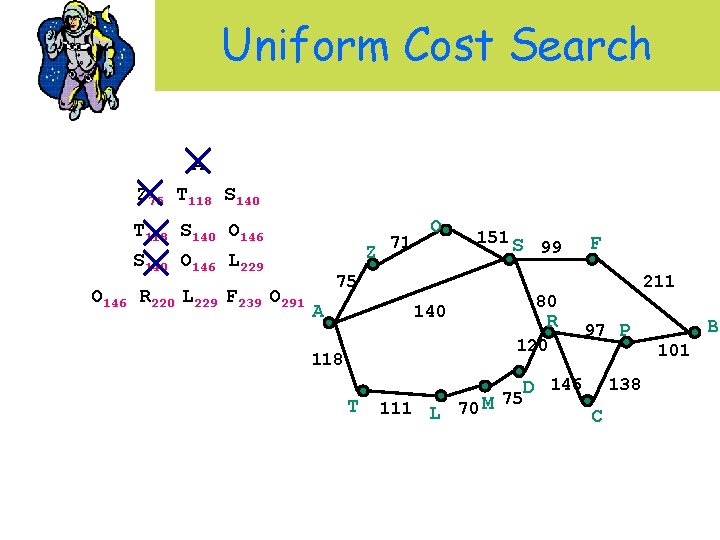
Uniform Cost Search A Z 75 T 118 S 140 O 146 L 229 Z 71 O 151 S 75 A 99 R 120 T 111 L 70 M 211 80 140 118 F 97 P D 146 75 138 C B 101

Uniform Cost Search A Z 75 T 118 S 140 O 146 L 229 O 146 R 220 L 229 F 239 O 291 Z 71 O 151 S 75 A 99 R 120 T 111 L 70 M 211 80 140 118 F 97 P D 146 75 138 C B 101

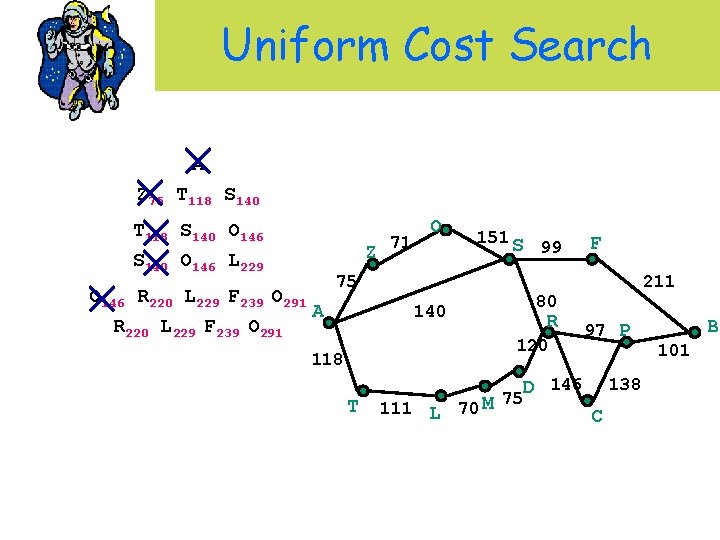
Uniform Cost Search A Z 75 T 118 S 140 O 146 L 229 Z O 146 R 220 L 229 F 239 O 291 A R 220 L 229 F 239 O 291 71 O 151 S 75 99 R 120 T 111 L 70 M 211 80 140 118 F 97 P D 146 75 138 C B 101

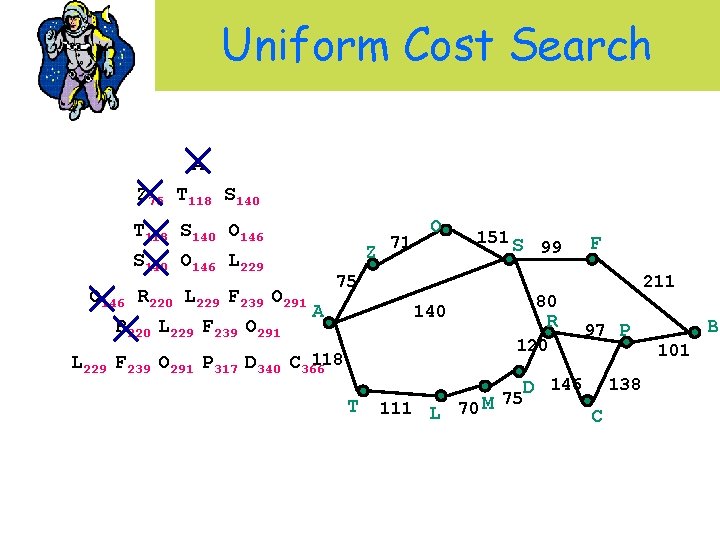
Uniform Cost Search A Z 75 T 118 S 140 O 146 L 229 O 146 R 220 L 229 F 239 O 291 A R 220 L 229 F 239 O 291 Z 71 O 151 S 75 99 R 120 T 111 L 70 M 211 80 140 118 L 229 F 239 O 291 P 317 D 340 C 366 F 97 P D 146 75 138 C B 101

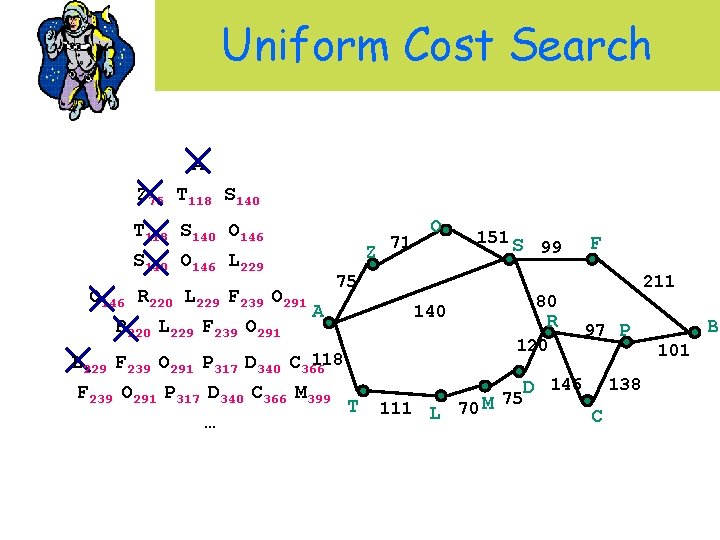
Uniform Cost Search A Z 75 T 118 S 140 O 146 L 229 O 146 R 220 L 229 F 239 O 291 A R 220 L 229 F 239 O 291 Z 71 O 151 S 75 118 L 229 F 239 O 291 P 317 D 340 C 366 M 399 T … 99 211 80 140 R 120 111 L 70 M F 97 P D 146 75 138 C B 101

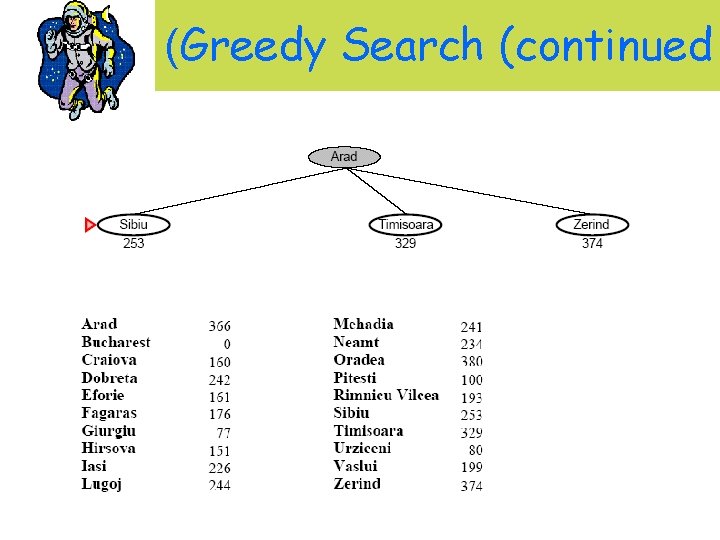
Greedy Search Example

(Greedy Search (continued

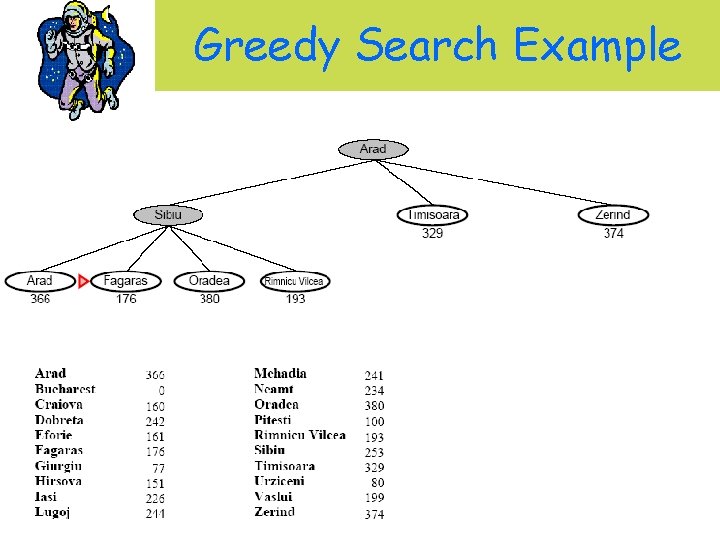
Greedy Search Example

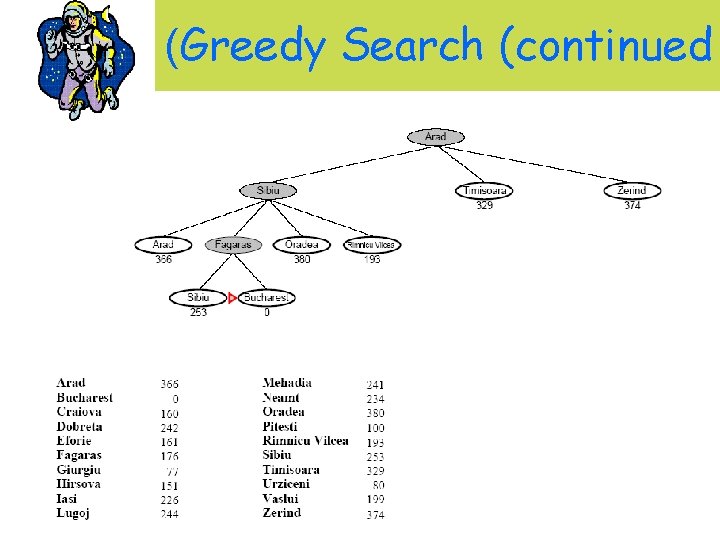
(Greedy Search (continued

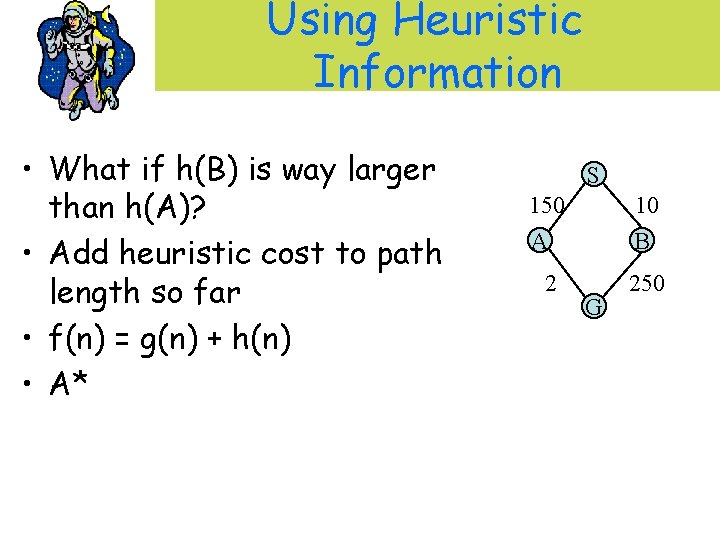
Using Heuristic Information • What if h(B) is way larger than h(A)? • Add heuristic cost to path length so far • f(n) = g(n) + h(n) • A* S 150 A 10 B 2 250 G

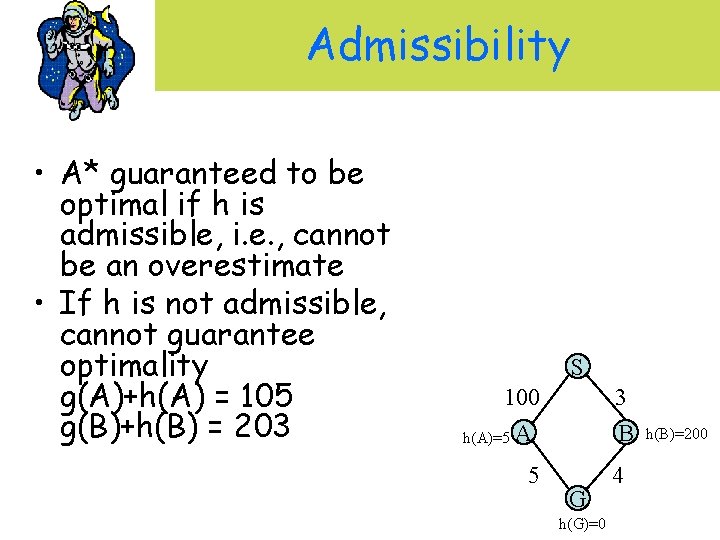
Admissibility • A* guaranteed to be optimal if h is admissible, i. e. , cannot be an overestimate • If h is not admissible, cannot guarantee optimality g(A)+h(A) = 105 g(B)+h(B) = 203 S 100 h(A)=5 A 5 3 B G h(G)=0 4 h(B)=200

Heuristic for Path. Planning Problem: SLD • Is straight-line distance (SLD) an admissible heuristic for path planning? • Triangle inequality |AC| < |AB|+|BC| • Admissible!

Graph Search Requires !Consistency as well • Consistency: h(n) ≤ c(n, n') + h(n'), where n' is a successor of n • Graph search is optimal if h(n) is consistent • If h(n) is consistent then f(n) is a monotonically n increasing function c(n, n') n' h(n') h(n) G

Selecting a Heuristic • Heuristic should cut down on search space. • Can find heuristic by relaxing the problem • Heuristic functions can be solutions to “relaxed” version of original • Procedure: Relax hard problem so it’s easy to solve; use solution to relaxed problem as heuristic for real problem.

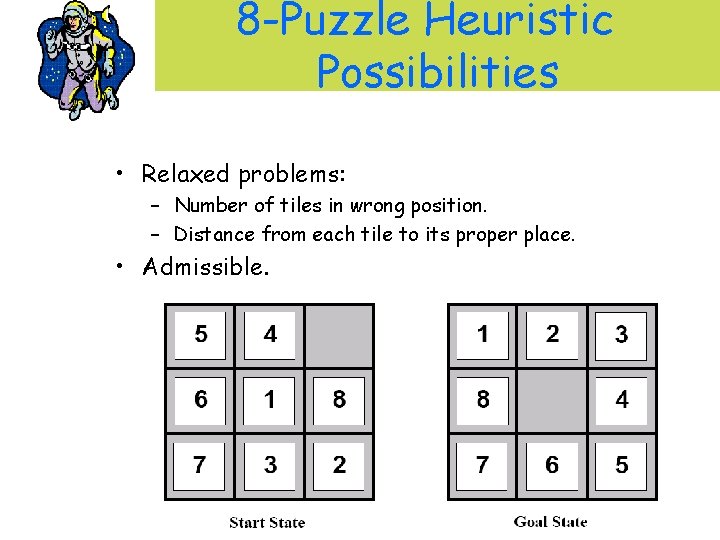
8 -Puzzle Heuristic Possibilities • Relaxed problems: – Number of tiles in wrong position. – Distance from each tile to its proper place. • Admissible.

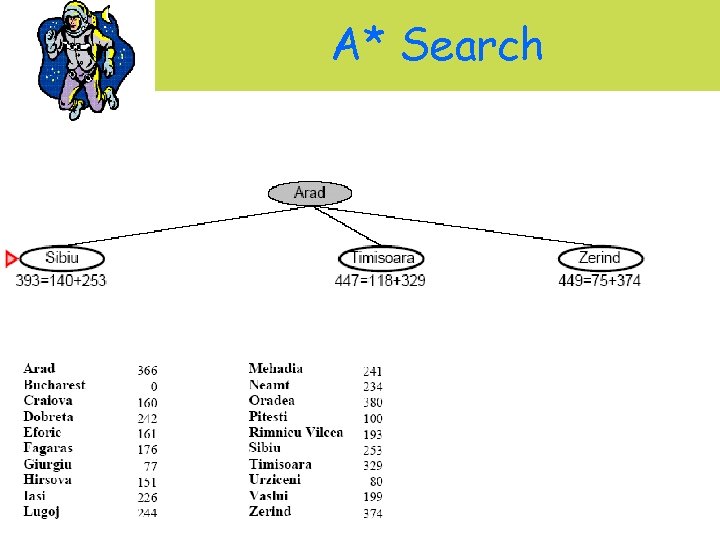
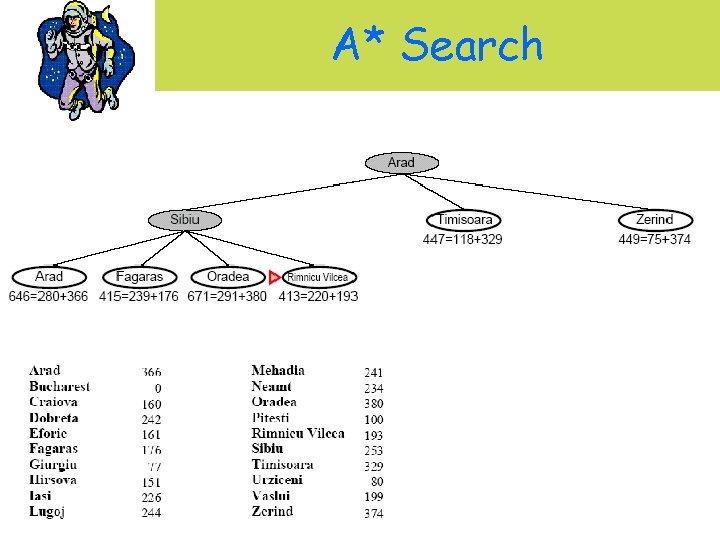
A* Search

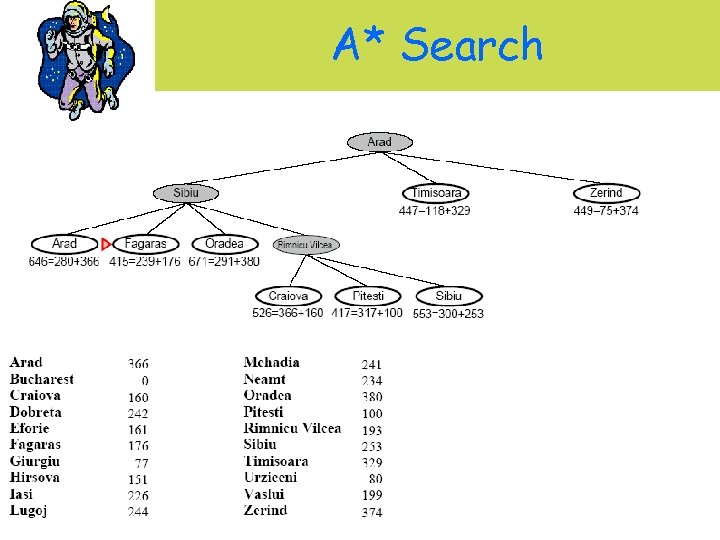
A* Search

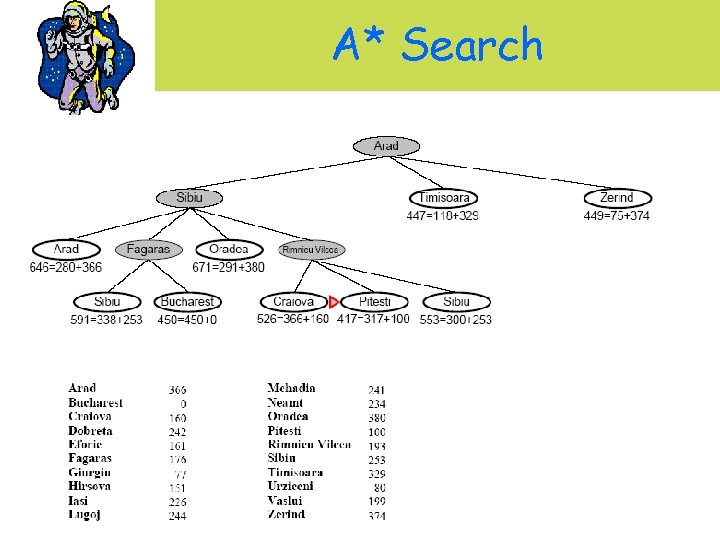
A* Search

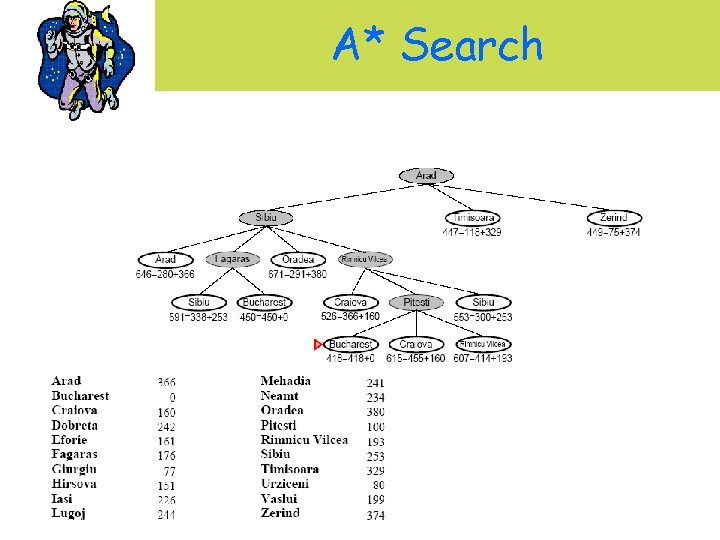
A* Search

A* Search

Norvig’s Lisp – tree search (defun tree-search (states goal-p successors combiner) "Find a state that satisfies goal-p. Start with states, and search according to successors and combiner. " (dbg : search "~&; ; Search: ~a" states) (cond ((null states) fail) ((funcall goal-p (first states)) (t (tree-search (funcall combiner (funcall successors (first states)) (rest states)) goal-p successors combiner))))

DFS, BFS (defun depth-first-search (start goal-p successors) "Search new states first until goal is reached. " (tree-search (list start) goal-p successors #'append)) (defun binary-tree (x) (list (* 2 x) (+ 1 (* 2 x)))) (defun is (value) #'(lambda (x) (eql x value))) (defun prepend (x y) "Prepend y to start of x" (append y x)) (defun breadth-first-search (start goal-p successors) "Search old states first until goal is reached. " (tree-search (list start) goal-p successors #'prepend)) (defun finite-binary-tree (n) "Return a successor function that generates a binary tree with n nodes. " #'(lambda (x) (remove-if #'(lambda (child) (> child n)) (binary-tree x))))

Best First Search (defun diff (num) "Return the function that finds the difference from num. " #'(lambda (x) (abs (- x num)))) (defun sorter (cost-fn) "Return a combiner function that sorts according to cost-fn. " #'(lambda (new old) (sort (append new old) #'< : key cost-fn))) (defun best-first-search (start goal-p successors cost-fn) "Search lowest cost states first until goal is reached. " (tree-search (list start) goal-p successors (sorter cost-fn)))

Beam Search (defun beam-search (start goal-p successors cost -fn beam-width) "Search highest scoring states first until goal is reached, but never consider more than beam-width states at a time. " (tree-search (list start) goal-p successors #'(lambda (old new) (let ((sorted (funcall (sorter cost-fn) old new))) (if (> beam-width (length sorted)) sorted (subseq sorted 0 beam-width))))))