Uniform circular motion Proof of Eq 4 34

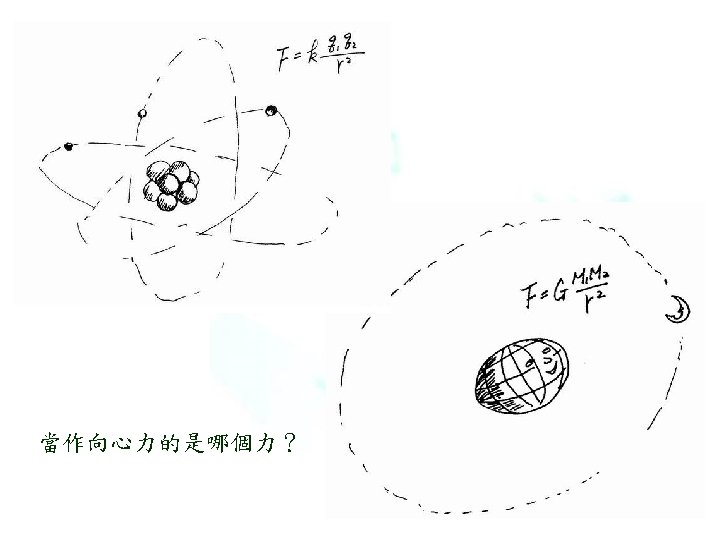
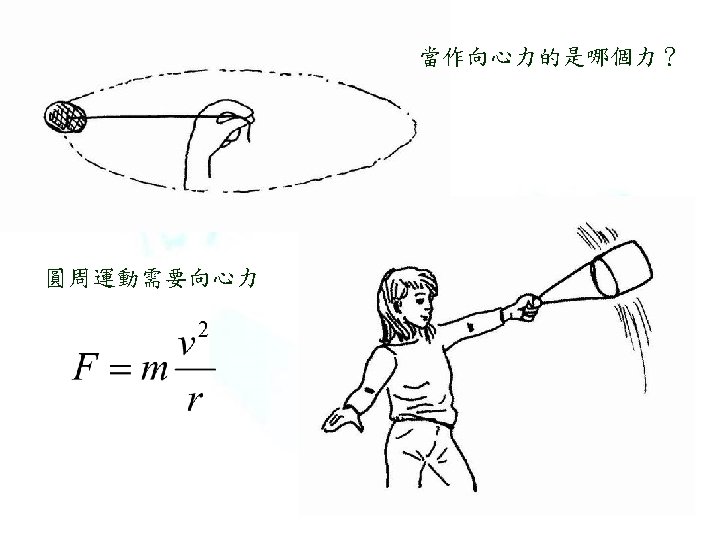
Uniform circular motion 圓周運動需要向心力。 證明

Proof of Eq. 4 -34

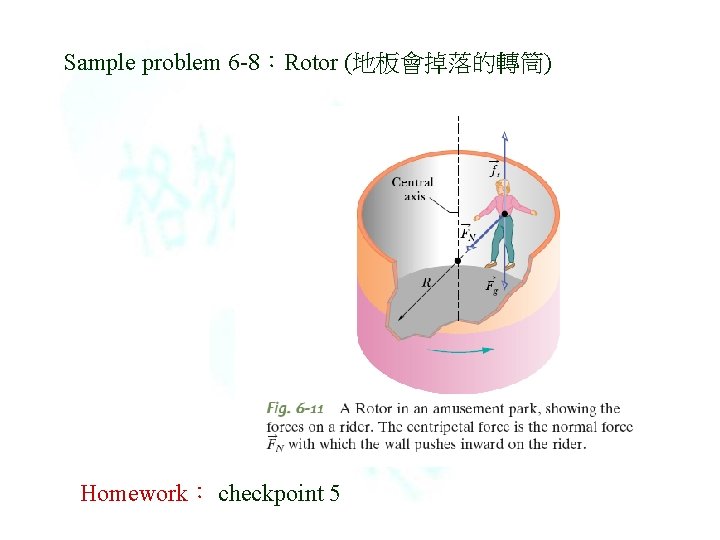
等速率圓周運動 Uniform circular motion • 向心加速度 a = v 2/r (證明) – Homework ：Bohr mode（補充習題103 -1） • rounding a curve in a car：車子轉彎時，座位上的人為什麼會 滑動？ – Homework : 翻譯 rounding a curve in a car這一段課文（ p 124 ~125） • orbiting the earth（太空中的失重） – 自由落體時的失重 – Sample problem 6 -6 • Rotor (地板會掉落的轉筒) – Sample problem 6 -8 – Homework： checkpoint 5

補充習題 103 -1（Bohr model） In the Bohr model of the hydrogen atom, the electron revolves in a circular orbit around the nucleus. If the radius is 5. 3× 10 -11 m and the electron circles 6. 6× 1015 times per second, find (a) the speed of the electron, (b) the acceleration (magnitude and direction) of the electron, and (c) the centripetal force acting on electron. The electron's mass is 9. 11× 10 -31 kg. Bohr(1885~1962)

Sample problem 6 -8：Rotor (地板會掉落的轉筒) Homework： checkpoint 5

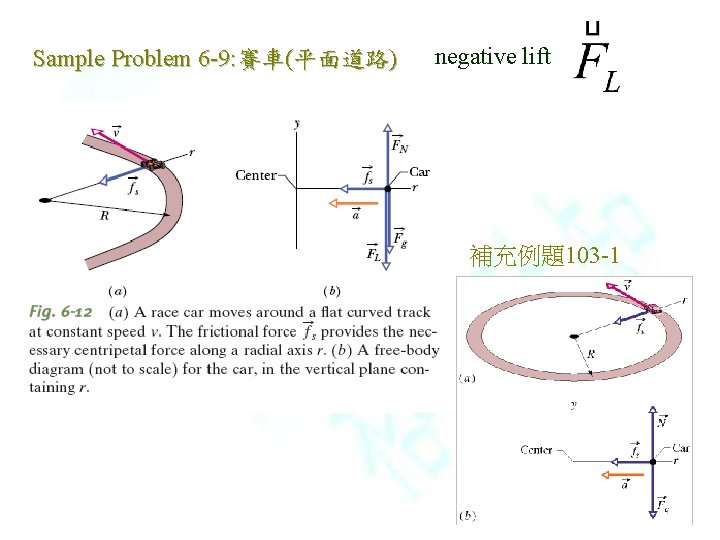
補充例題103 -1: 賽車（平面道路） The figure represents a stock car of mass m = 1600 kg traveling at a constant speed v = 20 m/s around a flat, circular track of radius R = 190 m. For what value of μs between the track and the tires of the car will the car be on the verge of sliding off the track? 寫出力的關係式 Ans. μs=0. 21 這是輪胎與路面間之最“小”或 “大 ”靜摩擦係數？ 如果現在車速增加，靜摩擦係數 會怎樣？

Sample Problem 6 -9: 賽車(平面道路) negative lift 補充例題103 -1

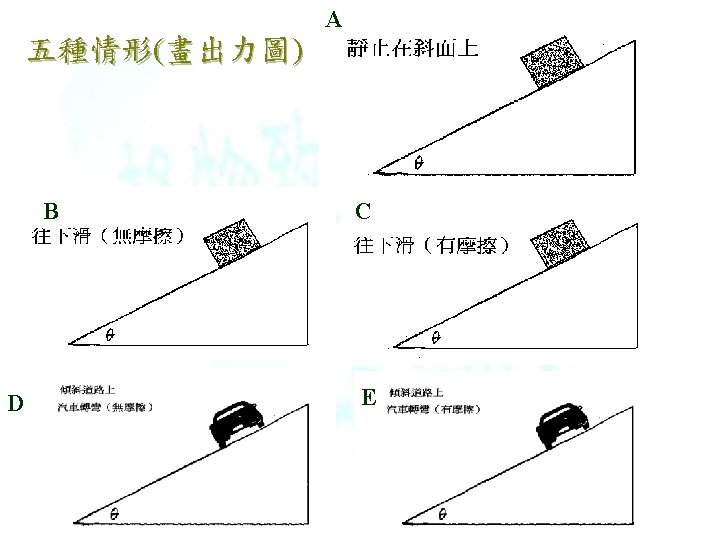
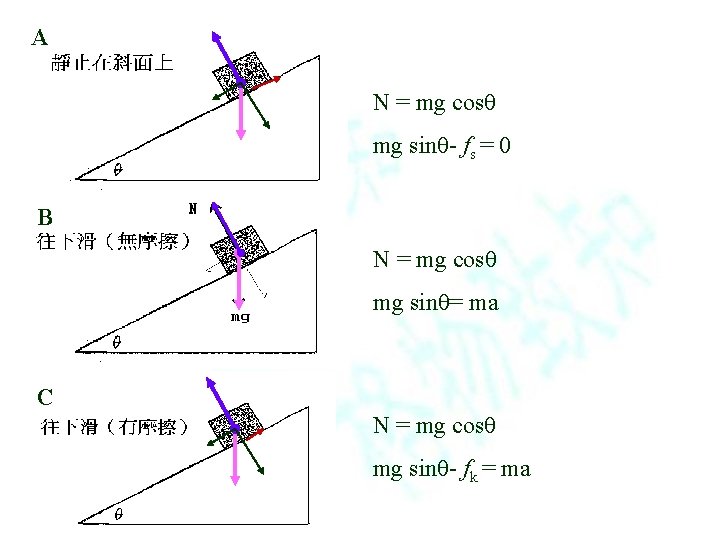
A N = mg cosθ mg sinθ- fs = 0 B N = mg cosθ mg sinθ= ma C N = mg cosθ mg sinθ- fk = ma

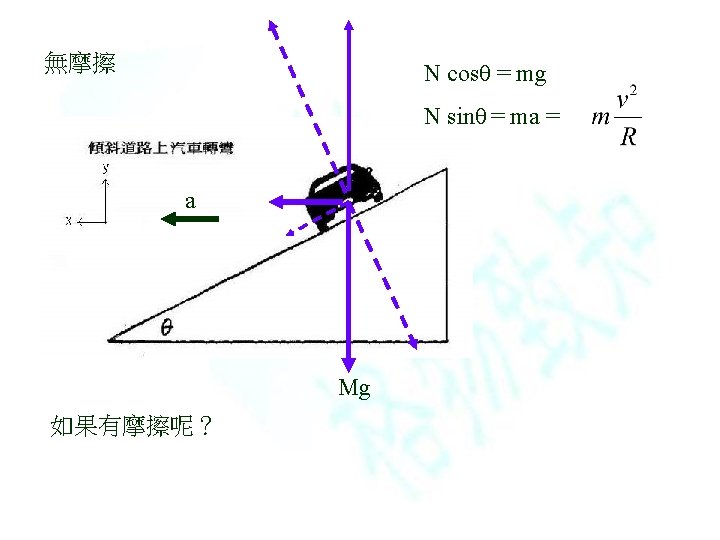
D E

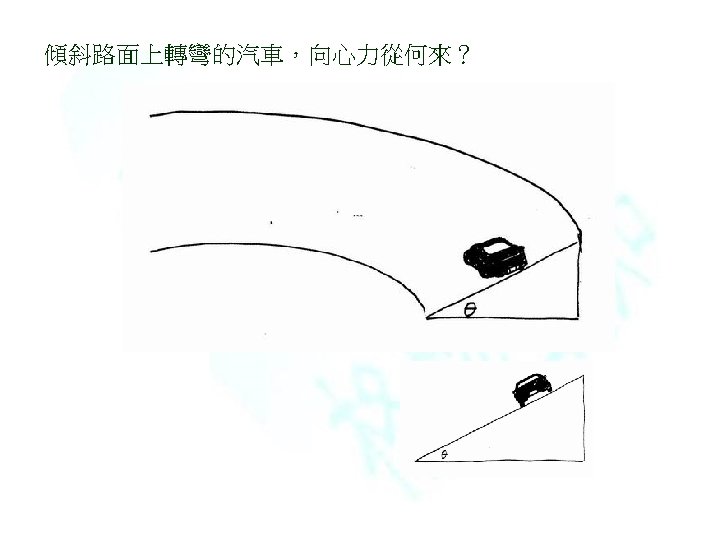
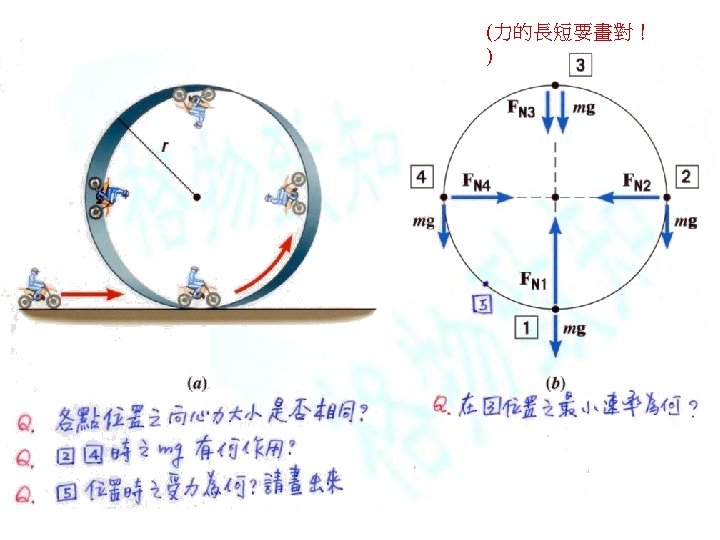
(傾斜道路轉彎，有摩擦) (力的長短要畫對！ ) Homework : Ch 6, problem 72 Homework : Ch 6, problem 50 Homework : Ch 6, problem 54

Ch 6, Problem 50 A banked circular highway curve is designed for traffic moving at 60 km/h. The radius of the curve is 200 m. Traffic is moving along the highway at 40 km/h on a rainy day. What is the minimum coefficient of friction between tires and road that will allow cars to take the turn without sliding off the road? (Assume the cars do not have negative lift. )

Ch 6, Problem 54 Engineering a highway curve. If a car goes through a curve too fast, the car tends to slide out of the curve. For a banked curve with friction, a frictional force acts on a fast car to oppose the tendency to slide out of the curve; the force is directed down the bank (in the direction water would drain). Consider a circular curve of radius R=200 m and bank angleθ, where the coefficient of static friction between tires and pavement is μs. A car (without negative lift) is driven around the curve as shown in Fig. 613. (a) Find an expression for the car speed vmax that puts the car on the verge of sliding out. (b) On the same graph, plot vmax versus angleθ for the range 0 o to 50 o, first for μs =0. 60 (dry pavement) and then forμs = 0. 050 (wet or icy pavement). In kilometers per hour, evaluate vmax for a bank angle of 10 o and for (c) μs = 0. 60 and (d) μs = 0. 050. (Now you can see why accidents occur in highway curves when icy conditions are not obvious to drivers, who tend to drive at normal speeds. )

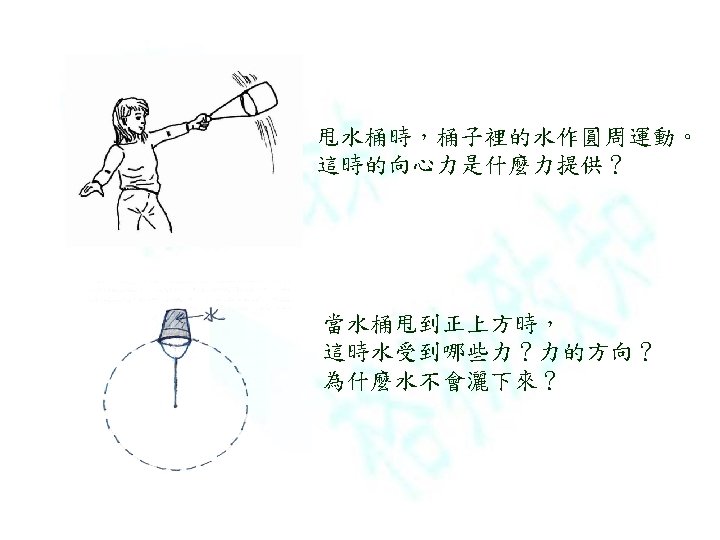
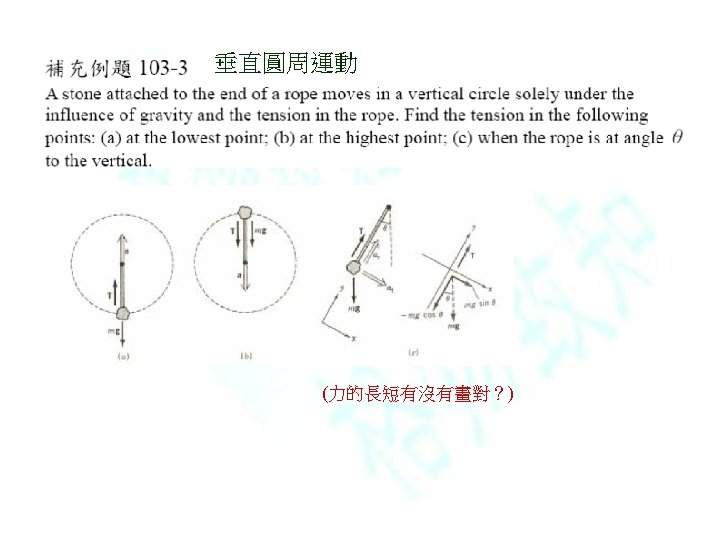
垂直圓周運動(Vertical circular motion ) • 甩水桶 • Sample problem 6 -7: loop-the-loop – 墾丁福華 星際碼頭 踩腳踏車 – Homework：check point 4: Ferris wheel 摩天輪 • 補充例題 103 -3：垂直圓周運動