Uniform and Normal Distributions Chp 6 Uniform and

Uniform and Normal Distributions Chp. 6 Uniform and Normal EGR 252 Slide 1

Continuous Probability Distributions • Many continuous probability distributions, including: ü Uniform ü Normal ü Gamma ü Exponential ü Chi-Squared ü Lognormal ü Weibull PDF Chp. 6 Uniform and Normal Source: www. itl. nist. gov EGR 252 Slide 2

Uniform Distribution • Simplest – characterized by the interval endpoints, A and B. A≤x≤B =0 elsewhere • Mean and variance: and Chp. 6 Uniform and Normal EGR 252 Slide 3

Example: Uniform Distribution A circuit board failure causes a shutdown of a computing system until a new board is delivered. The delivery time X is uniformly distributed between 1 and 5 days. What is the probability that it will take 2 or more days for the circuit board to be delivered? Chp. 6 Uniform and Normal EGR 252 Slide 4

In Class Examples • 6. 3 Chp. 6 Uniform and Normal EGR 252 Slide 5

Normal Distribution • The “bell-shaped curve” • Also called the Gaussian distribution • The most widely used distribution in statistical analysis ü forms the basis for most of the parametric tests we’ll perform later in this course. ü describes or approximates most phenomena in nature, industry, or research • Random variables (X) following this distribution are called normal random variables. ü the parameters of the normal distribution are μ and σ (sometimes μ and σ2. ) Chp. 6 Uniform and Normal EGR 252 Slide 6

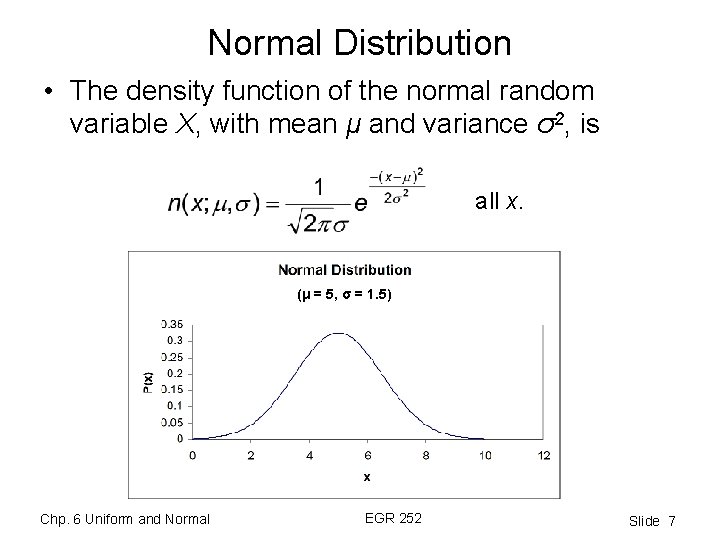
Normal Distribution • The density function of the normal random variable X, with mean μ and variance σ2, is all x. (μ = 5, σ = 1. 5) Chp. 6 Uniform and Normal EGR 252 Slide 7

Standard Normal RV … • Note: the probability of X taking on any value between x 1 and x 2 is given by: • To ease calculations, we define a normal random variable where Z is normally distributed with μ = 0 and σ2 = 1 Chp. 6 Uniform and Normal EGR 252 Slide 8

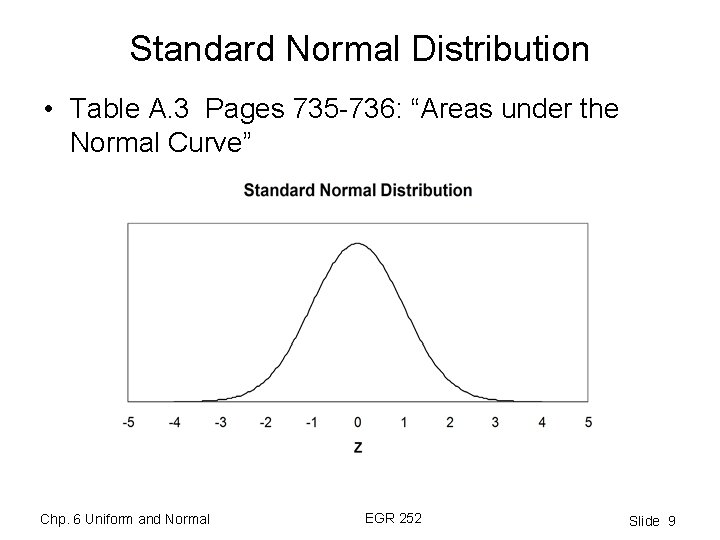
Standard Normal Distribution • Table A. 3 Pages 735 -736: “Areas under the Normal Curve” Chp. 6 Uniform and Normal EGR 252 Slide 9

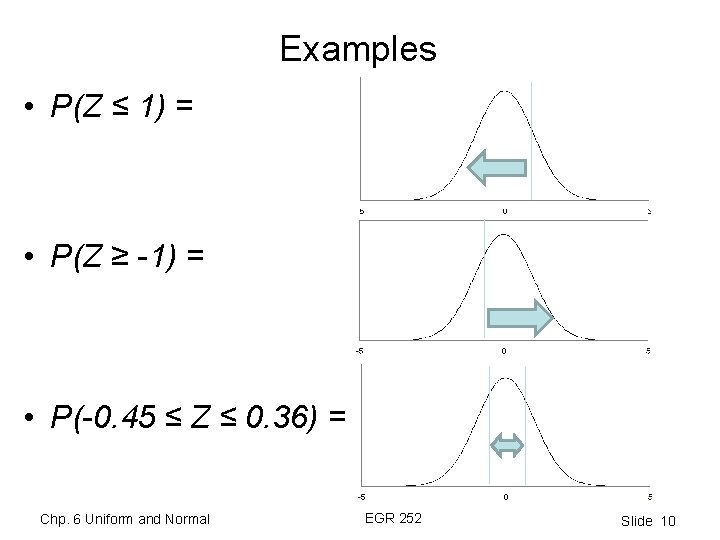
Examples • P(Z ≤ 1) = • P(Z ≥ -1) = • P(-0. 45 ≤ Z ≤ 0. 36) = Chp. 6 Uniform and Normal EGR 252 Slide 10

Name: ____________ • Use Table A. 3 to determine (draw the picture!) 1. P(Z ≤ 0. 8) = 2. P(Z ≥ 1. 96) = 3. P(-0. 25 ≤ Z ≤ 0. 15) = 4. P(Z ≤ -2. 0 or Z ≥ 2. 0) = Chp. 6 Uniform and Normal EGR 252 Slide 11

Applications of the Normal Distribution • A certain machine makes electrical resistors having a mean resistance of 40 ohms and a standard deviation of 2 ohms. What percentage of the resistors will have a resistance less than 44 ohms? • Solution: X is normally distributed with μ = 40 and σ = 2 and x = 44 P(X<44) = P(Z< +2. 0) = 0. 9772 Therefore, we conclude that 97. 72% will have a resistance less than 44 ohms. What percentage will have a resistance greater than 44 ohms? Chp. 6 Uniform and Normal EGR 252 Slide 12

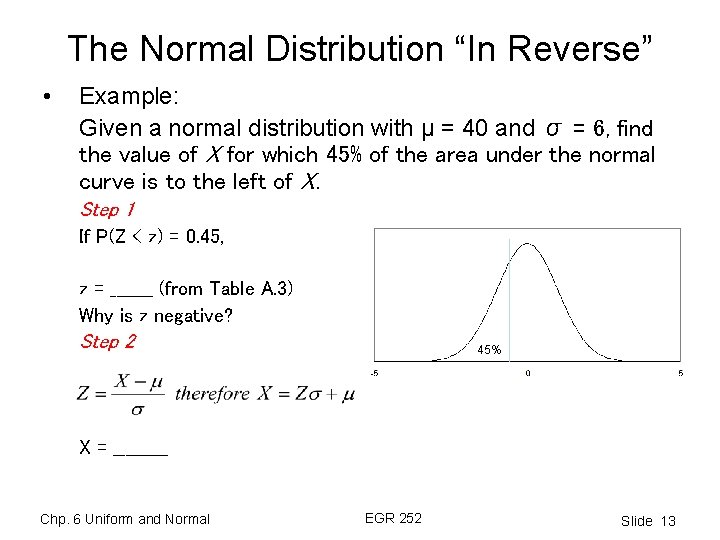
The Normal Distribution “In Reverse” • Example: Given a normal distribution with μ = 40 and σ = 6, find the value of X for which 45% of the area under the normal curve is to the left of X. Step 1 If P(Z < z) = 0. 45, z = _______ (from Table A. 3) Why is z negative? Step 2 45% X = _____ Chp. 6 Uniform and Normal EGR 252 Slide 13

In-Class Exercise 6. 14 The finished inside diameter of a piston ring is normally distributed with a mean of 10 centimeters and a standard deviation of 0. 03 centimeter. (a) What proportion of rings will have inside diameters exceeding 10. 075 centimeters? (b) What is the probability that a piston ring will have an inside diameter between 9. 97 and 10. 03 centimeters? (c) Below what value of inside diameter will 15% of the piston rings fall? of 0. 03 centimeter. Chp. 6 Uniform and Normal EGR 252 Slide 14

In-Class Exercise 6. 14 Solution (a) What proportion of rings will have inside diameters exceeding 10. 075 centimeters? (b) What is the probability that a piston ring will have an inside diameter between 9. 97 and 10. 03 centimeters? (c) Below what value of inside diameter will 15% of the piston rings fall? of 0. 03 centimeter. Chp. 6 Uniform and Normal EGR 252 Slide 15

In-Class Exercise 6. 17 The average life of a certain type of small motor is 10 years with a standard deviation of 2 years. The manufacturer replaces free all motors that fail while under guarantee. If she is willing to replace only 3% of the motors that fail, how long a guarantee should be offered? Assume that the lifetime of a motor follows a normal distribution. Chp. 6 Uniform and Normal EGR 252 Slide 16

In-Class Exercise 6. 17 The average life of a certain type of small motor is 10 years with a standard deviation of 2 years. The manufacturer replaces free all motors that fail while under guarantee. If she is willing to replace only 3% of the motors that fail, how long a guarantee should be offered? Assume that the lifetime of a motor follows a normal distribution. 3% Solve for X X = (2 * -1. 88) + 10 = 6. 24 A z-value of -1. 88 corresponds to 3% of area under the curve Chp. 6 Uniform and Normal EGR 252 Slide 17