Unified Quadratic Programming Approach for Mixed Mode Placement

Unified Quadratic Programming Approach for Mixed Mode Placement Bo Yao, Hongyu Chen, Chung-Kuan Cheng, Nan-Chi Chou*, Lung-Tien Liu*, Peter Suaris* CSE Department University of California, San Diego *Mentor Graphics Corporation

Outline Introduction to the mixed mode placement Unified cost function DCT based cell density cost Experimental results Conclusions

Mixed Mode Placement Common design needs n n Mixed signal designs (analog and RF parts are macros) Hierarchical design style IP blocks Memory blocks Challenges for placement n n Huge amount of components Heterogeneous module sizes/shapes IP Memory Analog

Previous Works on Mixed Mode Placement Combined floorplanning and std. cell placement n Capo (Markov, ISPD 02, ICCAD 2003) Multi-level annealing placement n m. PG-MS (Cong, ASPDAC 2003) Partitioning based approaches n Feng Shui (Madden, ISPD 04) Force-directed / analytical approaches n Kraftwork (Eisenmann and Johannas, DAC 98 ) n Fast. Place (Chu, ISPD 04) APlace (Kahng, ISPD 04, ICCAD 04) n

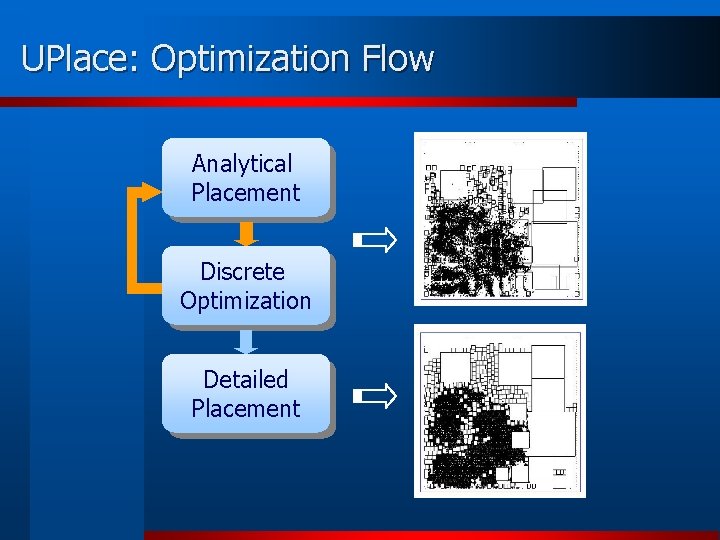
UPlace: Optimization Flow Analytical Placement Discrete Optimization Detailed Placement

Unified Cost Function Combined object function for global placement n n DP: Penalties for un-even cell densities WL: Wire length cost function n Quadratic analytical placement WL = 1/2 x. TQx+px +1/2 y. TQy+py n Bounding box wire length for discrete optimization

Cell Density Common strategy n Partition the placement area into N by N rooms Cell density matrix D = {dij} n dij is the total cell area in room (i, j) A

DCT: Cell Density in Frequency Domain 2 -D Discrete Cosine Transform (DCT) Cell density matrix D => Frequency matrix F = {fij} where fij is the weight of density pattern (i, j)

Properties of Frequency Matrix Each fuv is the weight of frequency (u, v) … (0, 0) Inverse DCT recovers the cell density (1, 0) (3, 0) … (0, 1) … (1, 1) … (0, 3) (3, 3)

Frequency Matrix: An Example Density matrix D and frequency matrix F … (0, 0) (1, 0) (3, 0) … (0, 1) … (1, 1) … (0, 3) (3, 3)

Properties of DCT Cell density energy dij 2 = fij 2 Cell perturbation and frequency matrix Uniform density fij = 0

Density Cost of a Placement Weighted sum of fij 2 Higher weight for lower frequency

Approximation of the Density Cost Approximate the density cost with a quadratic function DP = ½aixi 2+ bixi+ci DP Make DP convex n xi ai >= 0 to ensure Matrix form x- x DP = ½x. TAx+Bx DP x+ A = diag(a 1, a 2, …, an), xi B=(b 1, b 2, …, bn)T x- x ai > 0 x+ ai = 0

UPlace: Minimize Combined Objective Function Combine quadratic objectives n n n WL + DP WL = ½ x. TQx+px DP = ½x. TAx+Bx Solve linear equation for each minimization n (Q + A)x = -p - B Use Lagrange relaxation to reduce cell congestion n (k+1) = (k) + (k)* DP n 0 = 0, 0 = Const n (k+1) = (k) * , 0< 1

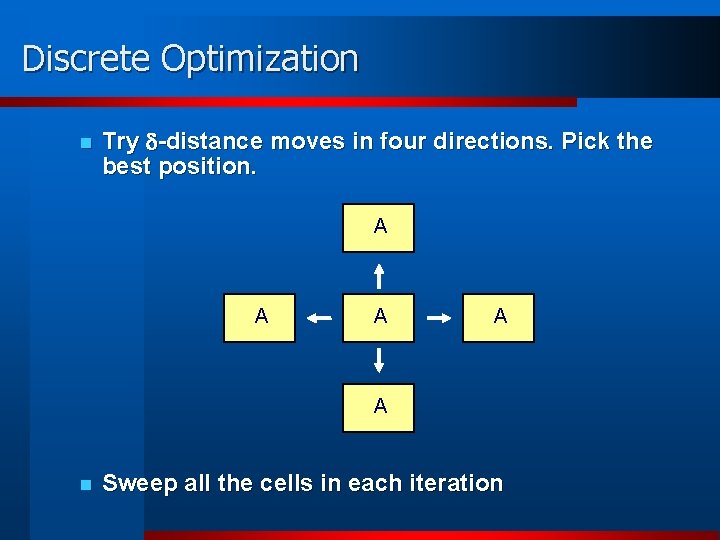
Discrete Optimization n Try -distance moves in four directions. Pick the best position. A A A n Sweep all the cells in each iteration

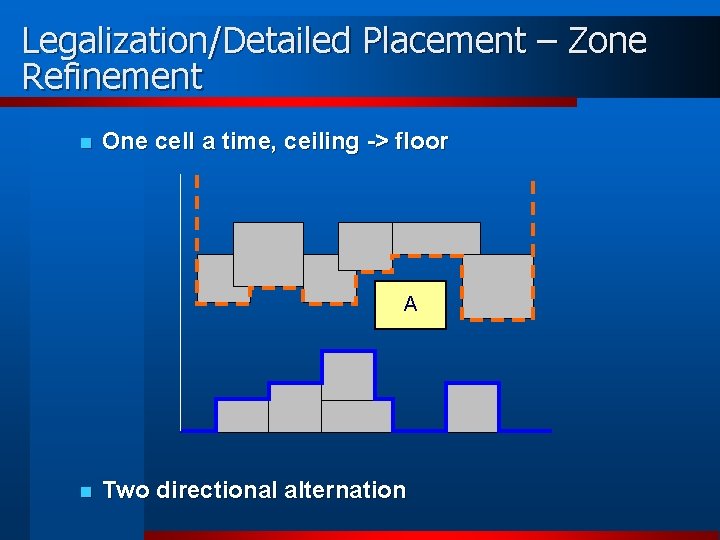
Legalization/Detailed Placement – Zone Refinement n One cell a time, ceiling -> floor A n Two directional alternation

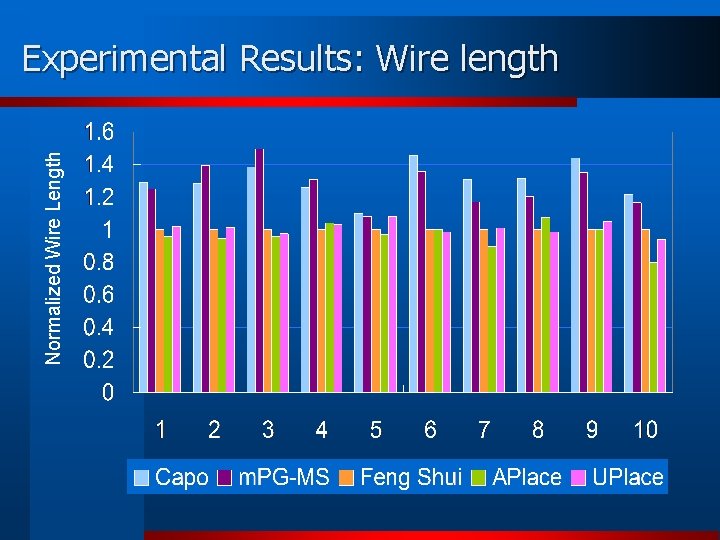
Normalized Wire Length Experimental Results: Wire length

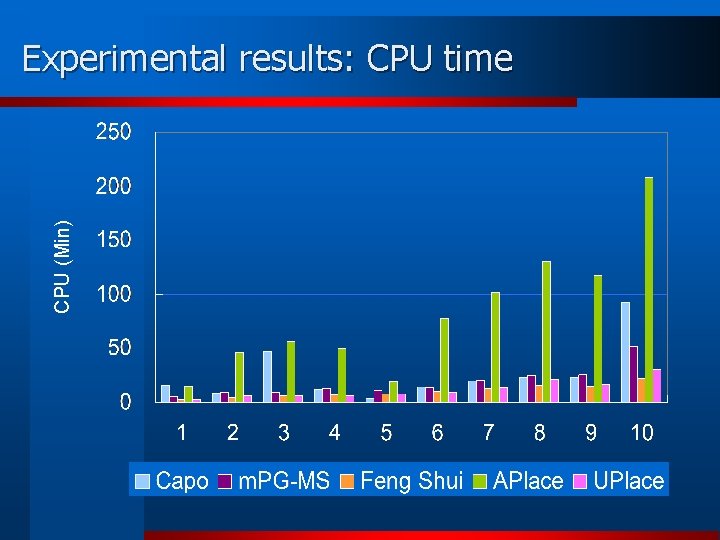
CPU (Min) Experimental results: CPU time

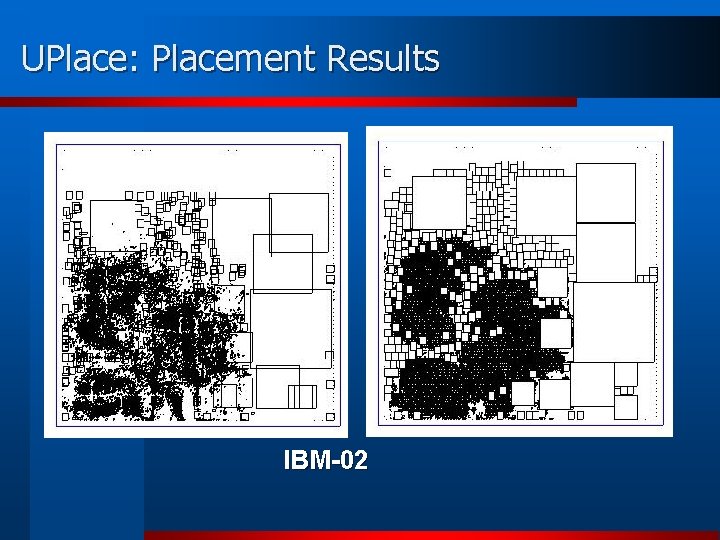
UPlace: Placement Results IBM-02

Conclusions We propose a unified cost function for global optimization, which provides good trade-offs between wire length minimization and cell spreading. We introduce a DCT based cell density calculation method, and a quadratic approximation. The unified placement approach generates promising results on mixed mode designs.

Thank You !