Unified Description of Bound and Unbound States Resolution

Unified Description of Bound and Unbound States -- Resolution of Identity -KEK Lecture (2) K. Kato Hokkaido University Oct. 6, 2010

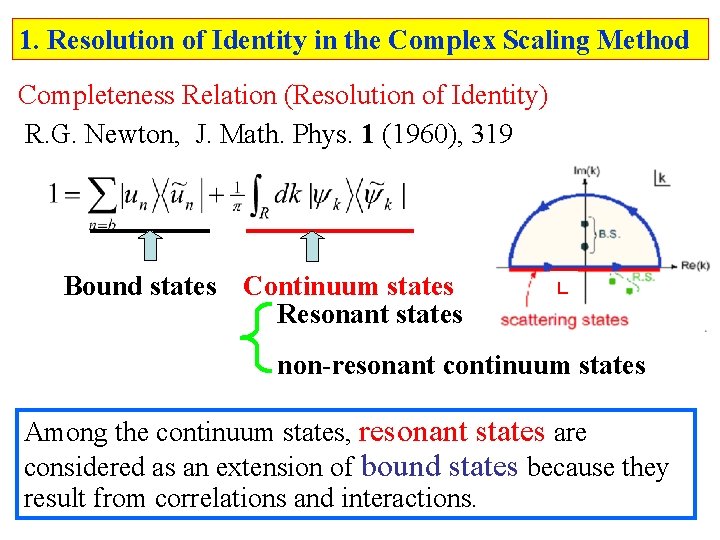
1. Resolution of Identity in the Complex Scaling Method Completeness Relation (Resolution of Identity) R. G. Newton, J. Math. Phys. 1 (1960), 319 Bound states Continuum states Resonant states Ｌ non-resonant continuum states Among the continuum states, resonant states are considered as an extension of bound states because they result from correlations and interactions.

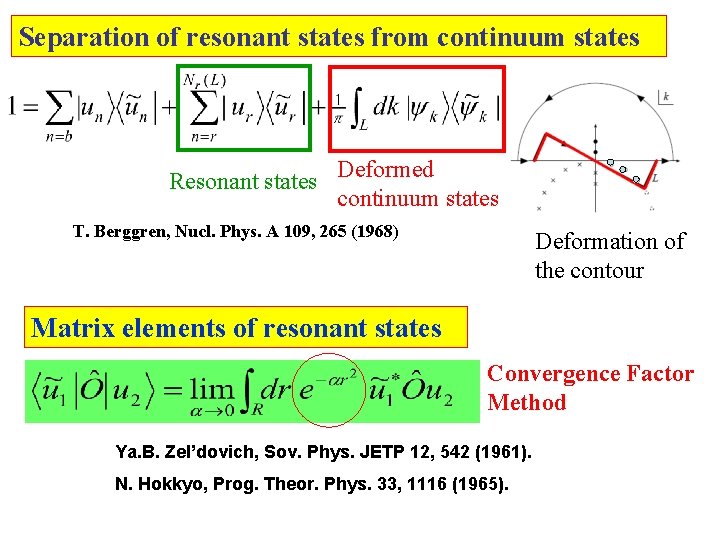
Separation of resonant states from continuum states Resonant states Deformed continuum states T. Berggren, Nucl. Phys. A 109, 265 (1968) Deformation of the contour Matrix elements of resonant states Convergence Factor Method Ya. B. Zel’dovich, Sov. Phys. JETP 12, 542 (1961). N. Hokkyo, Prog. Theor. Phys. 33, 1116 (1965).

Complex scaling method coordinate: J. Aguilar and J. M. Combes, J. Math. Phys. 22, 269 (1971) E. Balslev and J. M. Combes, J. Math. Phys. 22, 280 (1971) reiθ r B. Gyarmati and T. Vertse, Nucl. Phys. A 160, 523 (1971). momentum: T. Myo, A. Ohnishi and K. Kato. Prog. Theor. Phys. 99(1998)801] Resonant states Rotated Continuum states

Resolution of Identity in Complex Scaling Method k E k Single Channel system E B. Giraud and K. Kato, Ann. of Phys. 308 (2003), 115.

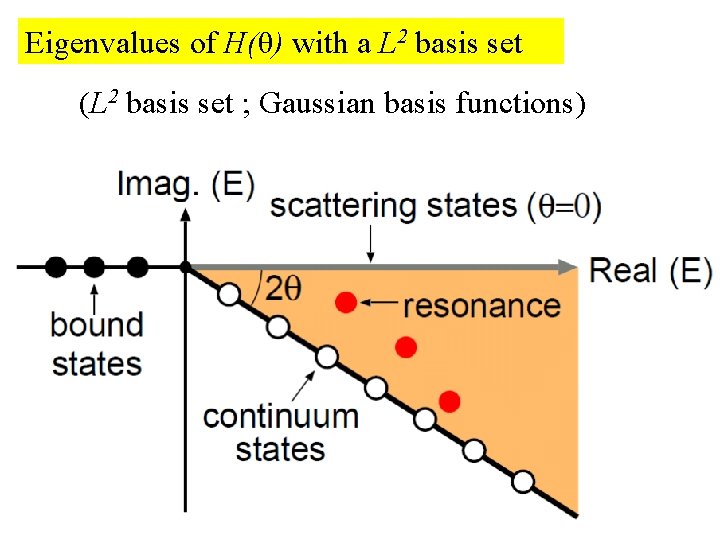
Eigenvalues of H(θ) with a L 2 basis set (L 2 basis set ; Gaussian basis functions)

E| E| b 3 b 2 b 1 r 2 r 3 B. Giraud, K. Kato and A. Ohnishi, J. of Phys. A 37 (2004), 11575 Coupled Channel system Bany-body system Three-body system

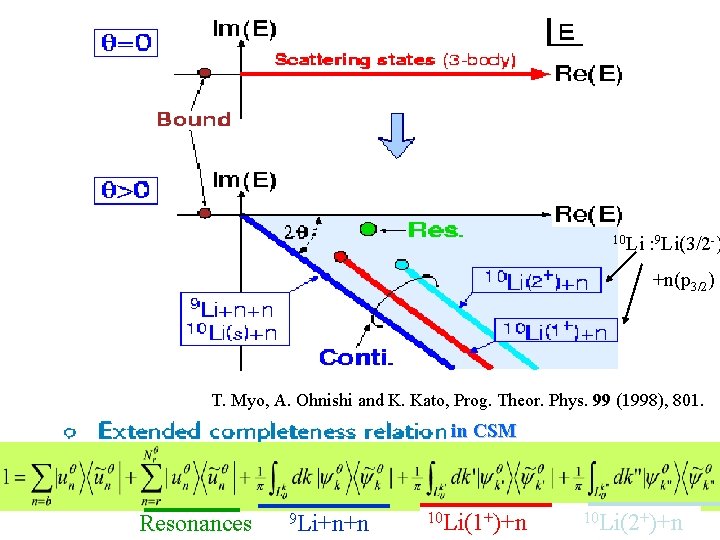
10 Li : 9 Li(3/2 -) +n(p 3/2) T. Myo, A. Ohnishi and K. Kato, Prog. Theor. Phys. 99 (1998), 801. in CSM Resonances 9 Li+n+n 10 Li(1+)+n 10 Li(2+)+n

Complex Scaled Green’s Functions Green’s operator Complex scaled Green’s operator Resolution of Identity Complex Scaled Green’s function

2. Strength Functions and Coulomb Breakup Reaction

Coulomb Breakup Reactions of Three-Body Systems (twoneutron halo systems) Neutron-correlation in 2 -neutron halo states Simultaneous description of Structure and Reaction Breakup Mechanism: Direct or Sequential ?

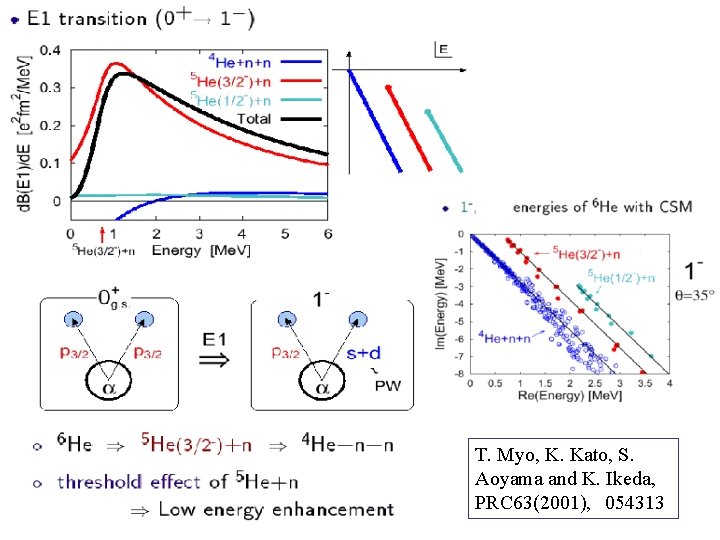
T. Myo, K. Kato, S. Aoyama and K. Ikeda, PRC 63(2001), 　054313

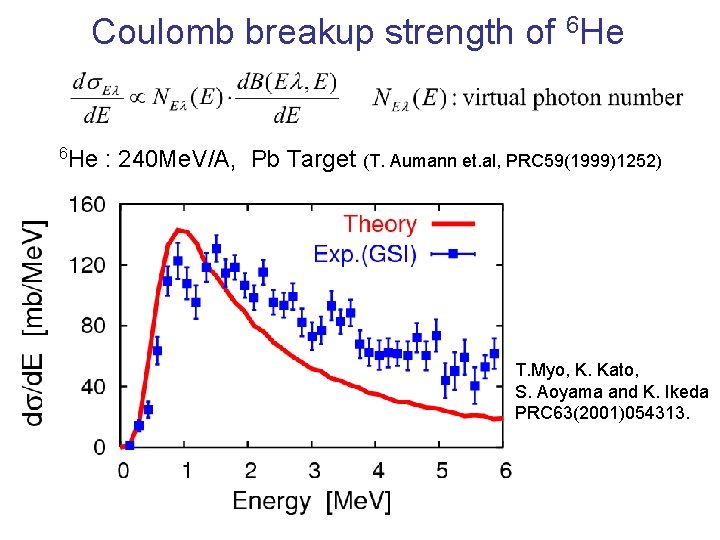
Coulomb breakup strength of 6 He : 240 Me. V/A, Pb Target (T. Aumann et. al, PRC 59(1999)1252) T. Myo, K. Kato, S. Aoyama and K. Ikeda PRC 63(2001)054313.

Coulomb breakup cross section of 11 Li T. Nakamura et al. , Phys. Rev. Lett. 96, 252502 (2006)

3. Continuum level density Definition of LD: A. T. Kruppa, Phys. Lett. B 431 (1998), 237 -241 A. T. Kruppa and K. Arai, Phys. Rev. A 59 (1999), 2556 K. Arai and A. T. Kruppa, Phys. Rev. C 60 (1999) 064315

1 RI in complex scaling Resonance: Continuum: Discreet distribution

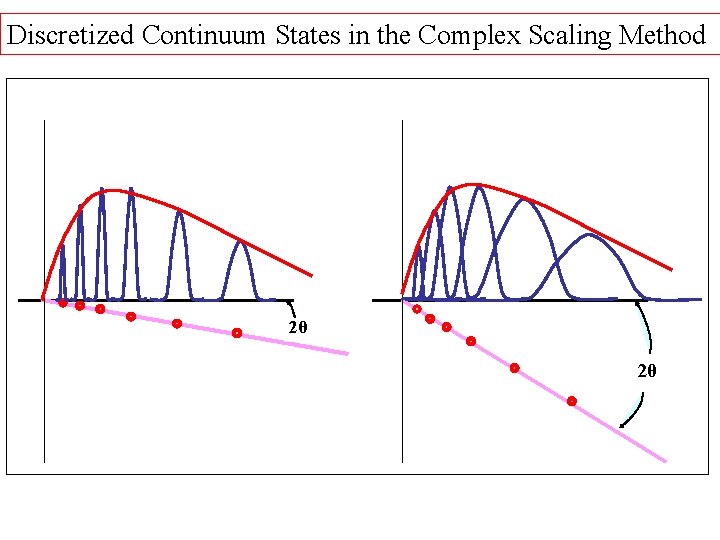
Discretized Continuum States in the Complex Scaling Method εI εI E E 2θ 2θ

Continuum Level Density: Basis function method:

Phase shift calculation in the complex scaled basis function method S. Shlomo, Nucl. Phys. A 539 (1992), 17. In a single channel case,

Phase shift of 8 Be= + calculated with discretized app. Base+CSM: 30 Gaussian basis and =20 deg.

Continuum Level Density of 3α system [Ref. ] S. Shlomo, NPA 539 (1992) 17. 8 Be α１ α２ • α 1 - α 2: resonance + continuum • (α 1α 2)- α 3: continuum α３ • α 1 - α 2: continuum • (α 1α 2)- α 3: continuum

Continuum Level 02 + 03 + (2 +) 04 + 05 +

4. Complex scaled Lippmann-Schwinger equation H 0=T+VC V；　Short Range Interaction （Ψ 0; regular at origin） Solutions of Lippmann-Schwinger Equation Outgoing waves Complex Scaling A. Kruppa, R. Suzuki and K. Kato, phys. Rev. C 75 (2007), 044602

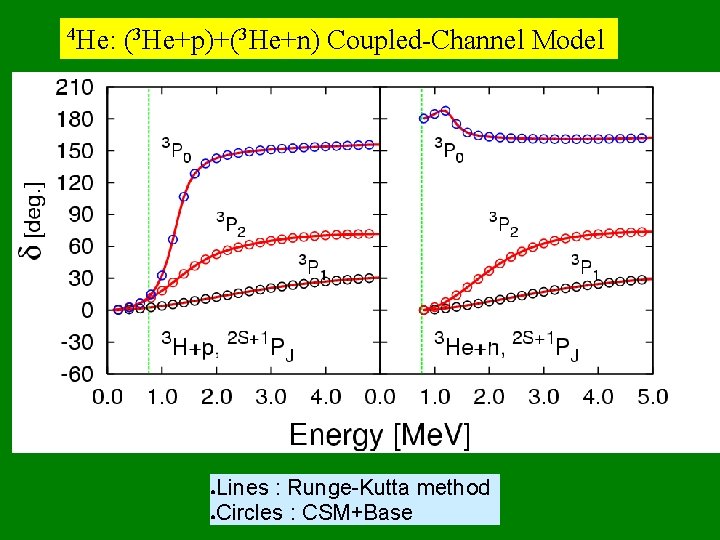
4 He: (3 He+p)+(3 He+n) Coupled-Channel Model Lines : Runge-Kutta method ●Circles : CSM+Base ●

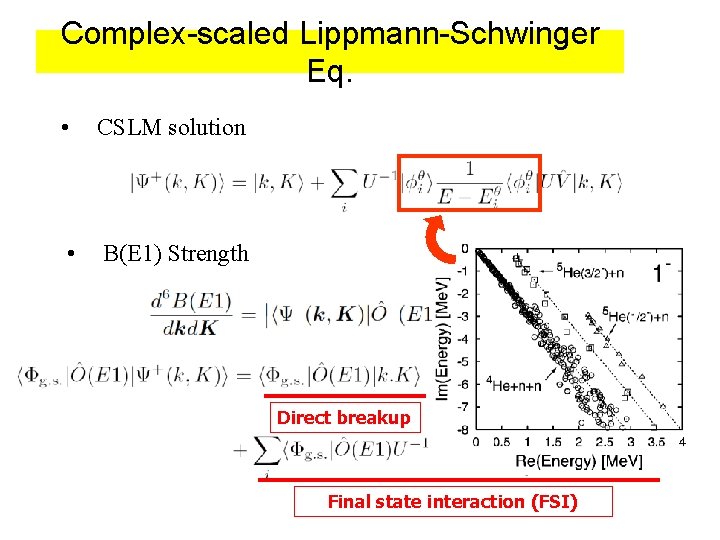
Complex-scaled Lippmann-Schwinger Eq. • CSLM solution • B(E 1) Strength Direct breakup Final state interaction (FSI)

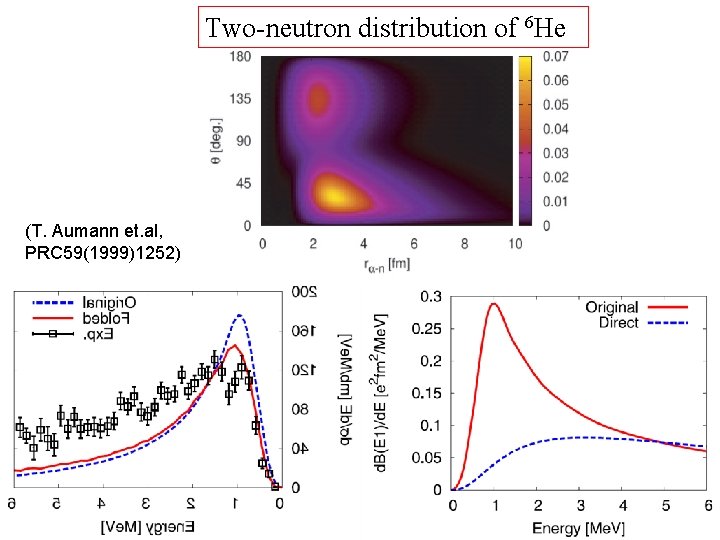
Two-neutron distribution of 6 He (T. Aumann et. al, PRC 59(1999)1252)

(T. Aumann et. al, PRC 59(1999)1252)

Summary and conclusion • The resolution of identity in the complex scaling method is presented to treat the resonant states in the same way as bound states. • The complex scaling method is shown to describe not only resonant states but also continuum states on the rotated branch cuts. • We presented several applications of the extended resolution of identity in the complex scaling method; strength functions of the Coulomb break reactions, continuum level density and three-body scattering states. • Many-body resonant states of He-isotopes are studied.

Collaborators Y. Kikuchi, K. Yamamoto, A. Wano, T. Myo, M. Takashina, C. Kurokawa, R. Suzuki, K. Arai, H. Masui, S. Aoyama, K. Ikeda, A. Kruppa. B. Giraud