Unification Forward Chaining Backward Chaining 1 premise inference

• Unification (統一) • Forward Chaining (前向き推論) • Backward Chaining (後ろ向き推論) 1

premise inference Inference engine substitution match unify interaction attempt prove conclusion consequence

Seven inference rules for propositional Logic • R(1) Modus Ponens , • R(2) And-Elimination 1 2 … n • R(3) And-Introduction 1, 2, …, n 1 2 … n • R(4) Or-Introduction i 1 2 … n i • R(5) Double-Negation Elimination • R(6) Unit Resolution , • R(7) Logic connectives: , 3

The three new inference rules • R (8) Universal Elimination: For any sentence , variable v, and ground term g: v Ground term is a term that contains no variables. SUBST({v/g}, ) e. g. , x Likes(x, Ice. Cream), we can use the substitute {x/Rose} and infer Like(Rose, Ice. Cream). • R (9) Existential Elimination: For any sentence , variable v, and constant symbol k that does not appear elsewhere in the knowledge base: v SUBST({v/k}, ) e. g. , x Kill(x, Victim), we can infer Kill(Murderer, Victim), as long as Murderer does not appear elsewhere in the knowledge base. • R (10) Existential Introduction: For any sentence , variable v that does not occur in , and ground term g that does occur in : e. g. , from Likes(Rose, Ice. Cream) we can infer x Likes(x, Ice. Cream). v SUBST({g/v}, ) 4

Example of proof (証明) Bob is a buffalo | 1. Buffalo(Bob) --f 1 Pat is a pig | 2. Pig(Pat) --f 2 Buffaloes run faster than pigs | 3. x, y Buffalo(x) Pig(y) Faster(x, y) --r 1 --------------------------------------------------To proof: Bob runs faster than Pat -------------------------------------------------Apply R(3) to f 1 And f 2 | 4. Buffalo(Bob) Pig(Pat) --f 3 (And-Introduction) Apply R(8) to r 1 {x/Bob, y/Pat} | 5. Buffalo(Bob) Pig(Pat) Faster(Bob, Pat) --f 4 (Universal-Elimination) Apply R(1) to f 3 And f 4 (Inplication-Elimination ) | 6. Faster(Bob, Pat) --f 5 5

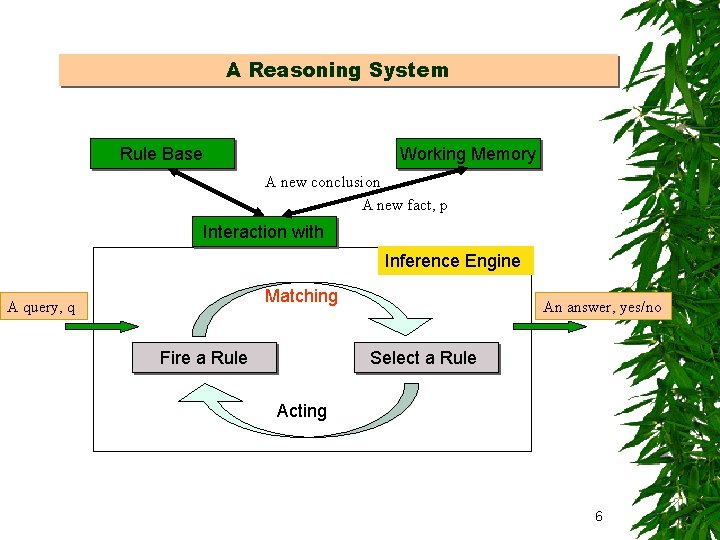
A Reasoning System Rule Base Working Memory A new conclusion A new fact, p Interaction with Inference Engine Matching A query, q Fire a Rule An answer, yes/no Select a Rule Acting 6

Unify Unification function, Unify, is to take two atomic sentences p and q and return a substitution that would make p and q look the same. A substitute unifies atomic sentences p and q if p =q For example, p q ------------------------------------------------------------------------------------------------------- Knows(John, x) | Knows(John, Jane) | Knows(y, OJ) | Knows(y, Mother(y)) | {x/Jane} | {y/John, x/OJ} | {y/John, x/Mother(John)} Premise 前提 7

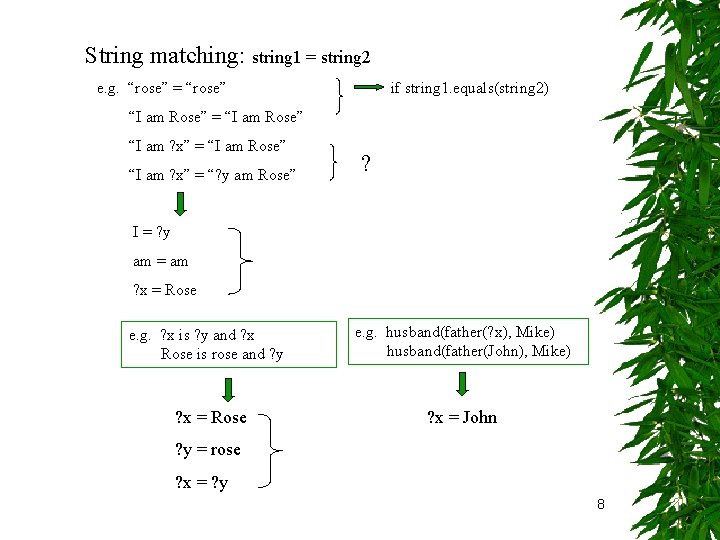
String matching: string 1 = string 2 e. g. “rose” = “rose” if string 1. equals(string 2) “I am Rose” = “I am Rose” “I am ? x” = “? y am Rose” ? I = ? y am = am ? x = Rose e. g. ? x is ? y and ? x Rose is rose and ? y e. g. husband(father(? x), Mike) husband(father(John), Mike) ? x = Rose ? x = John ? y = rose ? x = ? y 8

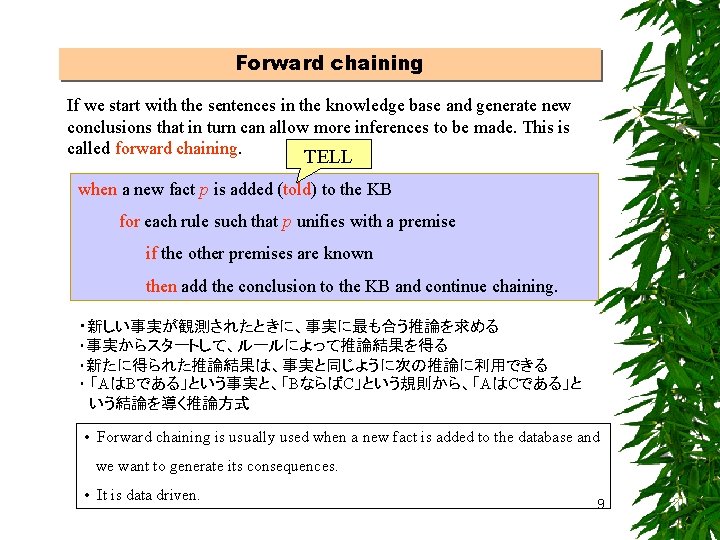
Forward chaining If we start with the sentences in the knowledge base and generate new conclusions that in turn can allow more inferences to be made. This is called forward chaining. TELL when a new fact p is added (told) to the KB for each rule such that p unifies with a premise if the other premises are known then add the conclusion to the KB and continue chaining. ・新しい事実が観測されたときに、事実に最も合う推論を求める ・事実からスタートして、ルールによって推論結果を得る ・新たに得られた推論結果は、事実と同じように次の推論に利用できる ・ 「AはBである」という事実と、「BならばC」という規則から、「AはCである」と 　いう結論を導く推論方式 • Forward chaining is usually used when a new fact is added to the database and we want to generate its consequences. • It is data driven. 9

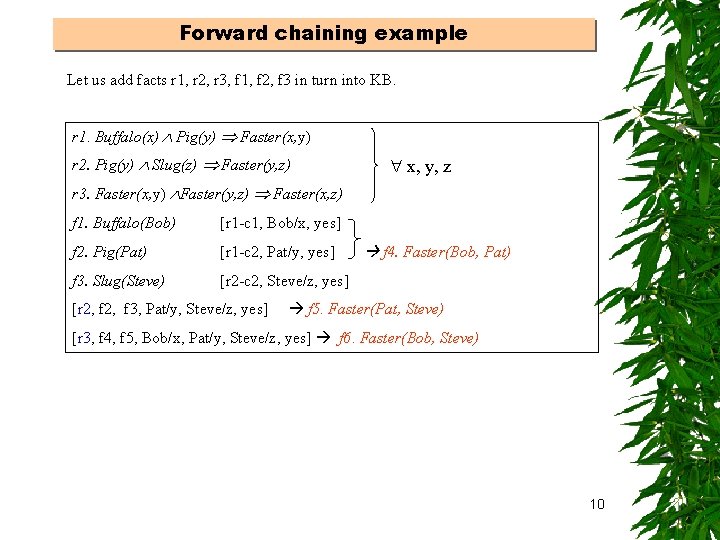
Forward chaining example Let us add facts r 1, r 2, r 3, f 1, f 2, f 3 in turn into KB. r 1. Buffalo(x) Pig(y) Faster(x, y) r 2. Pig(y) Slug(z) Faster(y, z) x, y, z r 3. Faster(x, y) Faster(y, z) Faster(x, z) f 1. Buffalo(Bob) [r 1 -c 1, Bob/x, yes] f 2. Pig(Pat) [r 1 -c 2, Pat/y, yes] f 3. Slug(Steve) [r 2 -c 2, Steve/z, yes] [r 2, f 3, Pat/y, Steve/z, yes] f 4. Faster(Bob, Pat) f 5. Faster(Pat, Steve) [r 3, f 4, f 5, Bob/x, Pat/y, Steve/z, yes] f 6. Faster(Bob, Steve) 10

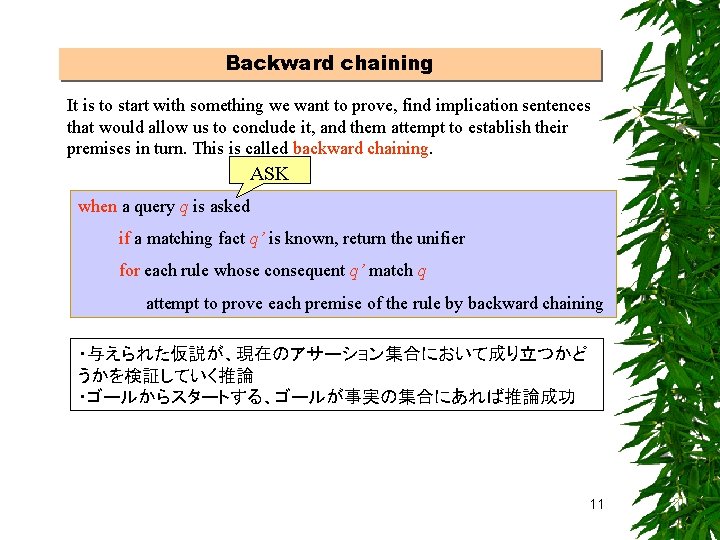
Backward chaining It is to start with something we want to prove, find implication sentences that would allow us to conclude it, and them attempt to establish their premises in turn. This is called backward chaining. ASK when a query q is asked if a matching fact q’ is known, return the unifier for each rule whose consequent q’ match q attempt to prove each premise of the rule by backward chaining ・与えられた仮説が、現在のアサーション集合において成り立つかど うかを検証していく推論 ・ゴールからスタートする、ゴールが事実の集合にあれば推論成功 11

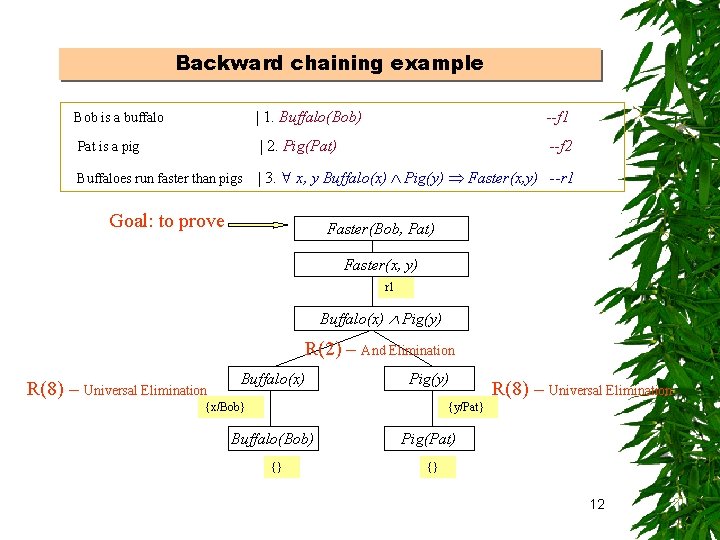
Backward chaining example Bob is a buffalo | 1. Buffalo(Bob) --f 1 Pat is a pig | 2. Pig(Pat) --f 2 Buffaloes run faster than pigs | 3. x, y Buffalo(x) Pig(y) Faster(x, y) --r 1 Goal: to prove Faster(Bob, Pat) Faster(x, y) r 1 Buffalo(x) Pig(y) R(2) – And Elimination R(8) – Universal Elimination Buffalo(x) Pig(y) {x/Bob} R(8) – Universal Elimination {y/Pat} Buffalo(Bob) {} Pig(Pat) {} 12

Rules defined in the rule base file: Car. Shop rule if then rule if "Car. Rule 1" "? x is inexpensive" "? x is made in Japan" "Car. Rule 2" "? x is small" "? x is made in Japan" "Car. Rule 3" "? x is expensive" "? x is a foreign car" "Car. Rule 4" "? x is big" "? x needs a lot of gas" then "? x is a foreign car" rule "Car. Rule 5" if "? x is made in Japan" "? x has Toyota's logo" then "? x is a Toyota" rule "Car. Rule 6" if "? x is made in Japan" "? x is a popular car" then "? x is a Toyota" rule "Car. Rule 7" if "? x is made in Japan" "? x has Honda's logo" then "? x is a Honda" rule "Car. Rule 8" if "? x is made in Japan" "? x has a VTEC engine" then "? x is a Honda" rule "Car. Rule 9“ if "? x is a Toyota" "? x has several seats" "? x is a wagon" then "? x is a Carolla Wagon" rule "Car. Rule 10" if "? x is a Toyota" "? x has several seats" "? x is a hybrid car" then "? x is a Prius" rule "Car. Rule 11" if "? x is a Honda" "? x is stylish" "? x has several color models" "? x has several seats" "? x is a wagon" then "? x is an Accord Wagon" rule "Car. Rule 12" if "? x is a Honda" "? x has an aluminium body" "? x has only 2 seats" then "? x is a NSX" rule "Car. Rule 13" if "? x is a foreign car" "? x is a sports car" "? x is stylish" "? x has several color models" "? x has a big engine" then "? x is a Lamborghini Countach" rule "Car. Rule 14" if "? x is a foreign car" "? x is a sports car" "? x is red" "? x has a big engine" then "? x is a Ferrari F 50" rule "Car. Rule 15" if "? x is a foreign car" "? x is a good face" then "? x is a Jaguar XJ 8"

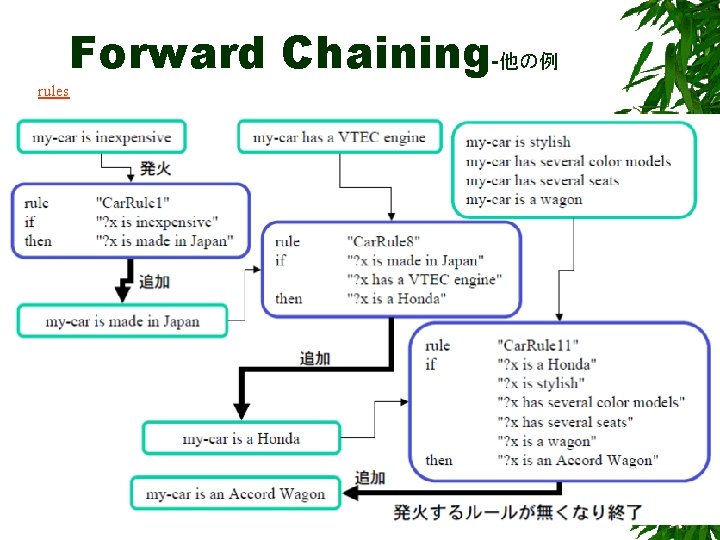
Forward Chaining-他の例 rules 14

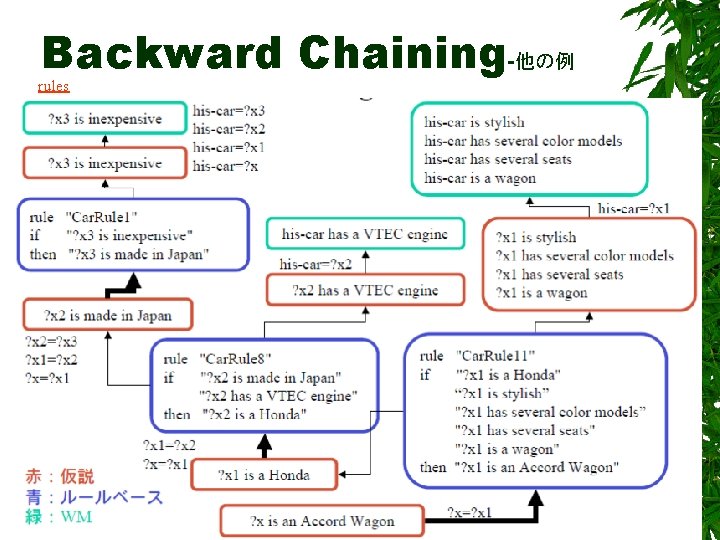
Backward Chaining-他の例 rules 15

forward/backward chaining demo agent. Soft/ciagent/part 1/rule/Rule. Applet. html Working memory Vehicle Rule Base Vehicles Rule Base: bicycle: IF vehicle. Type=cycle sedan: IF vehicle. Type=automobile vehicle. Type value = null AND size=medium size value = null AND num_wheels=2 AND num_doors=4 num_wheels value = null AND motor=no THEN vehicle=Sedan num_doors value = null THEN vehicle=Bicycle tricycle: IF vehicle. Type=cycle mini. Van: IF vehicle. Type=automobile motor value = null AND size=medium vehicle value = null AND num_wheels=3 AND num_doors=3 vehicle. Type value = null AND motor=no THEN vehicle=Mini. Van size value = null THEN vehicle=Tricycle motorcycle: IF vehicle. Type=cycle AND num_wheels=2 AND motor=yes THEN vehicle=Motorcycle sports. Car: IF vehicle. Type=automobile AND size=small AND num_doors=2 THEN vehicle=Sports_Car SUV: IF vehicle. Type=automobile num_wheels value = null AND size=large num_doors value = null AND num_doors=4 motor value = null THEN vehicle=Sports_Utility_Vehicle Cycle: IF num_wheels<4 THEN vehicle. Type=cycle Automobile: IF num_wheels=4 vehicle value = null size set to medium num_wheels set to 4 motor set to yes num_doors set to 3 AND motor=yes THEN vehicle. Type=automobile 16

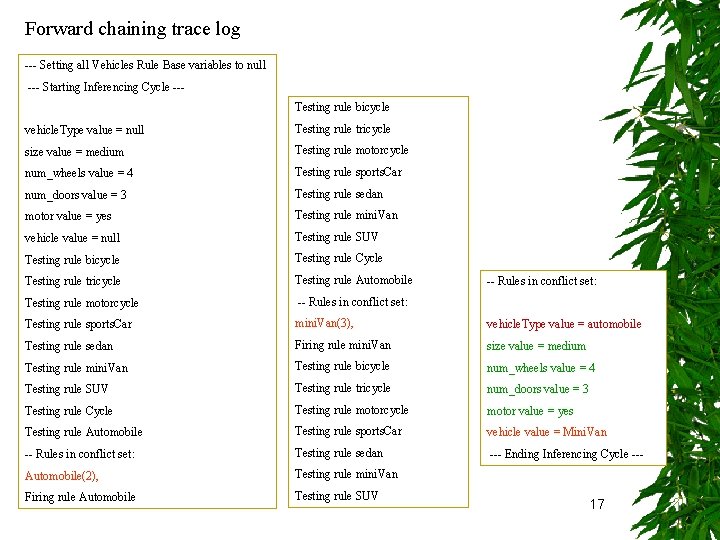
Forward chaining trace log --- Setting all Vehicles Rule Base variables to null --- Starting Inferencing Cycle --Testing rule bicycle vehicle. Type value = null Testing rule tricycle size value = medium Testing rule motorcycle num_wheels value = 4 Testing rule sports. Car num_doors value = 3 Testing rule sedan motor value = yes Testing rule mini. Van vehicle value = null Testing rule SUV Testing rule bicycle Testing rule Cycle Testing rule tricycle Testing rule Automobile Testing rule motorcycle -- Rules in conflict set: Testing rule sports. Car mini. Van(3), vehicle. Type value = automobile Testing rule sedan Firing rule mini. Van size value = medium Testing rule mini. Van Testing rule bicycle num_wheels value = 4 Testing rule SUV Testing rule tricycle num_doors value = 3 Testing rule Cycle Testing rule motorcycle motor value = yes Testing rule Automobile Testing rule sports. Car vehicle value = Mini. Van -- Rules in conflict set: Testing rule sedan --- Ending Inferencing Cycle --- Automobile(2), Testing rule mini. Van Firing rule Automobile Testing rule SUV -- Rules in conflict set: 17

Backward chaining trace log The goal is set as Mini. Van Evaluating rule motorcycle --- Starting Demo Backward. Chain --- Rule motorcycle is false, can't set vehicle Evaluating rule sports. Car vehicle. Type value = null Rule sports. Car is false, can't set vehicle size value = medium Evaluating rule sedan num_wheels value = 4 Rule sedan is false, can't set vehicle num_doors value = 3 Evaluating rule mini. Van motor value = yes Rule mini. Van is true, setting vehicle: = Mini. Van vehicle value = null +++ Found Solution for goal: vehicle Evaluating rule bicycle --- Stopping Demo Backward. Chain! --- Evaluating rule Cycle Rule Cycle is false, can't set vehicle. Type value = automobile Evaluating rule Automobile size value = medium Rule Automobile is true, setting vehicle. Type: = automobile num_wheels value = 4 Rule bicycle is false, can't set vehicle num_doors value = 3 Evaluating rule tricycle motor value = yes Rule tricycle is false, can't set vehicle value = Mini. Van 18

Quiz: Understand the forward chaining algorithm and think an example. Home Work: Understand the backward chaining algorithms and think an example. 19