UNIDADES DE MEDIDA DEL MOVIMIENTO VECTORES Y MOVIMIENTO

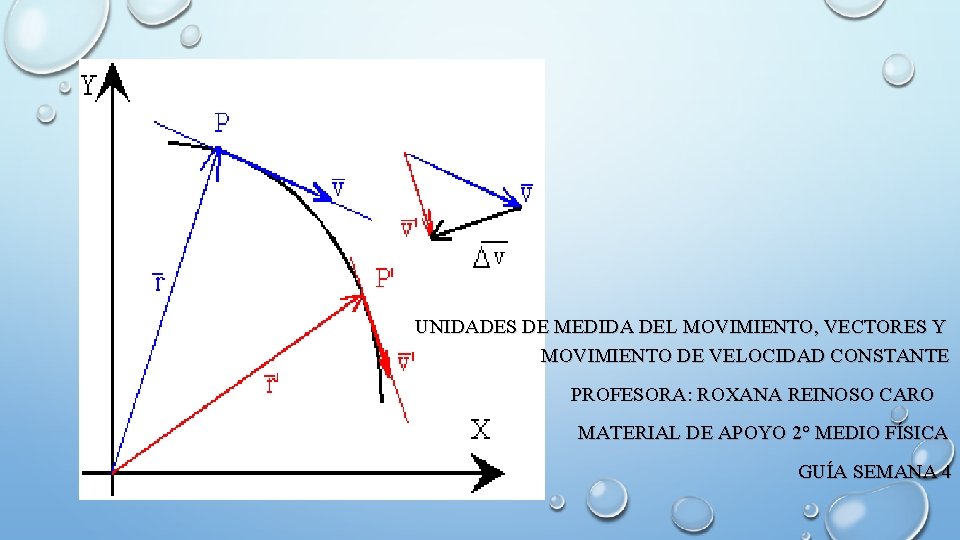
UNIDADES DE MEDIDA DEL MOVIMIENTO, VECTORES Y MOVIMIENTO DE VELOCIDAD CONSTANTE PROFESORA: ROXANA REINOSO CARO MATERIAL DE APOYO 2° MEDIO FÍSICA GUÍA SEMANA 4

Aprendizajes esperados • • • Transformar unidades. Despejar ecuaciones básicas. Conocer las características principales de un gráfico. Conocer las coordenadas cartesianas y realizar un gráfico con estas. Analizar los gráficos lineales y cuadráticos. Reconocer las magnitudes escalares. Reconocer las magnitudes vectoriales. Aplicar operaciones entre vectores. Caracterizar el movimiento rectilíneo uniforme (MRU). Interpretar información en gráficos.

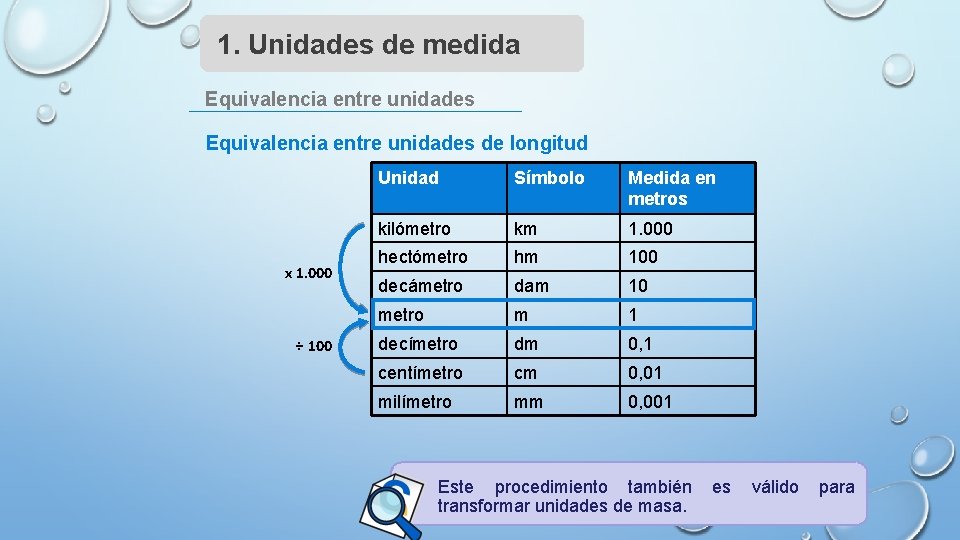
1. Unidades de medida Equivalencia entre unidades de longitud x 1. 000 ÷ 100 Unidad Símbolo Medida en metros kilómetro km 1. 000 hectómetro hm 100 decámetro dam 10 metro m 1 decímetro dm 0, 1 centímetro cm 0, 01 milímetro mm 0, 001 Este procedimiento también transformar unidades de masa. es válido para

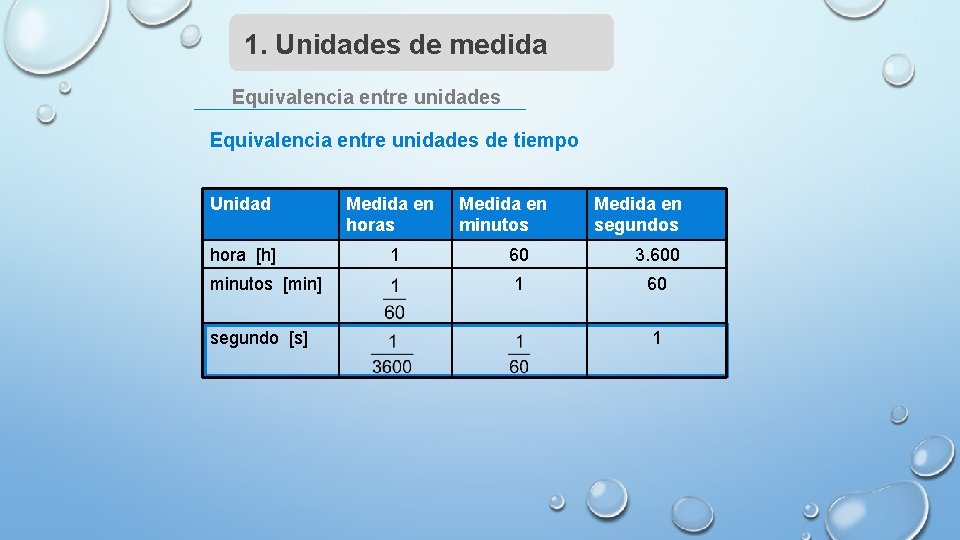
1. Unidades de medida Equivalencia entre unidades de tiempo Unidad Medida en horas hora [h] 1 minutos [min] segundo [s] Medida en minutos Medida en segundos 60 3. 600 1 60 1

1. Unidades de medida Equivalencia entre unidades Una conversión muy útil Si necesitamos pasar desde a o viceversa, podemos seguir este sencillo procedimiento. x 3, 6 ÷ 3, 6

2. Resolución de ecuaciones simples Ecuación: Igualdad en la que intervienen uno o más términos, llamados incógnitas. Es decir, es una igualdad entre expresiones algebraicas.

3. Gráficos Representación gráfica Por ejemplo, grafiquemos la información del siguiente cuadro: Primero, asignamos las variables a cada eje: t : tiempo en [s] (asociado al eje de las abscisas) d : distancia en [m] (asociado al eje de las ordenadas) d[m] t [segundos] d [metros] 0 0 3 1 6 2 9 3 3 2 Eje vertical, eje de las ordenadas. Eje horizontal, eje de las abscisas. 1 0 3 6 9 t[s]

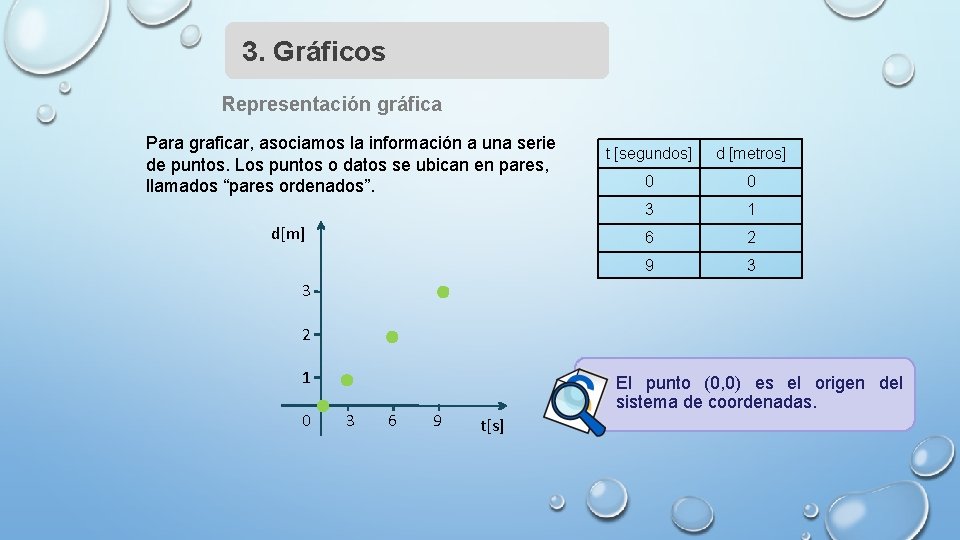
3. Gráficos Representación gráfica Para graficar, asociamos la información a una serie de puntos. Los puntos o datos se ubican en pares, llamados “pares ordenados”. d[m] t [segundos] d [metros] 0 0 3 1 6 2 9 3 3 2 1 0 3 6 9 El punto (0, 0) es el origen del sistema de coordenadas. t[s]

3. Gráficos Representación gráfica Finalmente, unimos todos los puntos con una línea, que puede ser recta o curva, dependiendo de la relación que exista entre las variables graficadas. En este caso, es una recta. En la práctica, basta dibujar unos pocos puntos y unirlos convenientemente para obtener, con una buena aproximación, el gráfico. d[m] De la información entregada en el gráfico se ve que, por cada 3 segundos, el móvil avanza 1 metro; es decir, la relación entre las variables es muy “ordenada”. Esta relación es representada en el gráfico por una línea recta. Este tipo de gráficos recibe el nombre de “gráfico lineal” 3 2 1 0 3 6 9 t[s]

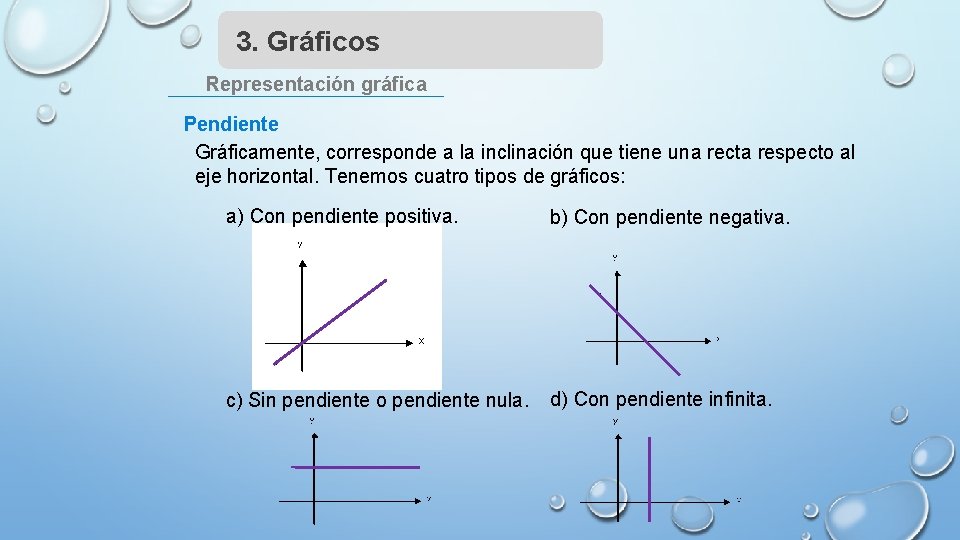
3. Gráficos Representación gráfica Pendiente Gráficamente, corresponde a la inclinación que tiene una recta respecto al eje horizontal. Tenemos cuatro tipos de gráficos: a) Con pendiente positiva. b) Con pendiente negativa. c) Sin pendiente o pendiente nula. d) Con pendiente infinita.

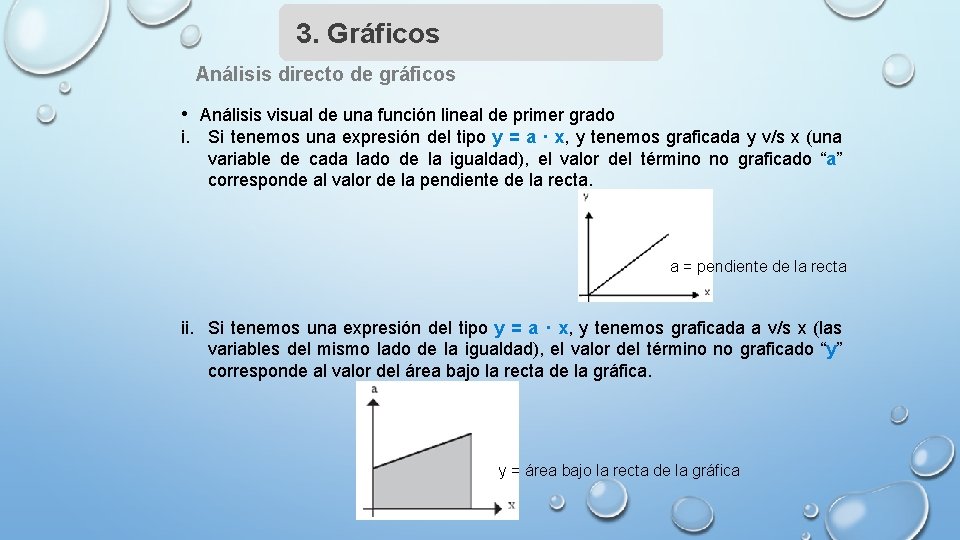
3. Gráficos Análisis directo de gráficos • Análisis visual de una función lineal de primer grado i. Si tenemos una expresión del tipo y = a · x, y tenemos graficada y v/s x (una variable de cada lado de la igualdad), el valor del término no graficado “a” corresponde al valor de la pendiente de la recta. a = pendiente de la recta ii. Si tenemos una expresión del tipo y = a · x, y tenemos graficada a v/s x (las variables del mismo lado de la igualdad), el valor del término no graficado “y” corresponde al valor del área bajo la recta de la gráfica. y = área bajo la recta de la gráfica

3. Gráficos Análisis directo de gráficos Si la función tiene término independiente, o sea, si es de la forma y = ax + b donde a y b son constantes, su intercepto sobre el eje de las “y” es igual al término independiente b (coeficiente de posición) y el termino “a”, que acompaña a la variable “x”, representa el valor de la pendiente. Por ejemplo: Sea TK : temperatura kelvin TC : temperatura Celsius Si la ecuación que vincula ambas temperaturas es TK = TC + 273, entonces, ¿cuál es el gráfico que representa mejor esta relación? TK = TC + 273 → ec. de la recta del tipo y = ax + b, con: a = 1 (pendiente positiva) y TK coeficiente de posición b = 273. Con esta información, el gráfico sería 273 TC

3. Gráficos Análisis directo de gráficos • Análisis visual de una función cuadrática o de segundo grado. Una función de segundo grado es aquella que presenta alguna de sus variables con exponente 2. Por ejemplo: y = x 2 El gráfico que genera una expresión cuadrática es una curva llamada parábola. y y x x

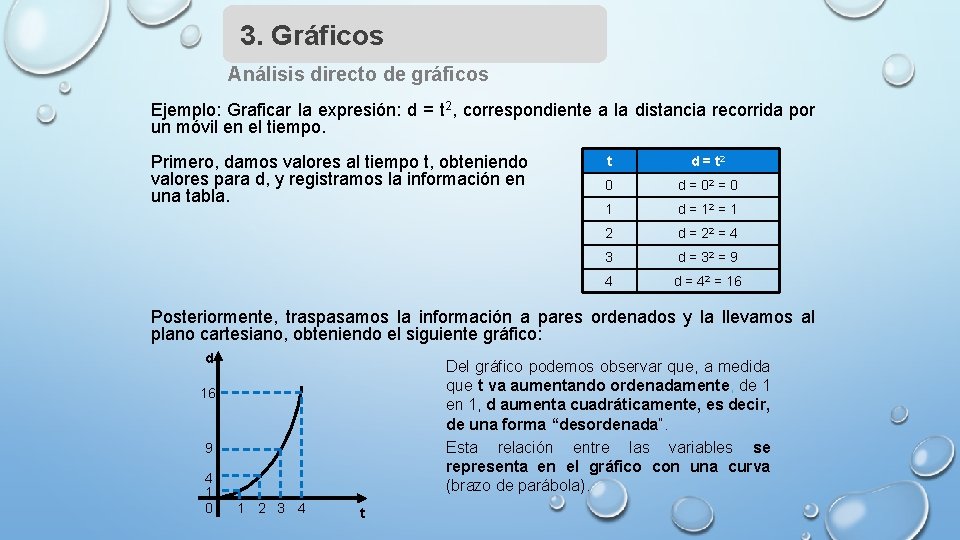
3. Gráficos Análisis directo de gráficos Ejemplo: Graficar la expresión: d = t 2, correspondiente a la distancia recorrida por un móvil en el tiempo. Primero, damos valores al tiempo t, obteniendo valores para d, y registramos la información en una tabla. t d = t 2 0 d = 02 = 0 1 d = 12 = 1 2 d = 22 = 4 3 d = 32 = 9 4 d = 42 = 16 Posteriormente, traspasamos la información a pares ordenados y la llevamos al plano cartesiano, obteniendo el siguiente gráfico: d Del gráfico podemos observar que, a medida que t va aumentando ordenadamente, de 1 en 1, d aumenta cuadráticamente, es decir, de una forma “desordenada”. Esta relación entre las variables se representa en el gráfico con una curva (brazo de parábola). 16 9 4 1 0 1 2 3 4 t

4. Magnitudes escalares Definición Son aquellas quedan claramente definidas por un número y una unidad de medida, es decir, los escalares solo poseen módulo. Algunas magnitudes escalares son: la longitud, el tiempo, la masa, la temperatura, etc. Ejemplos 3 [metros], 5 [horas], 1 [kilogramo], 10 [ºC]. En física se estudian magnitudes escalares como: trabajo, energía, temperatura y masa, entre otras.

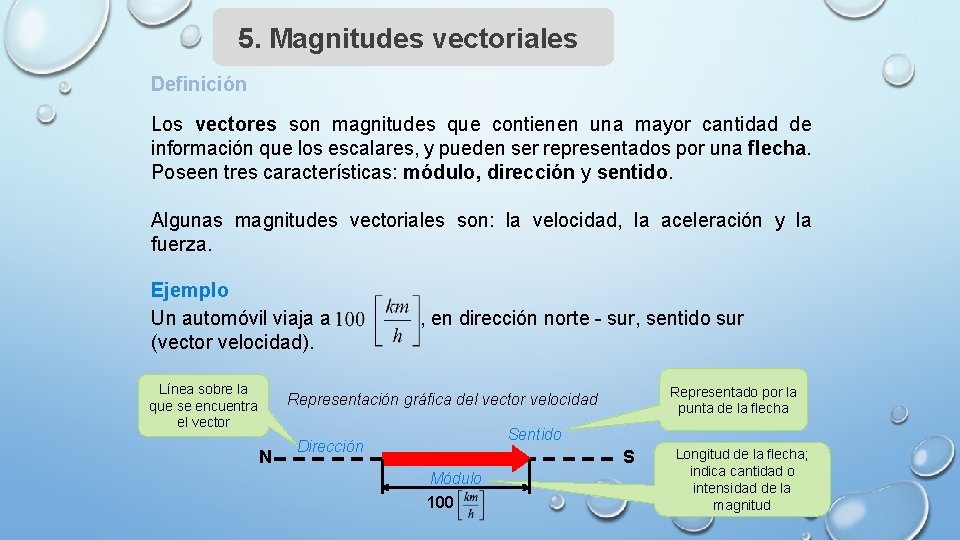
5. Magnitudes vectoriales Definición Los vectores son magnitudes que contienen una mayor cantidad de información que los escalares, y pueden ser representados por una flecha. Poseen tres características: módulo, dirección y sentido. Algunas magnitudes vectoriales son: la velocidad, la aceleración y la fuerza. Ejemplo Un automóvil viaja a (vector velocidad). Línea sobre la que se encuentra el vector , en dirección norte - sur, sentido sur Representado por la punta de la flecha Representación gráfica del vector velocidad N Sentido Dirección S Módulo 100 Longitud de la flecha; indica cantidad o intensidad de la magnitud

5. Magnitudes vectoriales Igualdad de vectores Dos vectores son iguales si sus características son iguales, es decir, si poseen igual módulo, dirección y sentido. Formas de expresar un vector Gráficamente Como par ordenado Mediante los vectores unitarios

5. Magnitudes vectoriales Componentes escalares de un vector Para poder expresar un vector como par ordenado, debemos conocer sus componentes escalares. La componente en x del vector es: La componente en y del vector es: Por lo tanto, el vector es

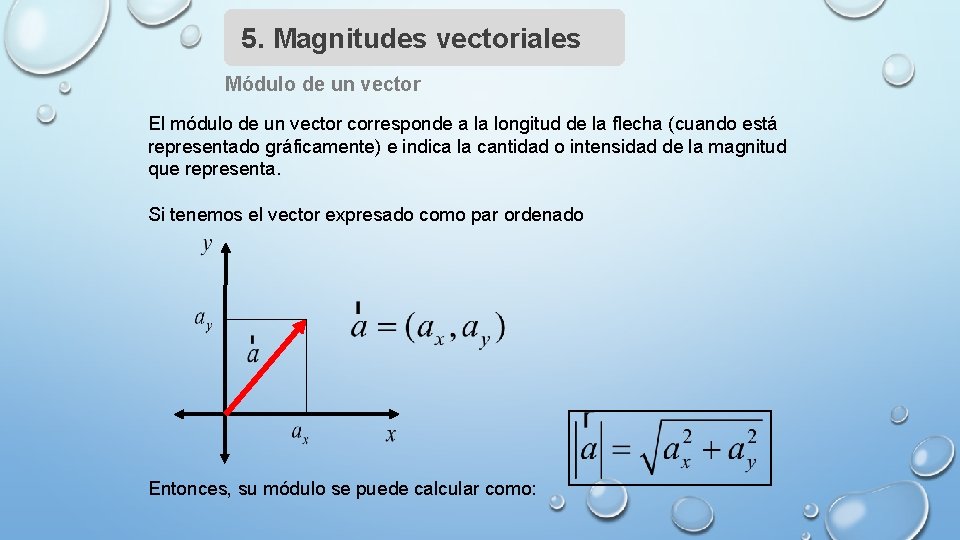
5. Magnitudes vectoriales Módulo de un vector El módulo de un vector corresponde a la longitud de la flecha (cuando está representado gráficamente) e indica la cantidad o intensidad de la magnitud que representa. Si tenemos el vector expresado como par ordenado Entonces, su módulo se puede calcular como:

6. Operaciones con vectores Ponderación de un vector La ponderación es una operación entre un vector y un escalar. Al ponderar un vector, este puede cambiar su módulo y su sentido (dependiendo del valor y signo del escalar), pero nunca cambia su dirección original.

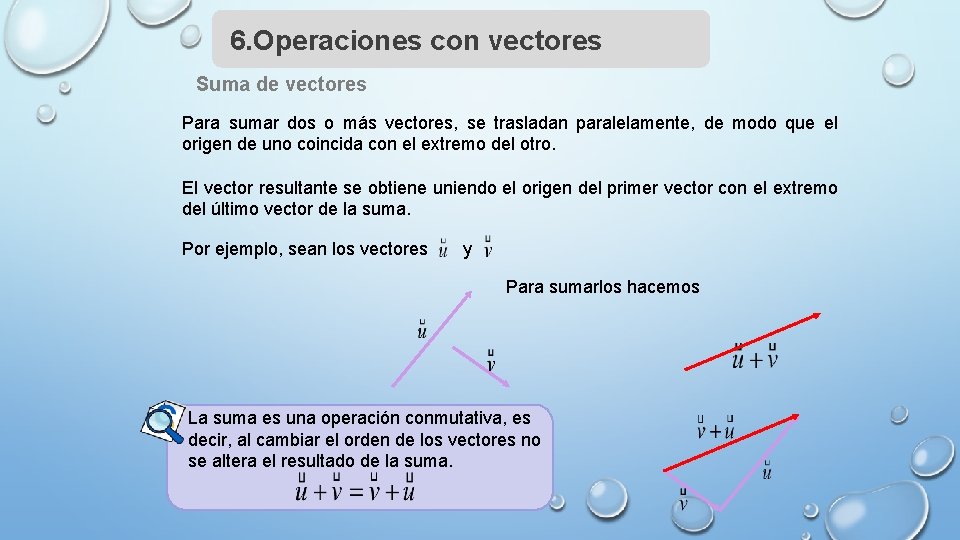
6. Operaciones con vectores Suma de vectores Para sumar dos o más vectores, se trasladan paralelamente, de modo que el origen de uno coincida con el extremo del otro. El vector resultante se obtiene uniendo el origen del primer vector con el extremo del último vector de la suma. Por ejemplo, sean los vectores y Para sumarlos hacemos La suma es una operación conmutativa, es decir, al cambiar el orden de los vectores no se altera el resultado de la suma.

6. Operaciones con vectores Resta de vectores Restar dos vectores es equivalente a sumar al primer vector el inverso aditivo del segundo. Por ejemplo, hagamos la resta : La resta no es una operación conmutativa, es decir, al cambiar el orden de los vectores se altera el resultado de la resta.

6. Operaciones con vectores Operatoria algebraica de vectores La suma de vectores es una operación muy fácil de realizar, cuando se trabaja con sus componentes algebraicas; basta sumar las componentes en x entre sí y hacer lo mismo con las componentes en y. Ejemplo Sean los vectores y El procedimiento para la resta de vectores es equivalente. . La suma será

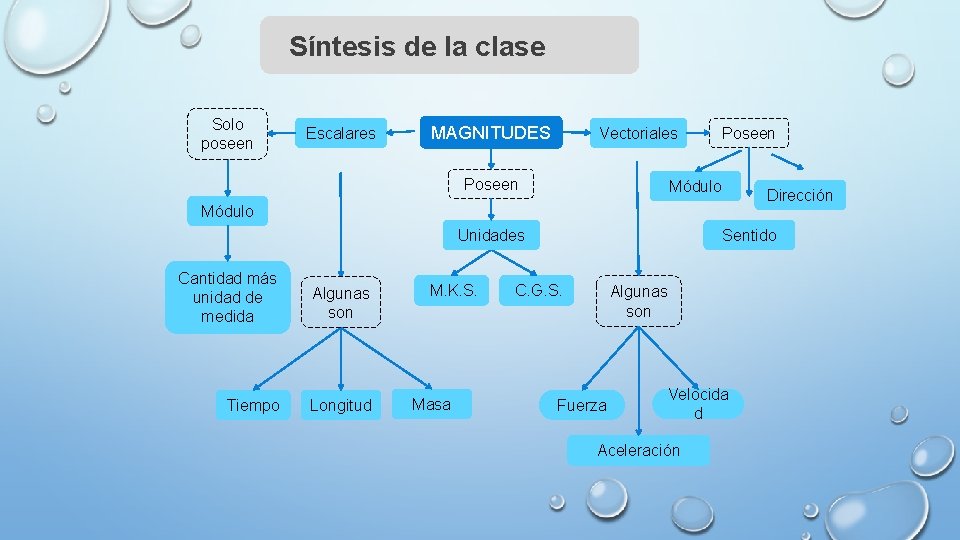
Síntesis de la clase Solo poseen Escalares MAGNITUDES Vectoriales Poseen Módulo Dirección Módulo Unidades Cantidad más unidad de medida Algunas son Tiempo Longitud M. K. S. Masa Sentido C. G. S. Algunas son Fuerza Velocida d Aceleración

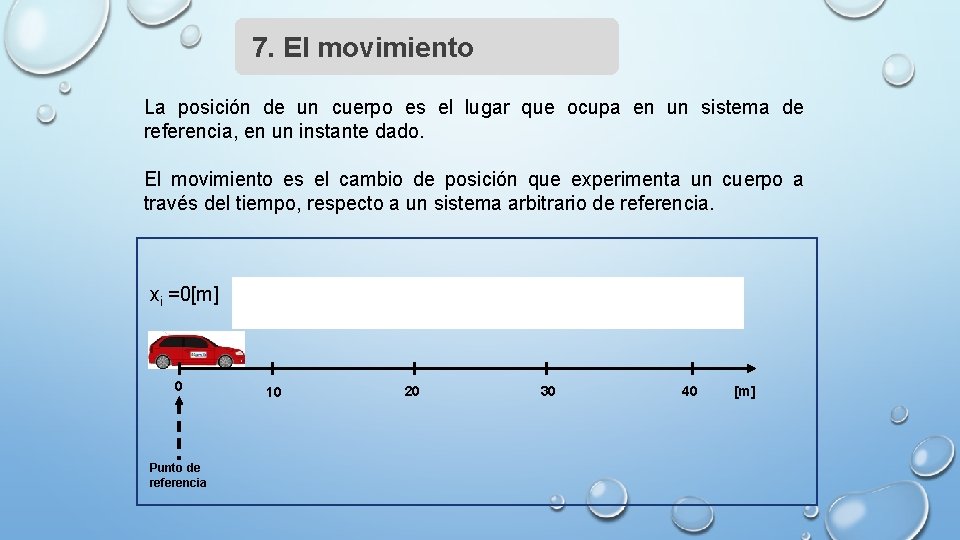
7. El movimiento La posición de un cuerpo es el lugar que ocupa en un sistema de referencia, en un instante dado. El movimiento es el cambio de posición que experimenta un cuerpo a través del tiempo, respecto a un sistema arbitrario de referencia. xi =0[m] 0 Punto de referencia xf =20[m] 10 20 xf =40[m] 30 40 [m]

7. El movimiento es relativo. Depende del sistema de referencia. Clasificación de los movimientos según el sistema de referencia • Movimiento relativo: El origen del sistema de referencia con el cual se observa el movimiento está, a su vez, en movimiento. • Movimiento absoluto: El origen del sistema de referencia con el cual se observa el movimiento está en reposo. Utilizaremos solo sistemas de referencias absolutos para nuestro estudio.

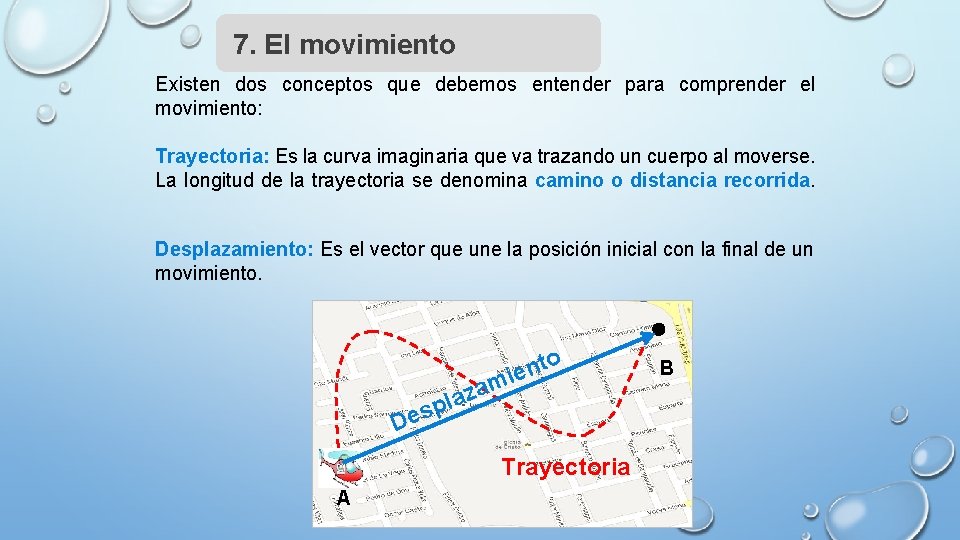
7. El movimiento Existen dos conceptos que debemos entender para comprender el movimiento: Trayectoria: Es la curva imaginaria que va trazando un cuerpo al moverse. La longitud de la trayectoria se denomina camino o distancia recorrida. Desplazamiento: Es el vector que une la posición inicial con la final de un movimiento. a az l p s o t n mie De Trayectoria A B

7. El movimiento Clasificación de los movimientos según su trayectoria Movimiento rectilíneo: La trayectoria que describe el móvil es una línea recta. Ejemplo: La caída de una manzana desde un árbol. Movimiento curvilíneo: La trayectoria que describe el móvil es una curva. Ejemplo: El movimiento de la jabalina al ser lanzada.

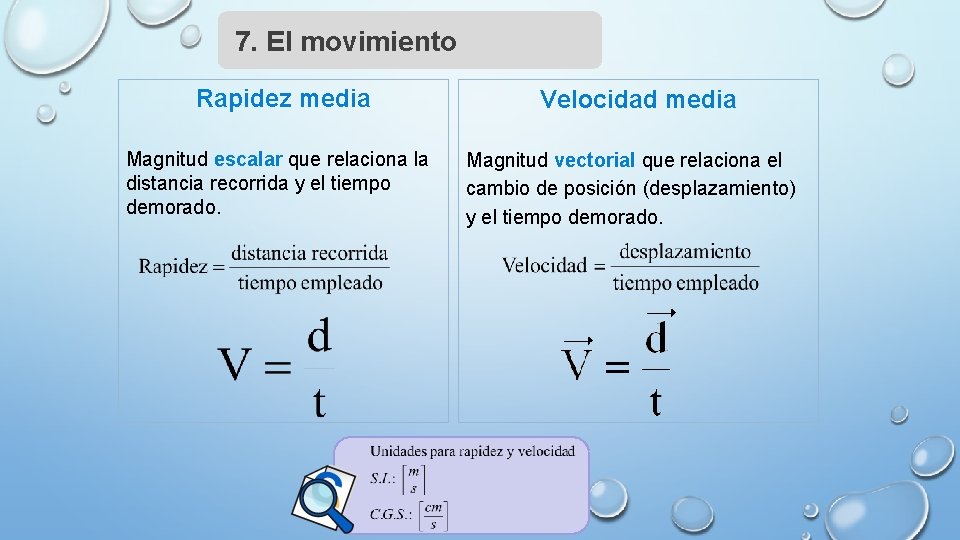
7. El movimiento Rapidez media Magnitud escalar que relaciona la distancia recorrida y el tiempo demorado. Velocidad media Magnitud vectorial que relaciona el cambio de posición (desplazamiento) y el tiempo demorado.

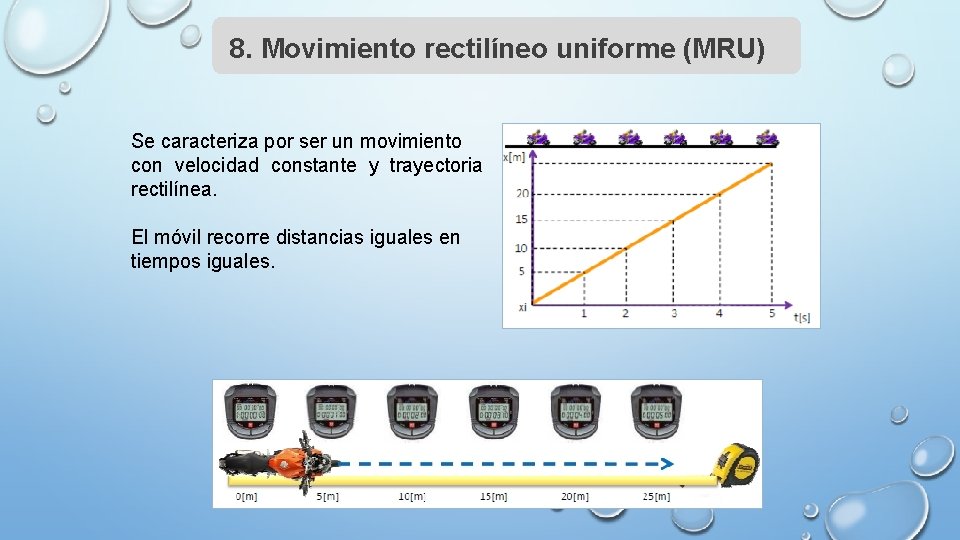
8. Movimiento rectilíneo uniforme (MRU) Se caracteriza por ser un movimiento con velocidad constante y trayectoria rectilínea. El móvil recorre distancias iguales en tiempos iguales.

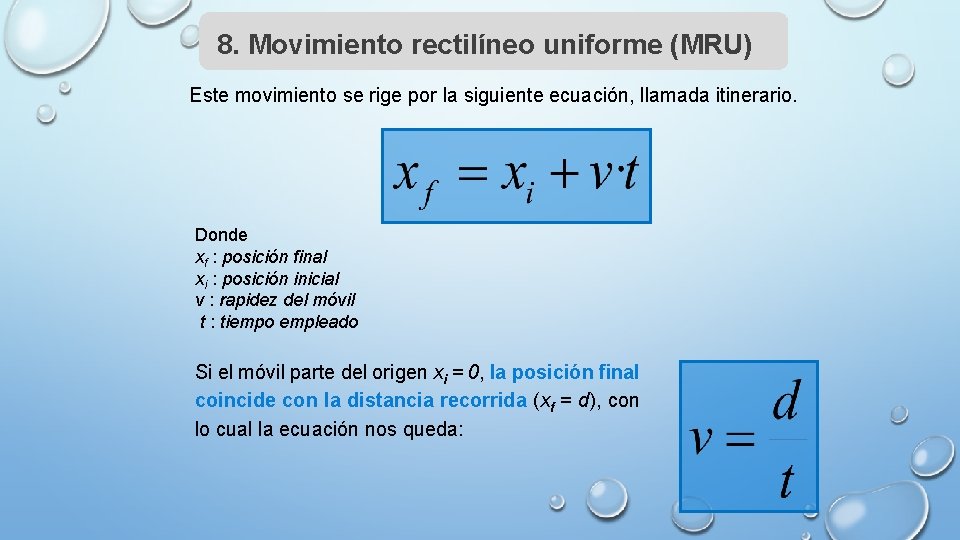
8. Movimiento rectilíneo uniforme (MRU) Este movimiento se rige por la siguiente ecuación, llamada itinerario. Donde xf : posición final xi : posición inicial v : rapidez del móvil t : tiempo empleado Si el móvil parte del origen xi = 0, la posición final coincide con la distancia recorrida (xf = d), con lo cual la ecuación nos queda:

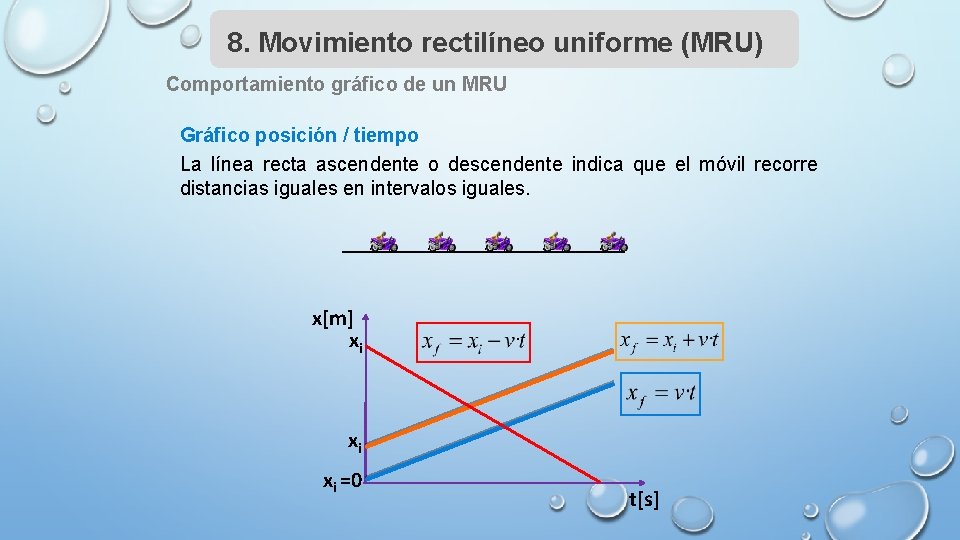
8. Movimiento rectilíneo uniforme (MRU) Comportamiento gráfico de un MRU Gráfico posición / tiempo La línea recta ascendente o descendente indica que el móvil recorre distancias iguales en intervalos iguales. x[m] xi xi xi =0 t[s]

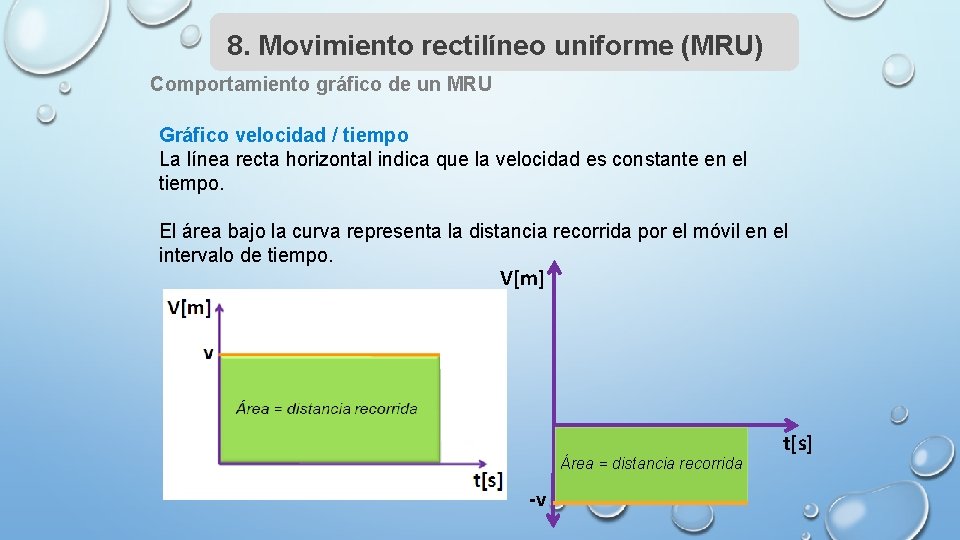
8. Movimiento rectilíneo uniforme (MRU) Comportamiento gráfico de un MRU Gráfico velocidad / tiempo La línea recta horizontal indica que la velocidad es constante en el tiempo. El área bajo la curva representa la distancia recorrida por el móvil en el intervalo de tiempo. V[m] Área = distancia recorrida -v t[s]

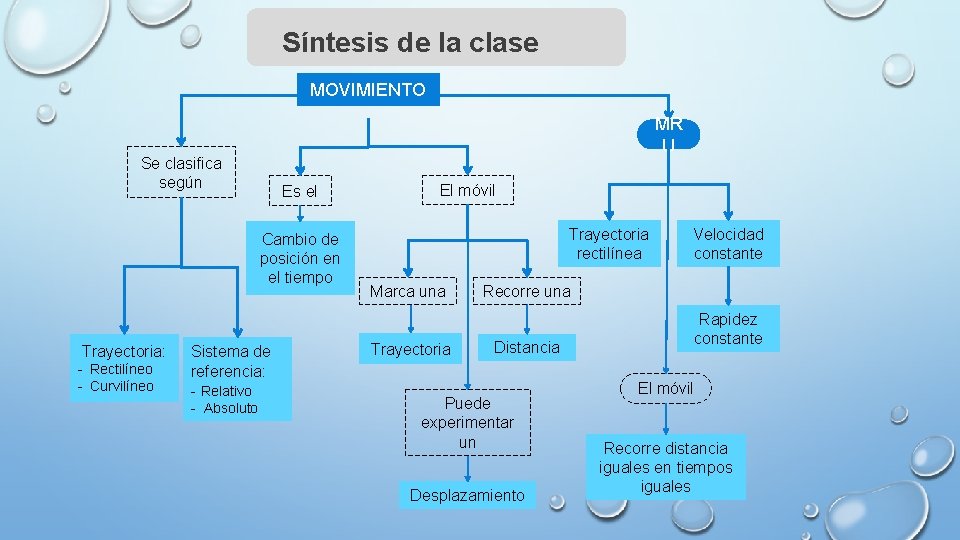
Síntesis de la clase MOVIMIENTO MR U Se clasifica según Es el Cambio de posición en el tiempo Trayectoria: - Rectilíneo - Curvilíneo Sistema de referencia: - Relativo - Absoluto El móvil Trayectoria rectilínea Marca una Trayectoria Velocidad constante Recorre una Distancia Puede experimentar un Desplazamiento Rapidez constante El móvil Recorre distancia iguales en tiempos iguales