Unidad I Suma y resta de fracciones Objetivo

Unidad I: Suma y resta de fracciones. Objetivo: Resolver sumas y restas de fracciones. -Sexto básico 2020 Colegio Antupirén. -Semana del 30 de marzo al 3 de abril. -Profesores: Pablo Arriagada/ Jaime Soto A.

• Recuerda que, el numerador de una fracción corresponde al número de arriba y el denominador al número de abajo.

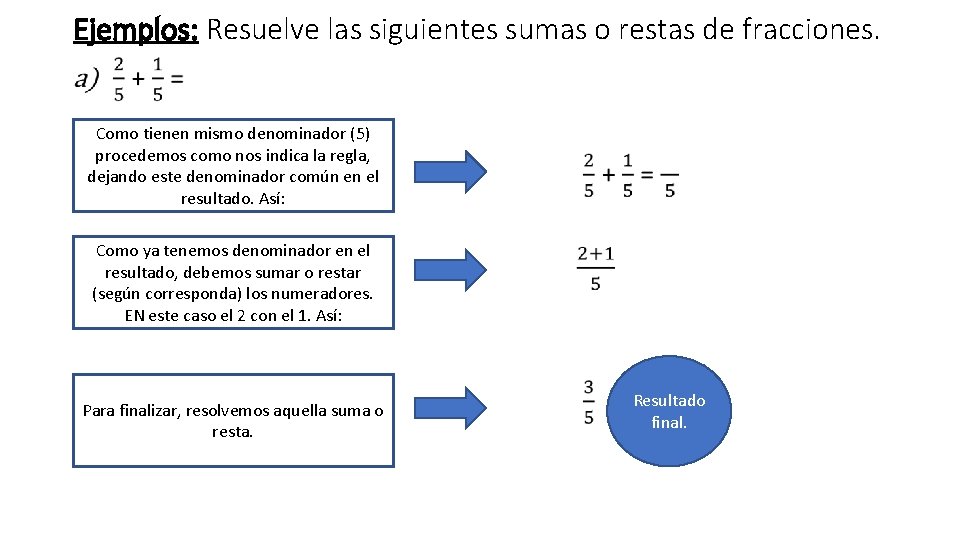
Ejemplos: Resuelve las siguientes sumas o restas de fracciones. • Como tienen mismo denominador (5) procedemos como nos indica la regla, dejando este denominador común en el resultado. Así: Como ya tenemos denominador en el resultado, debemos sumar o restar (según corresponda) los numeradores. EN este caso el 2 con el 1. Así: Para finalizar, resolvemos aquella suma o resta. Resultado final.

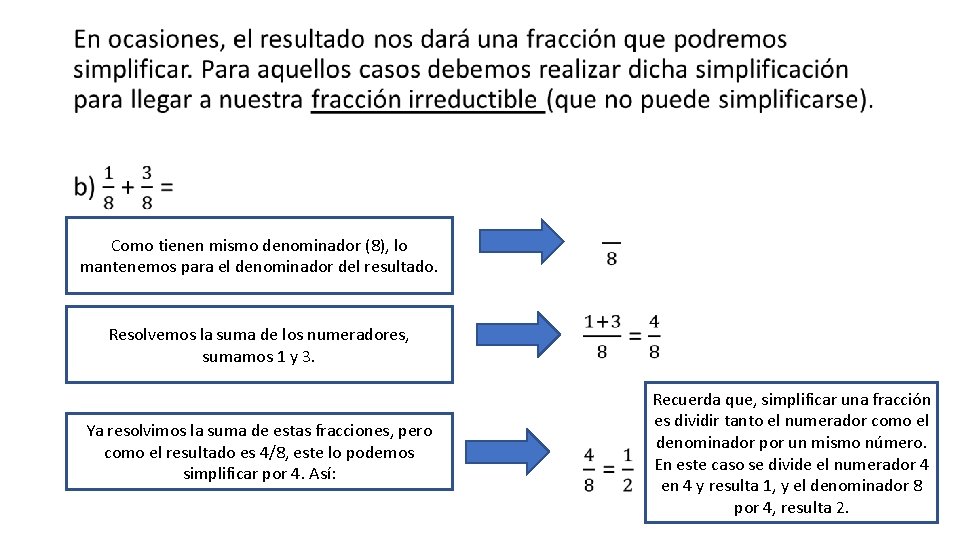
• Como tienen mismo denominador (8), lo mantenemos para el denominador del resultado. Resolvemos la suma de los numeradores, sumamos 1 y 3. Ya resolvimos la suma de estas fracciones, pero como el resultado es 4/8, este lo podemos simplificar por 4. Así: Recuerda que, simplificar una fracción es dividir tanto el numerador como el denominador por un mismo número. En este caso se divide el numerador 4 en 4 y resulta 1, y el denominador 8 por 4, resulta 2.

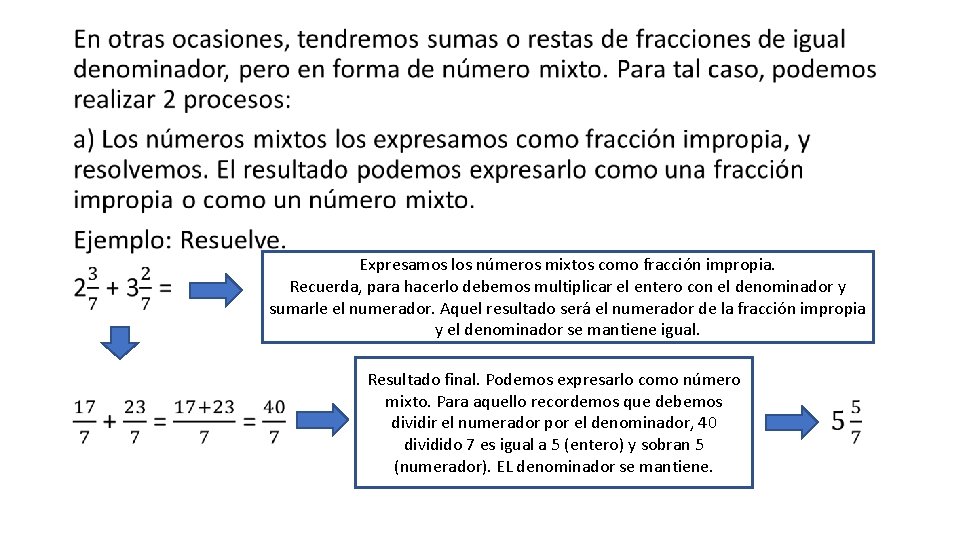
• Expresamos los números mixtos como fracción impropia. Recuerda, para hacerlo debemos multiplicar el entero con el denominador y sumarle el numerador. Aquel resultado será el numerador de la fracción impropia y el denominador se mantiene igual. Resultado final. Podemos expresarlo como número mixto. Para aquello recordemos que debemos dividir el numerador por el denominador, 40 dividido 7 es igual a 5 (entero) y sobran 5 (numerador). EL denominador se mantiene.

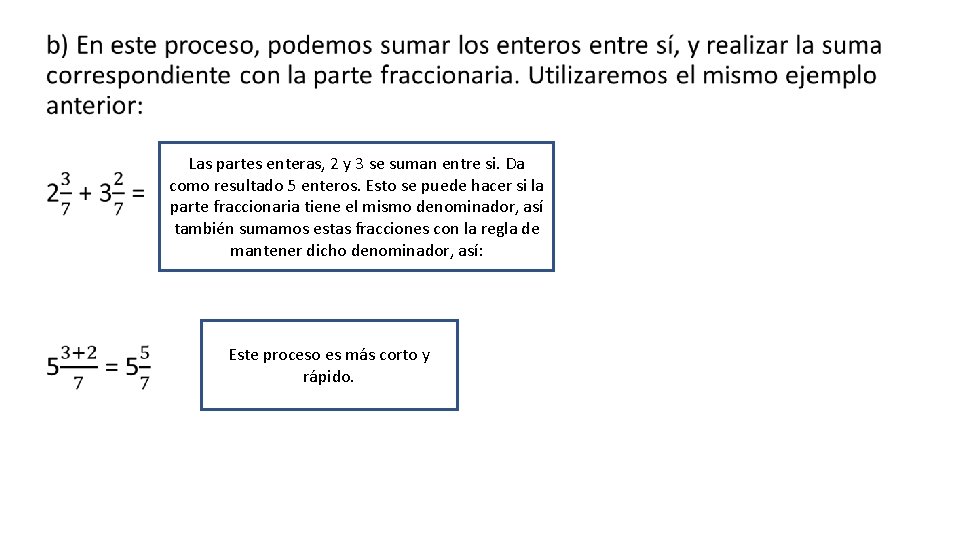
• Las partes enteras, 2 y 3 se suman entre si. Da como resultado 5 enteros. Esto se puede hacer si la parte fraccionaria tiene el mismo denominador, así también sumamos estas fracciones con la regla de mantener dicho denominador, así: Este proceso es más corto y rápido.

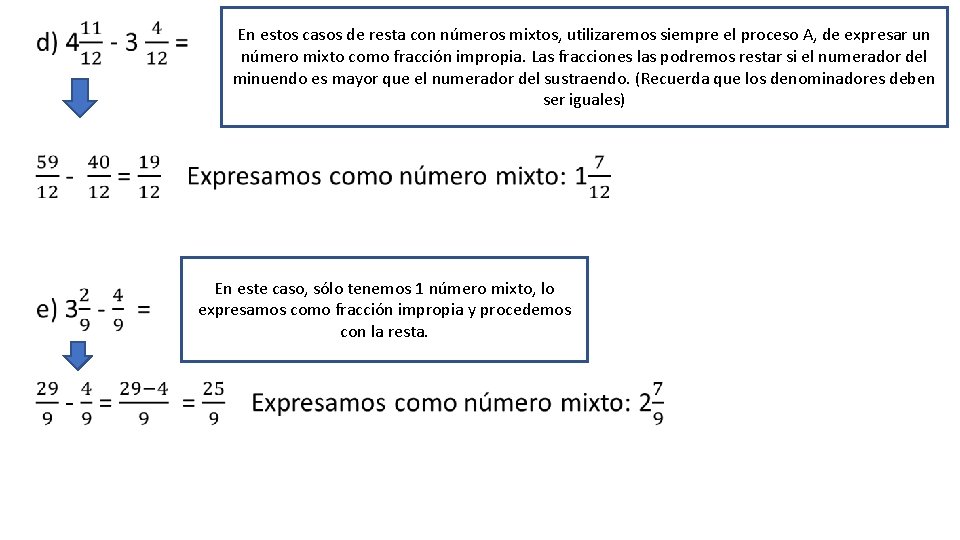
• En estos casos de resta con números mixtos, utilizaremos siempre el proceso A, de expresar un número mixto como fracción impropia. Las fracciones las podremos restar si el numerador del minuendo es mayor que el numerador del sustraendo. (Recuerda que los denominadores deben ser iguales) En este caso, sólo tenemos 1 número mixto, lo expresamos como fracción impropia y procedemos con la resta.

Caso 2: Suma y resta de fracciones con DISTINTO denominador. En este caso se tienen diversas situaciones, las cuales cada una tiene un método apropiado para resolver. Lo importante a entender es que, para poder sumar o restar fracciones, debemos siempre IGUALAR DENOMINADORES, y para aquello en diversas situaciones, nos ayudará el concepto de mínimo común múltiplo y amplificación, aquello lo veremos la siguiente clase. Recuerda: Amplificar una fracción es multiplicar tanto el numerador y el denominador por una misma cantidad.

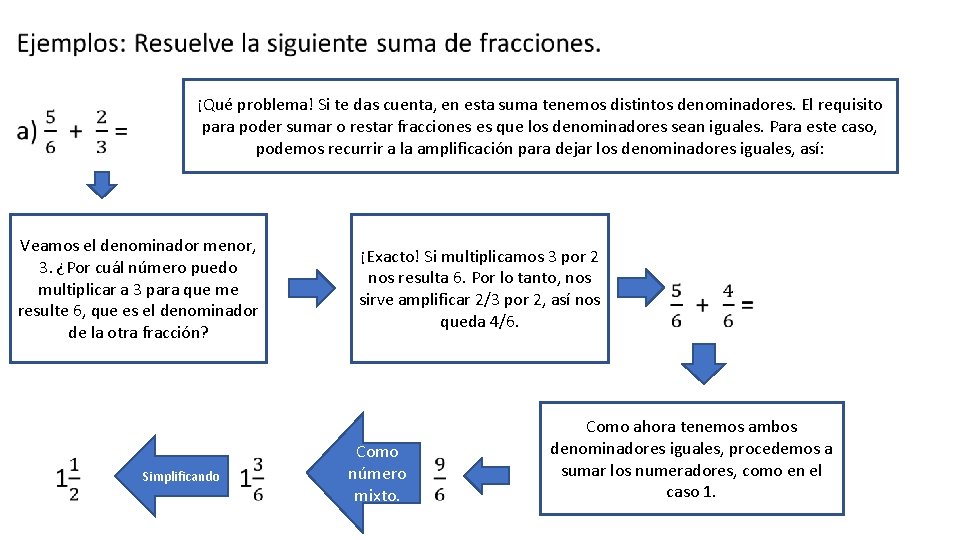
• ¡Qué problema! Si te das cuenta, en esta suma tenemos distintos denominadores. El requisito para poder sumar o restar fracciones es que los denominadores sean iguales. Para este caso, podemos recurrir a la amplificación para dejar los denominadores iguales, así: Veamos el denominador menor, 3. ¿Por cuál número puedo multiplicar a 3 para que me resulte 6, que es el denominador de la otra fracción? Simplificando ¡Exacto! Si multiplicamos 3 por 2 nos resulta 6. Por lo tanto, nos sirve amplificar 2/3 por 2, así nos queda 4/6. Como número mixto. Como ahora tenemos ambos denominadores iguales, procedemos a sumar los numeradores, como en el caso 1.

• Nuevamente, tenemos suma de distinto denominador. Pero, podemos amplificar la primera fracción 3/5 por 3, así nuestro denominador nos dará 15, que será igual al otro denominador.