Unidad 4 Abstracciones de Datos y Algoritmia Concepto

Unidad 4: Abstracciones de Datos y Algoritmia Concepto de Algoritmo. Recursos que requiere un algoritmo. Operación elemental. Principio de Invarianza. Análisis del Caso Mejor, Peor y Medio. Eficiencia. Importancia de la eficiencia. Notación asintótica. Ecuaciones Complejidad Computacional. Ecuaciones de recurrencia. Programación I (Plan 1999) Algoritmos y Estructuras de Datos II (Plan 2009) Mgter. Oscar Adolfo Vallejos Fa. CENA - UNNE

Objetivos El concepto de correctitud de un algoritmo debe no sólo incluir el hecho de que el algoritmo realice lo especificado, sino también que lo realice con los recursos disponibles. Los recursos más limitados en la producción de software son: el tiempo de ejecución (medido en cantidad instrucciones elementales) la memoria para el almacenamiento de los datos (medida en general en cantidad de variables elementales). Se denomina a estas funciones medidas de complejidad

Complejidad Computacional Para resolver estos problemas se necesita una mejora en los algoritmos; pero no una pequeña mejora sino una mejora en órdenes de magnitud. Ej. : una búsqueda secuencial en un arreglo ordenado es de (n) en el peor caso; una búsqueda binaria es de (log n). Para instancias pequeñas la diferencia puede no ser notable, pero para n = 109 la diferencia está entre esperar un año o un minuto por el resultado. Dado un algoritmo que resuelve un problema, es razonable (y aconsejable) preguntarse si no existirá un algoritmo más eficiente para el mismo problema el objetivo fundamental de la Complejidad Computacional es clasificar los problemas de acuerdo a su tratabilidad, tomando el o los algoritmos más eficientes para resolverlos

Clasificación de problemas De acuerdo al estado de conocimiento de sus algoritmos – cerrado – abierto De acuerdo a los recursos indispensables para su solución – tratables – intratables

Para cerrar un problema se puede hacer : Encontrar un algoritmo asintóticamente mejor que los que se conocen. Demostrar una cota asintóticamente superior de las que se conocen.

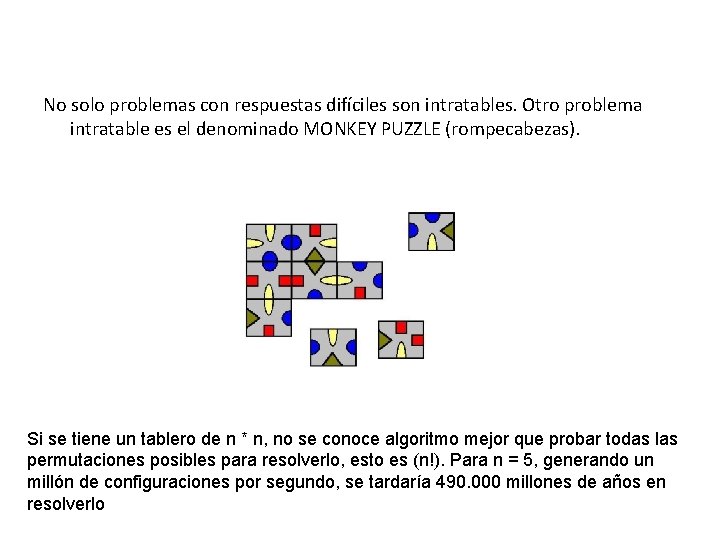
No solo problemas con respuestas difíciles son intratables. Otro problema intratable es el denominado MONKEY PUZZLE (rompecabezas). Si se tiene un tablero de n * n, no se conoce algoritmo mejor que probar todas las permutaciones posibles para resolverlo, esto es (n!). Para n = 5, generando un millón de configuraciones por segundo, se tardaría 490. 000 millones de años en resolverlo

Los algoritmos de O(nk ) son considerados de tiempo razonable a pesar del k y de las posibles constantes ocultas para el espacio de memoria se tiene que tener más cuidado, porque ya un espacio polinomial muchas veces es intratable las funciones exponenciales y factoriales siempre son intratables además, dentro de esta tratabilidad y de esta intratabilidad es posible distinguir varios grados otro tema de investigación actual es la extensión del concepto de tratabilidad a algoritmos probabilísticos y paralelos. En estos casos se han propuesto otras formalizaciones

Conceptos básicos Con el objetivo de simplificar la clasificación, sólo se considerarán problemas de decisión (Tienen como respuesta sí o no). Los problemas que no son de decisión se analizan en forma separada, pero la mayoría se puede reducir a algún problema de decisión. A pesar de esta clasificación el espectro de problemas sigue siendo muy amplio.

LA COMPLEJIDAD DE LOS ALGORITMOS • En un sentido amplio, dado un problema y un dispositivo donde resolverlo, es necesario proporcionar un método preciso que lo resuelva, adecuado al dispositivo. (algoritmo). • Es necesario centrarse en dos aspectos muy importantes de los algoritmos, como son su diseño y el estudio de su eficiencia. • El primero se refiere a la búsqueda de métodos o procedimientos, secuencias finitas de instrucciones adecuadas al dispositivo que disponemos, que permitan resolver el problema. • El segundo nos permite medir de alguna forma el coste (en tiempo y recursos) que consume un algoritmo para encontrar la solución y nos ofrece la posibilidad de comparar distintos algoritmos que resuelven un mismo problema.

EFICIENCIA Y COMPLEJIDAD § Una vez que dispongamos de un algoritmo que funciona correctamente, es necesario definir criterios para medir su rendimiento o comportamiento. § Estos criterios se centran principalmente en su simplicidad y en el uso eficiente de los recursos. § Un algoritmo sencillo no es muy eficiente. Sin embargo, la sencillez es una característica muy interesante a la hora de diseñar un algoritmo, pues facilita su verificación, el estudio de su eficiencia y su mantenimiento. De ahí que muchas veces prime la simplicidad y legibilidad del código frente a alternativas más crípticas y eficientes del algoritmo. Ej. : Método de ordenación Burbujas Vs. Shell. Sort § El uso eficiente de los recursos suele medirse en función de dos parámetros: el espacio (memoria) , y el tiempo, lo que tarda en ejecutarse.

La eficiencia es la razón entre el beneficio obtenido y los medios empleados

Importancia de la Eficiencia Intentar diseñar algoritmos eficientes cuando se dispone de maquinas cada vez mas potentes y capaces de realizar tareas cada vez mas complejas, puede ser poco lógico.

Tiempo de ejecución El tiempo de ejecución de un algoritmo va a depender de diversos factores como son: los datos de entrada que le suministremos, la calidad del código generado por el compilador para crear el programa objeto, la naturaleza y rapidez de las instrucciones máquina del procesador concreto que ejecute el programa, y la complejidad intrínseca del algoritmo. Hay dos estudios posibles sobre el tiempo: 1. Uno que proporciona una medida teórica (a priori), que consiste en obtener una función que acote (por arriba o por abajo) el tiempo de ejecución del algoritmo para unos valores de entrada dados. 2. Y otro que ofrece una medida real – empírico (a posteriori), consistente en medir el tiempo de ejecución del algoritmo para unos valores de entrada dados y en un ordenador concreto.

Tiempo de ejecución Ambas medidas son importantes puesto que, si bien la primera nos ofrece estimaciones del comportamiento de los algoritmos de forma independiente del ordenador en donde serán implementados y sin necesidad de ejecutarlos, la segunda representa las medidas reales del comportamiento del algoritmo. Estas medidas son funciones temporales de los datos de entrada. Entendemos por tamaño de la entrada el número de componentes sobre los que se va a ejecutar el algoritmo. Ej. : la dimensión del vector a ordenar o el tamaño de las matrices a multiplicar. La unidad de tiempo a la que debe hacer referencia estas medidas de eficiencia no puede ser expresada en segundos o en otra unidad de tiempo concreta, pues no existe un ordenador estándar al que puedan hacer referencia todas las medidas. Denotaremos por T(n) el tiempo de ejecución de un algoritmo para una entrada de tamaño n.

Principio de Invarianza Teóricamente T(n) debe indicar el número de instrucciones ejecutadas por un ordenador idealizado. Debemos buscar por tanto medidas simples y abstractas, independientes del ordenador a utilizar. Para ello es necesario acotar de alguna forma la diferencia que se puede producir entre distintas implementaciones de un mismo algoritmo, ya sea del mismo código ejecutado por dos máquinas de distinta velocidad, como de dos códigos que implementen el mismo método. Esta diferencia es la que acota el siguiente principio: Dado un algoritmo y dos implementaciones suyas I 1 e I 2, que tardan T 1(n) y T 2(n) segundos respectivamente, el Principio de Invarianza afirma que existe una constante real c > 0 y un número natural n 0 tales que para todo n ≥ n 0 se verifica que T 1(n) ≤ c. T 2(n). Con esto podemos definir sin problemas que un algoritmo tarda un tiempo del orden de T(n) si existen una constante real c > 0 y una implementación I del algoritmo que tarda menos que c. T(n), para todo n tamaño de la entrada.

Principio de Invarianza También es importante hacer notar que el comportamiento de un algoritmo puede cambiar notablemente para diferentes entradas (por ejemplo, lo ordenados que se encuentren ya los datos a ordenar). De hecho, para muchos programas el tiempo de ejecución es en realidad una función de la entrada específica, y no sólo de tamaño de ésta. Así suelen estudiarse tres casos para un mismo algoritmo: caso peor, caso mejor y caso medio. Caso mejor corresponde a la traza (secuencia de sentencias) del algoritmo que realiza menos instrucciones. Caso peor corresponde a la traza del algoritmo que realiza más instrucciones. Caso medio, corresponde a la traza del algoritmo que realiza un número de instrucciones igual a la esperanza matemática de la variable aleatoria definida por todas las posibles trazas del algoritmo para un tamaño de la entrada dado, con las probabilidades de que éstas ocurran para esa entrada.

A la hora de medir el tiempo, siempre lo haremos en función del número de operaciones elementales que realiza dicho algoritmo, entendiendo por operaciones elementales (OE) aquellas que el ordenador realiza en tiempo acotado por una constante. Así, consideraremos OE las operaciones aritméticas básicas, asignaciones a variables de tipo predefinido por el compilador, los saltos (llamadas a funciones y procedimientos, retorno desde ellos, etc. ), las comparaciones lógicas y el acceso a estructuras indexadas básicas, como son los vectores y matrices. Cada una de ellas contabilizará como 1 OE. Resumiendo, el tiempo de ejecución de un algoritmo va a ser una función que mide el número de operaciones elementales que realiza el algoritmo para un tamaño de entrada dado.

ECUACIONES EN RECURRENCIA En las secciones anteriores hemos descrito cómo determinar el tiempo de ejecución de un algoritmo a partir del cómputo de sus operaciones elementales (OE). En general, este cómputo se reduce a un mero ejercicio de cálculo. Sin embargo, para los algoritmos recursivos nos vamos a encontrar con una dificultad añadida, pues la función que establece su tiempo de ejecución viene dada por una ecuación en recurrencia, es decir, T(n) = E(n), en donde en la expresión E aparece la propia función T. Resolver tal tipo de ecuaciones consiste en encontrar una expresión no recursiva de T, y por lo general no es una labor fácil. Homogéneas a 0 T(n) + a 1 T(n − 1) + a 2 T(n − 2) +. . . + ak. T(n − k) = 0 No homogéneas a 0 T(n) + a 1 T(n − 1) +. . . + ak T(n − k) = b np(n)

COTAS DE COMPLEJIDAD. MEDIDAS ASINTÓTICAS Cota Superior. Notación O: Dada una función f, queremos estudiar aquellas funciones g que a lo sumo crecen tan deprisa como f. Al conjunto de tales funciones se le llama cota superior de f y lo denominamos O(f). Conociendo la cota superior de un algoritmo podemos asegurar que, en ningún caso, el tiempo empleado será de un orden superior al de la cota. Cota Inferior. Notación Ω: Dada una función f, queremos estudiar aquellas funciones g que a lo sumo crecen tan lentamente como f. Al conjunto de tales funciones se le llama cota inferior de f y lo denominamos Ω(f). Conociendo la cota inferior de un algoritmo podemos asegurar que, en ningún caso, el tiempo empleado será de un orden inferior al de la cota. Orden Exacto. Notación Θ: Como última cota asintótica, definiremos los conjuntos de funciones que crecen asintóticamente de la misma forma.

complejidad computacional Es la rama de la teoría de la computación que estudia, de manera teórica, la complejidad inherente a la resolución de un problema computable. Los recursos comúnmente estudiados son el tiempo (mediante una aproximación al número y tipo de pasos de ejecución de un algoritmo para resolver un problema) y el espacio (mediante una aproximación a la cantidad de memoria utilizada para resolver un problema). Se pueden estudiar igualmente otros parámetros, tales como el número de procesadores necesarios para resolver el problema en paralelo. La teoría de la complejidad difiere de la teoría de la computabilidad en que ésta se ocupa de la factibilidad de expresar problemas como algoritmos efectivos sin tomar en cuenta los recursos necesarios para ello.

Complejidad Computacional Hoy en día las computadoras resuelven problemas mediante algoritmos que tienen como máximo una complejidad o coste computacional polinómico, es decir, la relación entre el tamaño del problema y su tiempo de ejecución es polinómica. Éstos son problemas agrupados en la clase P. Los problemas que no pueden ser resueltos por nuestras computadoras (las cuales son Máquinas Determinísticas), que en general poseen costes factorial o combinatorio pero que podrían ser procesados por una máquina no-determinista, están agrupados en la clase NP. Estos problemas no tienen una solución práctica, es decir, una máquina determinística (como una computadora actual) no puede resolverlos en un tiempo razonable.

Problemas de decisión La mayor parte de los problemas en teoría de la complejidad tienen que ver con los problemas de decisión, que corresponden a poder dar una respuesta positiva o negativa a un problema dado. Por ejemplo, el problema ES-PRIMO se puede describir como: Dado un entero, responder si ese número es primo o no. Un problema de decisión es equivalente a un lenguaje formal, que es un conjunto de palabras de longitud finita en un lenguaje dado. Para un problema de decisión dado, el lenguaje equivalente es el conjunto de entradas para el cual la respuesta es positiva.

Problemas de decisión Los problemas de decisión son importantes porque casi todo problema puede ser transformado en un problema de decisión. Por ejemplo el problema CONTIENE-FACTORES descrito como: Dados enteros n y k, decidir si n tiene algún factor menor que k. Si se puede resolver CONTIENE-FACTORES con una cierta cantidad de recursos, su solución se puede utilizar para resolver FACTORIZAR con los mismos recursos, realizando una búsqueda binaria sobre k hasta encontrar el más pequeño factor de n, luego se divide ese factor y se repite el proceso hasta encontrar todos los factores.

Problemas de decisión En teoría de la complejidad, generalmente se distingue entre soluciones positivas o negativas. Por ejemplo, el conjunto P se define como el conjunto de los problemas en donde las respuestas positivas pueden ser verificadas muy rápidamente (es decir, en tiempo polinómico). El conjunto Co-P es el conjunto de problemas donde las respuestas negativas pueden ser verificadas rápidamente. El prefijo "Co" abrevia "complemento". El complemento de un problema es aquel en donde las respuestas positivas y negativas están intercambiadas, como entre ES-COMPUESTO y ES-PRIMO.

Clases de complejidad La clase de complejidad P es el conjunto de los problemas de decisión que pueden ser resueltos en una máquina determinista en tiempo polinómico, lo que corresponde intuitivamente a problemas que pueden ser resueltos aún en el peor de sus casos. La clase de complejidad NP es el conjunto de los problemas de decisión que pueden ser resueltos por una máquina no determinista en tiempo polinómico. Esta clase contiene muchos problemas que se desean resolver en la práctica, incluyendo el problema de satisfacibilidad booleana y el problema del viajante, un camino Hamiltoniano para recorrer todos los vértices una sola vez. Todos los problemas de esta clase tienen la propiedad de que su solución puede ser verificada efectivamente.

La pregunta P=NP El saber si las clases P y NP son iguales es el más importante problema abierto en Computación teórica. Un conjunto X de problemas es duro con respecto a un conjunto de problemas Y ( 'Y' pertenecientes a NP) si X>Y o X=Y, es decir Y se puede escribir como un conjunto de soluciones de los problemas X. En palabras simples, Y es "más sencillo" que X. El término sencillo se define precisamente en cada caso. El conjunto duro más importante es NP-duro. El conjunto X es completo para Y si es duro para Y y es también un subconjunto de Y (caso X=Y). El conjunto completo más importante es NP-completo. En otras palabras, los problemas del conjunto NP-completo tienen la característica de que, si se llega a encontrar una solución en tiempo P para algún miembro del conjunto (cualquiera de los problemas de NP-completo), entonces de hecho existe una solución en tiempo P para todos los problemas de NP-completo.

Problemas incompletos en NP Otra pregunta abierta relacionada con el problema P = NP es si existen problemas que estén en NP, pero no en P, que no sean NP-Completos. En otras palabras, problemas que tengan que ser resueltos en tiempo polinomial no-determinista, pero que no puedan ser reducidos a tiempo polinomial desde otros problemas con tiempo polinomial nodeterminista. Uno de tales problemas que se sabe que es NP pero no se sabe si es NPcompleto, es el problema de isomorfismo de grafos, un algoritmo que decide si dos grafos son isomorfos (por ejemplo: comparten las mismas propiedades). Se ha demostrado que si P ≠ NP entonces dicho algoritmo existe.

Intratabilidad Los problemas que pueden ser resueltos en teoría, pero no en práctica, se llaman intratables. Qué se puede y qué no en la práctica es un tema debatible, pero en general sólo los problemas que tienen soluciones de tiempos polinomiales son solubles para más que unos cuantos valores. Entre los problemas intratables se incluyen los de EXPTIME-completo. Si NP no es igual a P, entonces todos los problemas de NP-completo son también intratables. Para ver por qué las soluciones de tiempo exponencial no son útiles en la práctica, se puede considerar un problema que requiera 2 n operaciones para su resolución (n es el tamaño de la fuente de información). Para una fuente de información relativamente pequeña, n=100, y asumiendo que una computadora puede llevar a cabo 1010 (10 giga) operaciones por segundo, una solución llevaría cerca de 4*1012 años para completarse.