UNIDAD 2 CAPTULO VII ECUACIONES LINEALES U2 CAP













- Slides: 13

UNIDAD 2 CAPÍTULO VII ECUACIONES LINEALES

U-2. CAP. VII. ECUACIONES LINEALES Una vez establecida y aceptada la relevancia que tienen los factores integrantes en la solución de ecuaciones diferenciales es posible abordar las ecuaciones lineales de primer orden, cuya forma estándar es la siguiente: en donde p y q son funciones estrictas de la variable x y se suponen continuas en un intervalo dado. Se propone resolver esta ecuación mediante la búsqueda de un factor integrante m (x) que, al multiplicar a la ecuación lineal, transforme su miembro izquierdo en la derivada de una sola expresión.

U-2. CAP. VII. ECUACIONES LINEALES Es decir, que en el producto el miembro izquierdo sea análogo a la derivada así de donde, al simplificar se obtiene una ecuación de variables separables

U-2. CAP. VII. ECUACIONES LINEALES La aplicación de operador integral a esta última ecuación permite obtener el factor integrante en la forma: siempre que la integral exista. Aquí se omite la constante de integración C ya que su inclusión produce la misma solución multiplicada por una constante. La hipótesis asegura también que la ecuación diferencial es equivalente a

U-2. CAP. VII. ECUACIONES LINEALES siendo esta última una ecuación que se resuelve mediante una integración directa para producir la solución general de la ecuación lineal: donde el factor integrante m (x) es el anteriormente obtenido y la constante de integración C se determina a través de la condición inicial.

U-2. CAP. VII. ECUACIONES LINEALES Ejemplo: Resuelva el siguiente problema de valor inicial lineal: Solución: En primer lugar, la ecuación se escribe en su forma estándar. Luego, como p(x) = 3, el factor integrante es y al multiplicar la ecuación diferencial por m (x)

U-2. CAP. VII. ECUACIONES LINEALES es decir se puede observar que el lado izquierdo de la ecuación corresponde con la derivada del producto e 3 xy Finalmente, la solución general es: o bien

U-2. CAP. VII. ECUACIONES LINEALES Las soluciones de las integrales son: así y aplicando la condición inicial: se obtiene la solución particular:

U-2. CAP. VII. ECUACIONES LINEALES Ejemplo: Resuelva la siguiente ecuación lineal: Solución: La ecuación se escribe en su forma estándar (primero restando 2 y y después dividiendo entre x). de manera que el factor integrante, mediante la aplicación de las propiedades de los logaritmos, resulta en

U-2. CAP. VII. ECUACIONES LINEALES Así, la ecuación diferencial se transforma en Por lo que su solución general se obtiene en la forma que resulta en

U-2. CAP. VII. ECUACIONES LINEALES La solución de una ecuación diferencial lineal de primer orden debe ser general y completa. Suponiendo que se parte de una forma general que incluye las funciones generales p(x) y q(x), cuyo único requisito es que sean continuas, debe ser adecuado asumir que una ecuación lineal de primer orden siempre tiene una solución y que todas las soluciones están incluidas en la ecuación:

U-2. CAP. VII. ECUACIONES LINEALES Estos argumentos se resumen en el teorema de existencia y unicidad de la solución de las ecuaciones diferenciales lineales de primer orden: Si las funciones p(x) y q(x) son continuas en el intervalo abierto I que contiene el punto x 0, entonces la ecuación diferencial lineal de primer orden tiene una solución única en I, dada por

U-2. CAP. VII. ECUACIONES LINEALES El teorema afirma que, bajo condiciones especificas, el problema de valor inicial lineal de primer orden tiene una solución y que ésta es única. Es posible verificar que la ecuación lineal tiene, al menos, una solución mediante su sustitución en la ecuación generadora, para obtener una identidad. Con el valor de la constante C, obtenido a partir de la aplicación de la condición inicial, la solución representa una función única. La solución general incluye todas las soluciones posibles, es decir, la ecuación lineal no tiene una solución singular.
 Ecuaciones lineales objetivos
Ecuaciones lineales objetivos Unidad 4 sistemas de ecuaciones diferenciales lineales
Unidad 4 sistemas de ecuaciones diferenciales lineales Https://slidetodoc.com/captulo-2-o-sudeste-e-o-sul-do/
Https://slidetodoc.com/captulo-2-o-sudeste-e-o-sul-do/ Conceito de judaismo
Conceito de judaismo Sistema de ecuaciones lineales definición
Sistema de ecuaciones lineales definición Que es una ecuacion lineal
Que es una ecuacion lineal Sistemas de ecuaciones lineales
Sistemas de ecuaciones lineales Ecuaciones lineales en los negocios
Ecuaciones lineales en los negocios Sistema de ecuaciones suma y resta
Sistema de ecuaciones suma y resta Sistema de ecuaciones
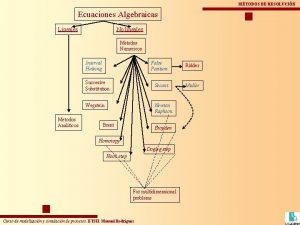
Sistema de ecuaciones Ecuaciones algebraicas
Ecuaciones algebraicas Problemas de ecuaciones diferenciales ordinarias
Problemas de ecuaciones diferenciales ordinarias Ecuaciones condicionales
Ecuaciones condicionales Ecuaciones lineales
Ecuaciones lineales