UNIDAD 12 NDICE OBJETIVO 1 OBJETIVO 2 OBJETIVO

UNIDAD 12

ÍNDICE • • • OBJETIVO 1 OBJETIVO 2 OBJETIVO 3 OBJETIVO 4 OBJETIVO 5 OBJETIVO 6

OBJETIVO 1 ÍNDICE

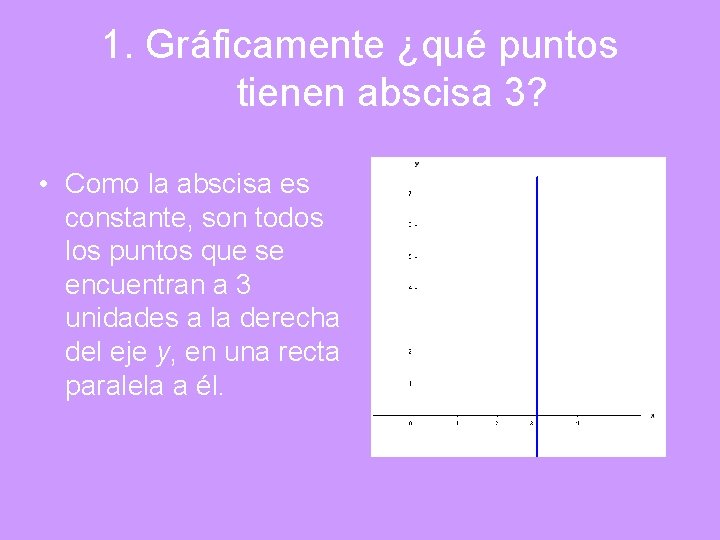
1. Gráficamente ¿qué puntos tienen abscisa 3? • Como la abscisa es constante, son todos los puntos que se encuentran a 3 unidades a la derecha del eje y, en una recta paralela a él.

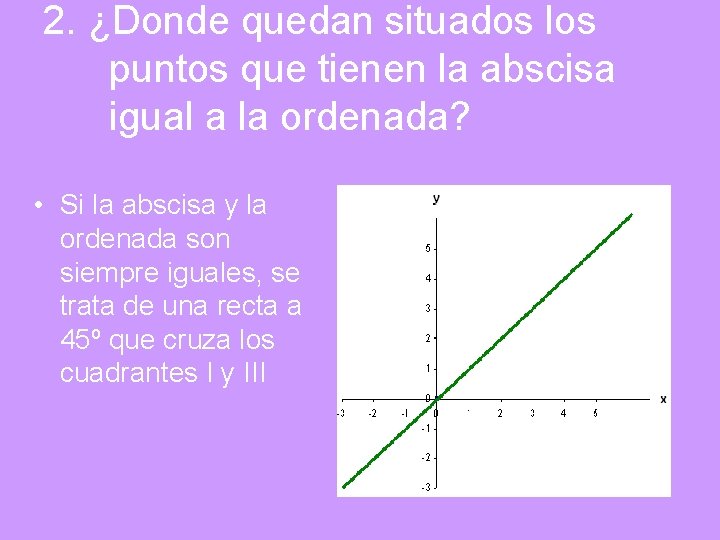
2. ¿Donde quedan situados los puntos que tienen la abscisa igual a la ordenada? • Si la abscisa y la ordenada son siempre iguales, se trata de una recta a 45º que cruza los cuadrantes I y III

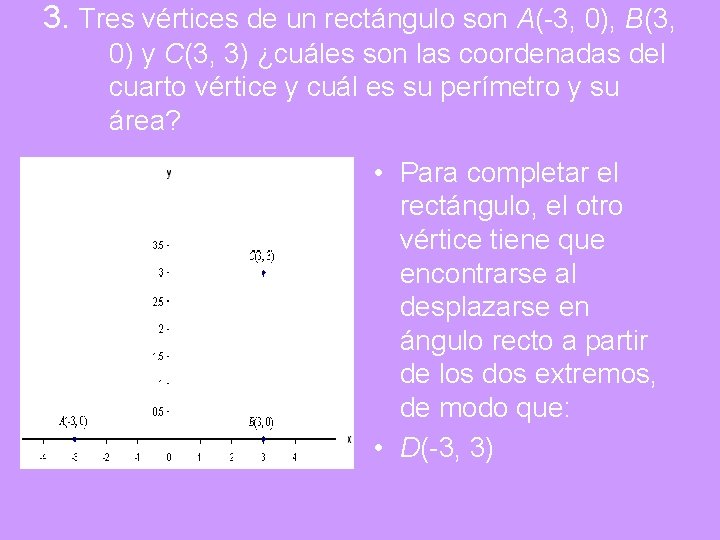
3. Tres vértices de un rectángulo son A(-3, 0), B(3, 0) y C(3, 3) ¿cuáles son las coordenadas del cuarto vértice y cuál es su perímetro y su área? • Para completar el rectángulo, el otro vértice tiene que encontrarse al desplazarse en ángulo recto a partir de los dos extremos, de modo que: • D(-3, 3)

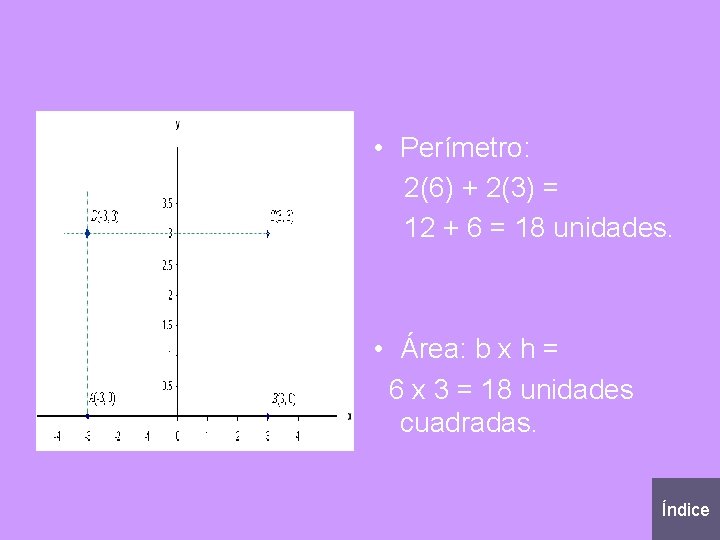
• Perímetro: 2(6) + 2(3) = 12 + 6 = 18 unidades. • Área: b x h = 6 x 3 = 18 unidades cuadradas. Índice

OBJETIVO 2 ÍNDICE

a) Distancia entre dos puntos. 1. Encuentra la distancia del origen al punto A(a, b) SOLUCIÓN:

2. Encuentra el valor de x necesario para que el punto P(x, 3) sea equidistante de los puntos A(3, – 2) y B(7, 4). Para que P equidiste de A de B:

El punto P(2, 3) equidista de los puntos A(3, – 2) y B(7, 4).

3. Si los extremos de un diámetro de una circunferencia son los puntos A(2, 3) y B(5, 8), calcula la longitud de la circunferencia y el área del círculo que limita. Diámetro = Circunferencia = Área del círculo =

b) Coordenadas del punto que divide a un segmento en una razón dada. 1. Si A(2, 3) es un extremo del segmento cuyo punto medio es P(5, 4), encuentra las coordenadas del otro extremo, B.

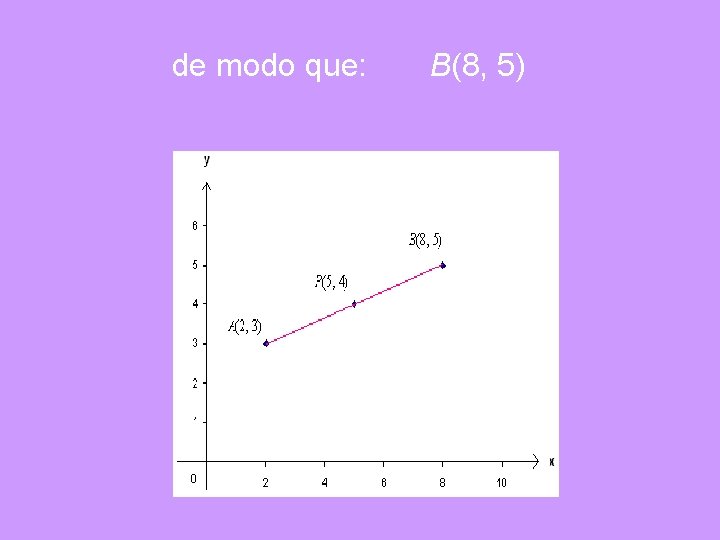
de modo que: B(8, 5)

2. Encuentra la longitud de la mediana del lado del triángulo cuyos vértices son A(– 2, – 2), B(6, 0) y C(2, 8). (La mediana es la recta que une el punto medio de un cateto del triángulo con el vértice opuesto). Coordenadas del punto medio del segmento P(2, -1) Distancia del punto P al vértice C La mediana del cateto al vértice C tiene una longitud de 9 unidades.

3. Los extremos de un segmento son los puntos A(7, 4) y B(-1, -4). Encuentra la razón en que el punto P(1, – 2) divide al segmento. La razón en que el punto P(1, – 2) divide al segmento Índice

OBJETIVO 3 Se aplican los problemas de los objetivos siguientes ÍNDICE

OBJETIVO 4 ÍNDICE

1. Encuentra la ecuación de la recta que pasa por los puntos A(– 2, – 3) y B(5, 1)

2. Encuentra la ecuación de la recta que intersecta al eje de las ordenadas 7 unidades hacia abajo del origen y tiene una pendiente de

3. Tres vértices de un paralelogramo son los puntos A , B(0, 5) y C(– 5, 8). Encuentra las ecuaciones de los lados que pasan por AB y por BC. Ecuación del lado que pasa por A y B: Ecuación del lado que pasa por B y C: B(0, 5); C(– 5, 8)

4. Encuentra la ecuación de una recta perpendicular a eje y, que pase por el punto (h, k) α = 0º; tan α = 0 Índice

OBJETIVO 5 ÍNDICE

1. Determina la posición relativa de las rectas: Para Por lo tanto, las rectas son perpendiculares.

2. Demostrar que las siguientes rectas forman un cuadrado: Posiciones relativas entre las rectas: R 1 y R 3 son paralelas; R 2 y R 4, son paralelas. R 1 es perpendicular con R 2 y con R 4; R 3 es perpendicular con R 2 y con R 4.

• Punto de intersección entre R 1 y R 2:

• Con el mismo procedimiento encuentras que otros puntos de intersección son: R 1 y R 4: P 2(1, – 1) R 3 y R 2: P 3(7, 3) R 3 y R 4: P 4(6, – 2) • También puedes determinar otros punto para graficar: Si x = 3 Si x = – 3 Si x = 8 Si x = 1 y=9 → P 1(3, 9); y=5 → P 2(– 3, 5); y=8 → P 3(8, 8); y = – 1 → P 4(1, – 1)

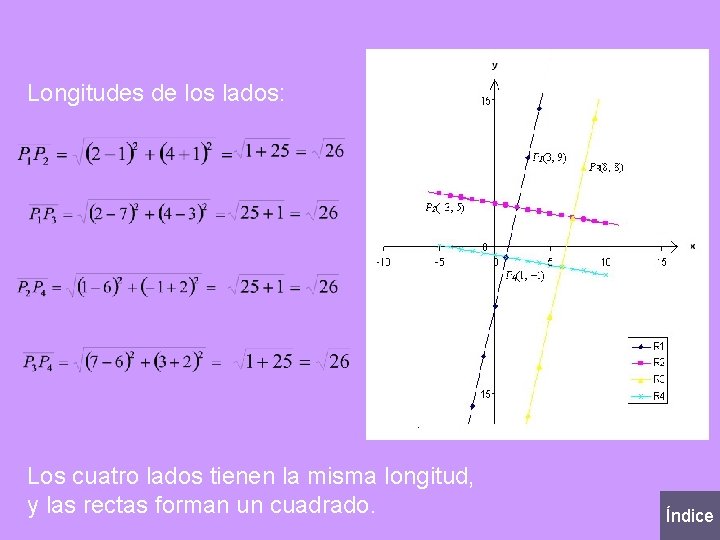
Longitudes de los lados: Los cuatro lados tienen la misma longitud, y las rectas forman un cuadrado. Índice

OBJETIVO 6 ÍNDICE

1. Calcula la longitud del radio de la circunferencia con centro en el punto (2, 3) y que es tangente a la recta Radio de la circunferencia = distancia del centro de la circunferencia a la tangente. radio = 4 (unidades de longitud)

2. Calcula el área del triángulo cuyos vértices son P 1(2, 1), P 2(8, 2) y P 3 (3, 6) Base del triángulo: cualquiera de los tres lados, por ejemplo, Usando la ecuación de la recta que pasa por dos puntos dados:

Longitud de la base: distancia Altura del triángulo: distancia del otro vértice, P 3 (3, 6), a la base:

3. Si la abscisa de P es 2, encuentra su ordenada cuando la distancia dirigida de la recta a un punto P es -3. Distancia dirigida: C<0 signo del radical positivo, y para el punto P (2, y): La ordenada es: y, por tanto: Índice