Uniaxial strain NB Uniaxial strain is a type

Uniaxial strain NB: Uniaxial strain is a type a non-rotational transformation

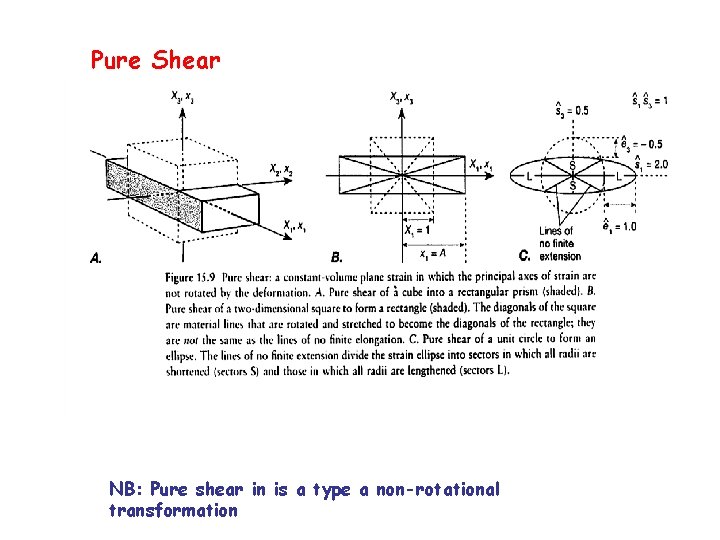
Pure Shear NB: Pure shear in is a type a non-rotational transformation

Simple Shear NB: Simple shear is rotational

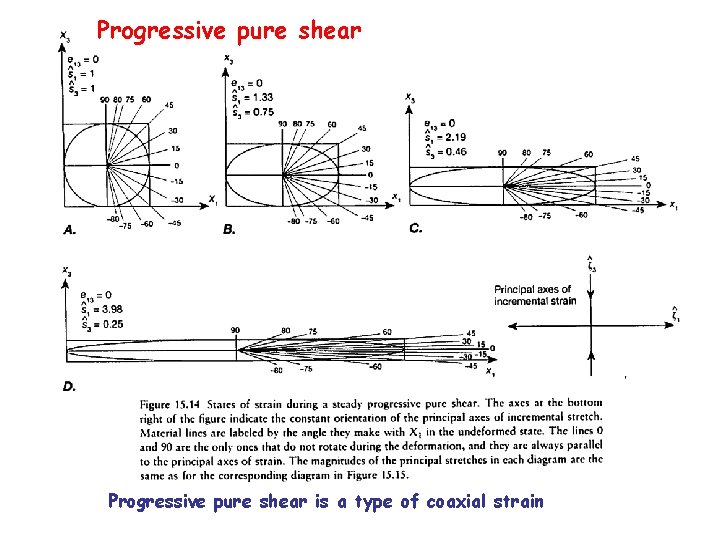
Progressive pure shear is a type of coaxial strain

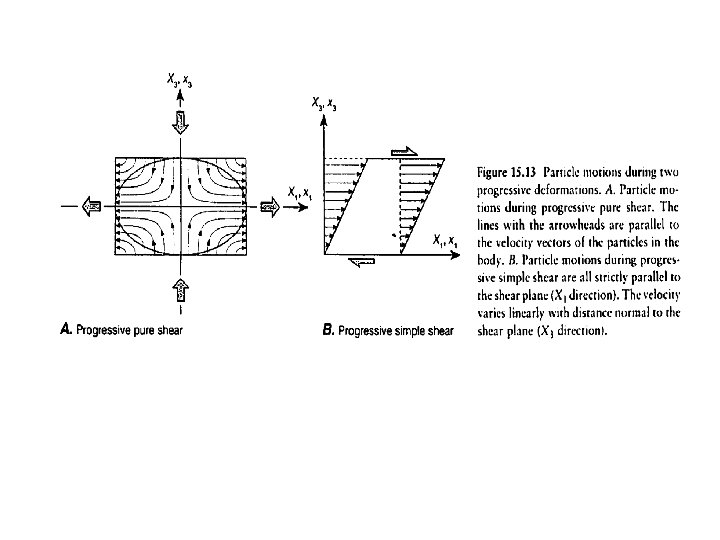
Progressive simple Shear Progressive simple shear is non coaxial

III. Strain and Stress • Strain • Stress • Rheology Reading Suppe, Chapter 3 Twiss&Moores, chapter 15 Additional References : Jean Salençon, Handbook of continuum mechanics: general concepts, thermoelasticity, Springer, 2001 Chandrasekharaiah D. S. , Debnath L. (1994) Continuum Mechanics Publisher: Academic press, Inc.

Stress is force per unit area – Spreading out the weight reduces the stress with the same force. Normal Stress is skier’s weight distributed over skis surface area. F=mg

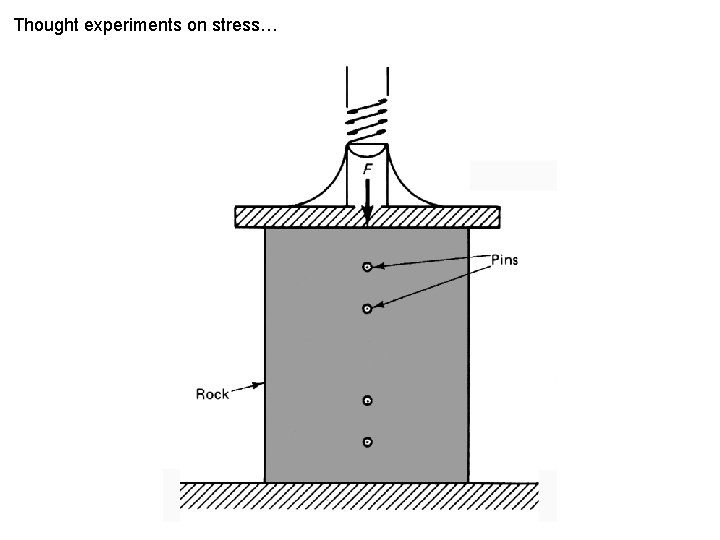
Thought experiments on stress…

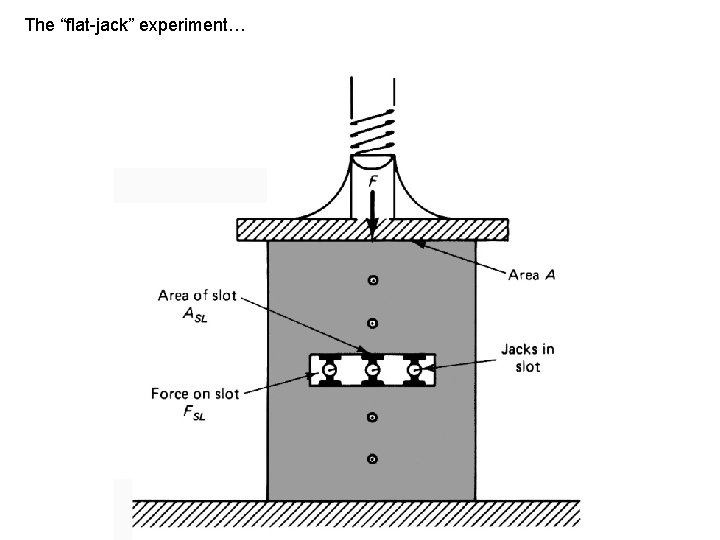
The “flat-jack” experiment…

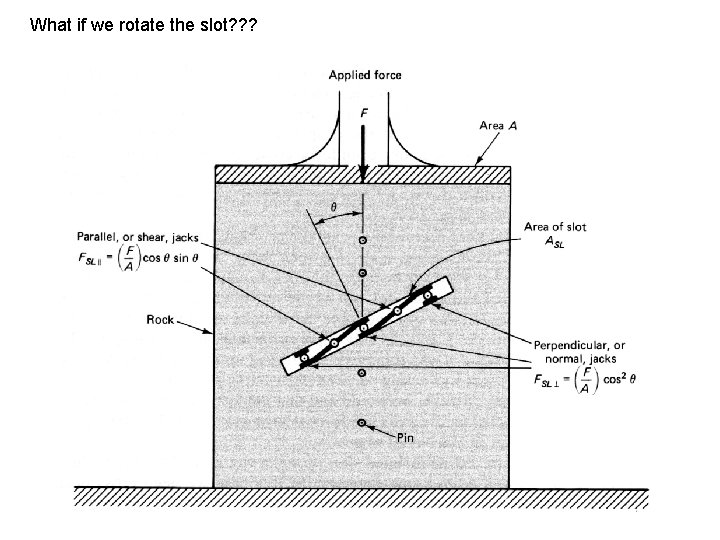
What if we rotate the slot? ? ?

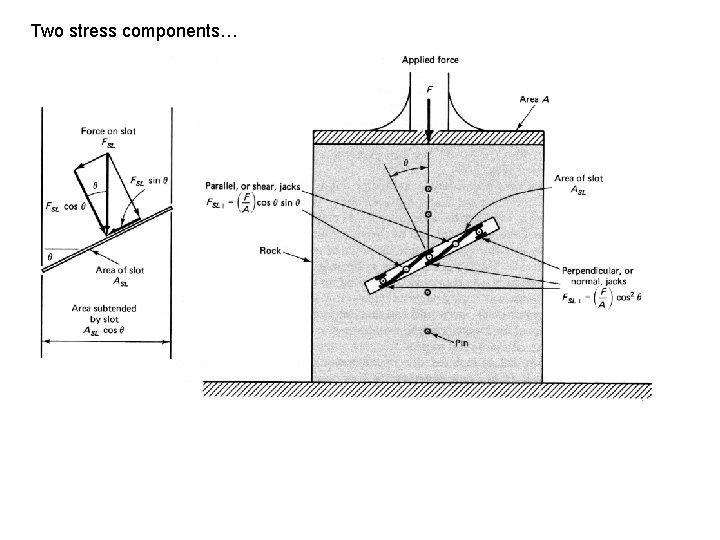
Two stress components…

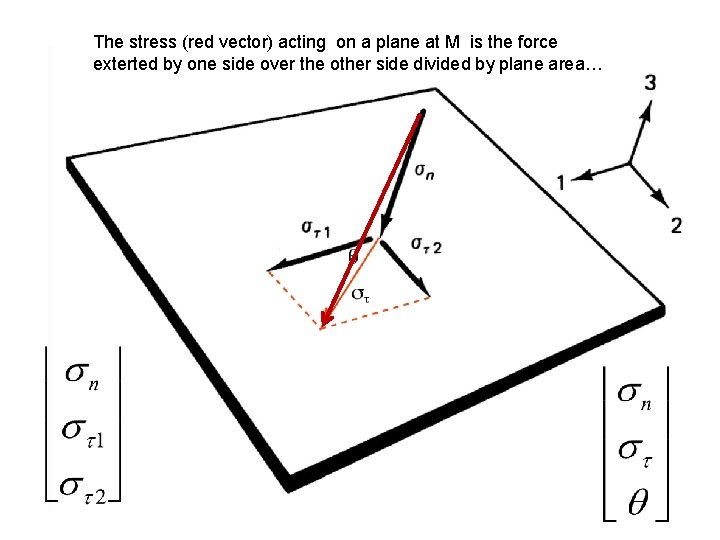
The stress (red vector) acting on a plane at M is the force exterted by one side over the other side divided by plane area…

Stress acting on a plane at point M… Let n be the unit vector defining an oriented surface with elementary area da at point M. (n points from side A to side B) Let d. T be the force exerted on the plane by the medium on side B. It can be decomposed into a normal and shear component parallel to the surface. The stress vector is: Normal stress Shear stress n Side B Side A Convention: positive in compression

The stress tensor The state of stress at a point can be characterizes from the stress tensor defined as …

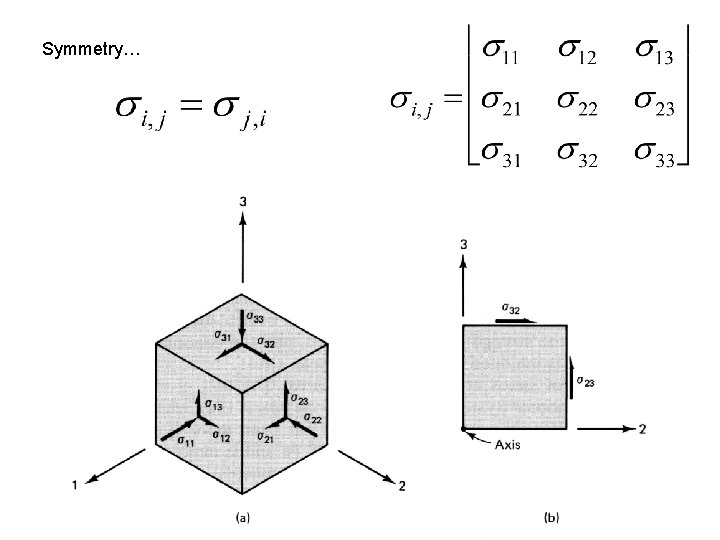
Symmetry…

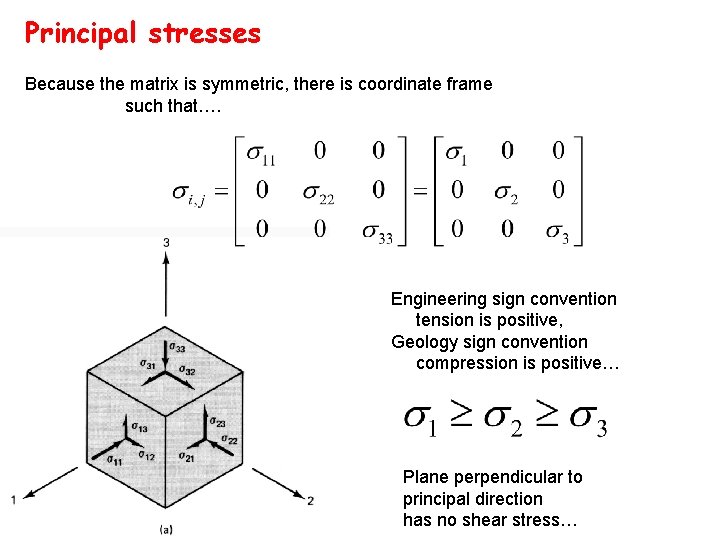
Principal stresses Because the matrix is symmetric, there is coordinate frame such that…. Engineering sign convention tension is positive, Geology sign convention compression is positive… Plane perpendicular to principal direction has no shear stress…

The deviatoric stress tensor… Stress tensor = mean stress + deviatoric stress tensor mean stress: Expressed in a reference frame defined by the principal directions:

Do not confuse the deviatoric stress tensor with the ‘differential stress’, often noted D , defined as

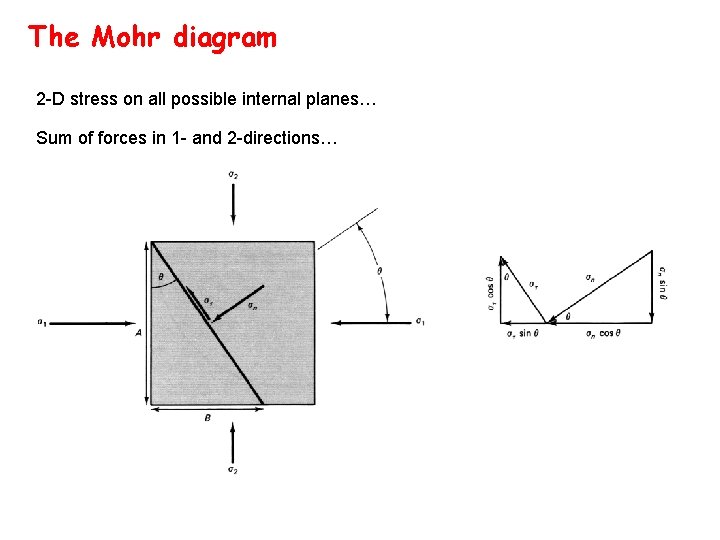
The Mohr diagram 2 -D stress on all possible internal planes… Sum of forces in 1 - and 2 -directions…

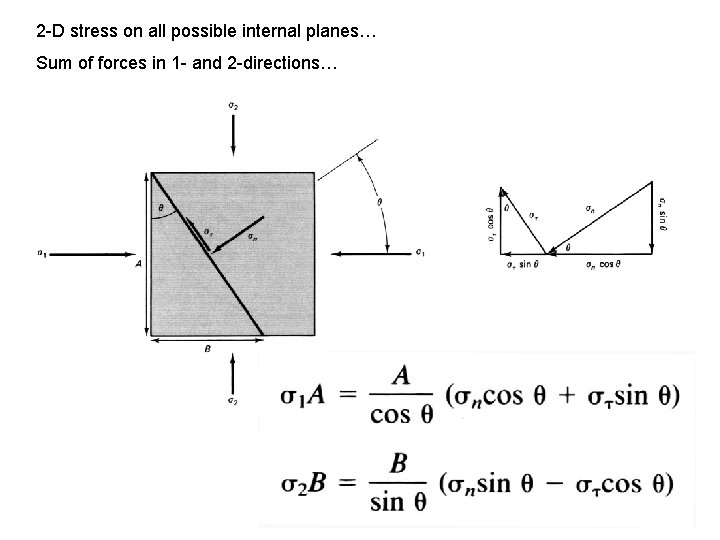
2 -D stress on all possible internal planes… Sum of forces in 1 - and 2 -directions…

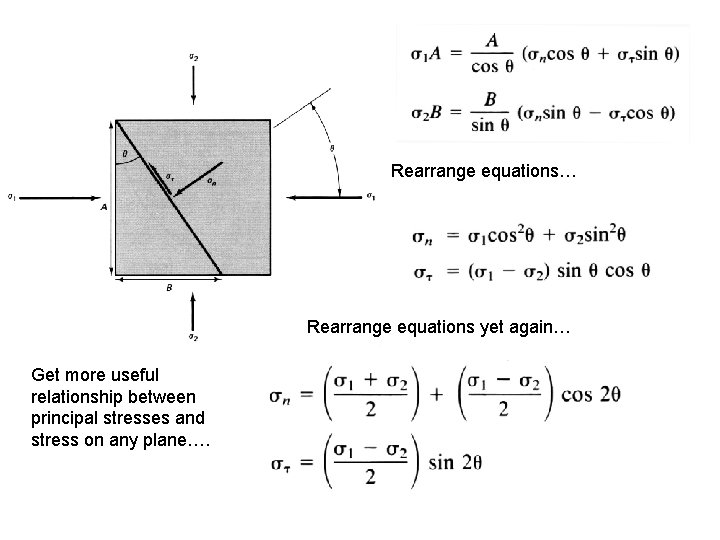
Rearrange equations… Rearrange equations yet again… Get more useful relationship between principal stresses and stress on any plane….

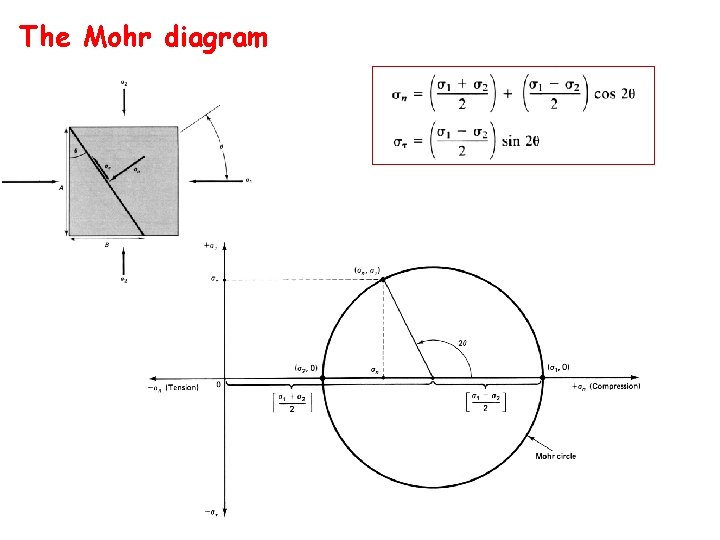
The Mohr diagram

[1] What does a point on the circle mean? Any point on the circle gives coordinates acting on the plane at an angle q to [2] What does the center of the circle tell you? ( is the mean or hydrostatic stress= that which produces change in volume [3] Where are the principle stresses? In direction of and = 0; hence and are on the abscissa axis of Mohr graph [4] What does the diameter or radius mean? ( is the maximum possible shear stress= that which produces change in shape [6] Where is the maximum shear stress? Maximum shear stress max occurs for =45°; then max = (

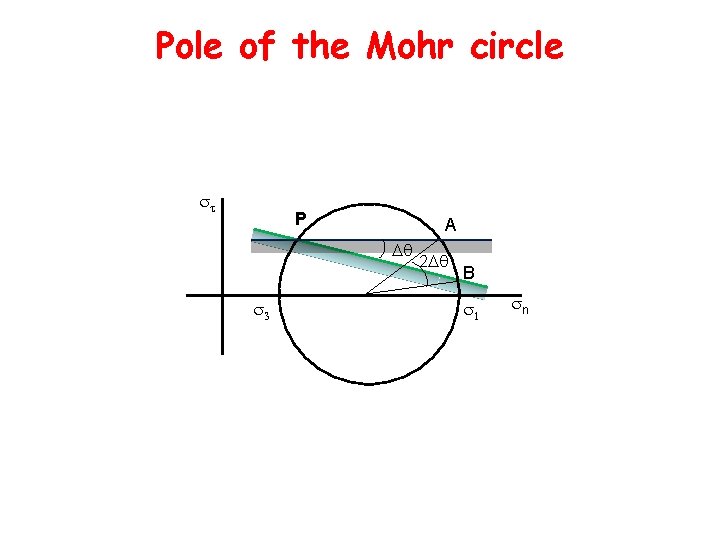
Pole of the Mohr circle P A Dq 2 Dq B n

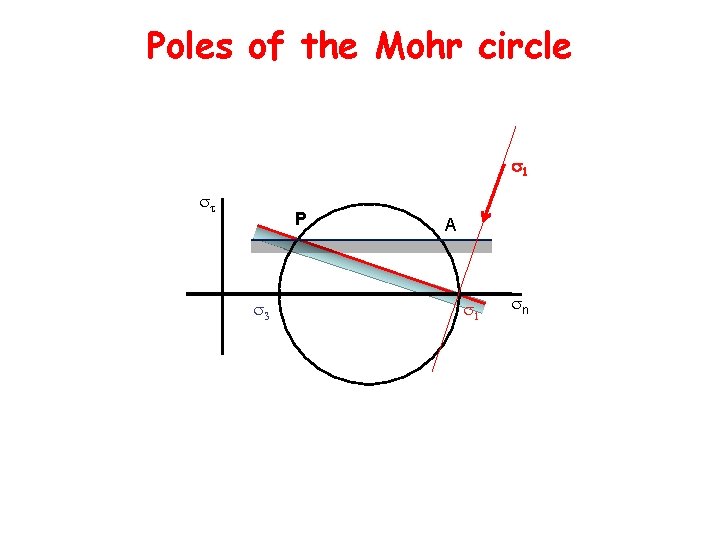
Poles of the Mohr circle 1 P A n

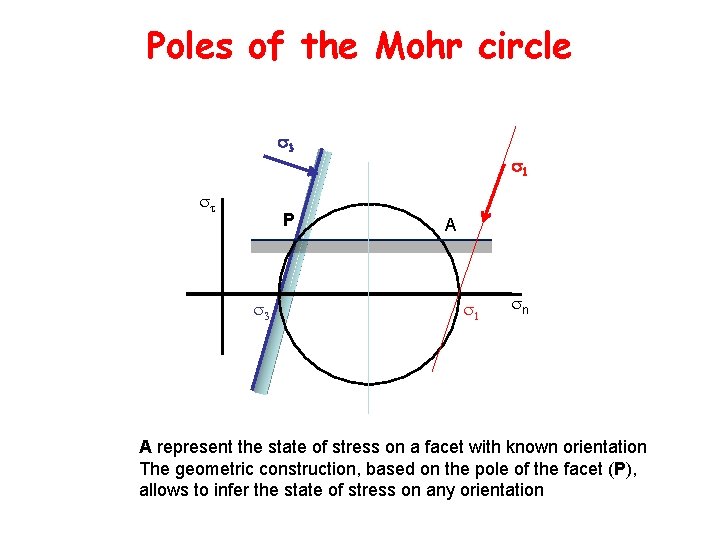
Poles of the Mohr circle 3 P 1 A n A represent the state of stress on a facet with known orientation The geometric construction, based on the pole of the facet (P), allows to infer the state of stress on any orientation

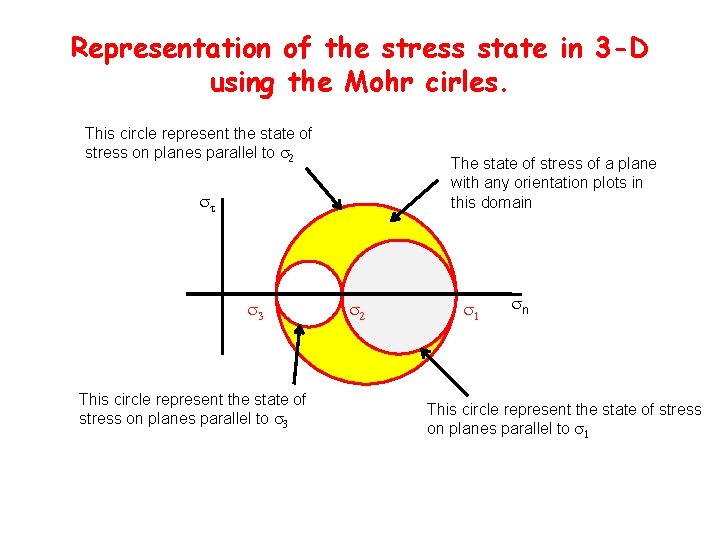
Representation of the stress state in 3 -D using the Mohr cirles. This circle represent the state of stress on planes parallel to The state of stress of a plane with any orientation plots in this domain This circle represent the state of stress on planes parallel to n This circle represent the state of stress on planes parallel to

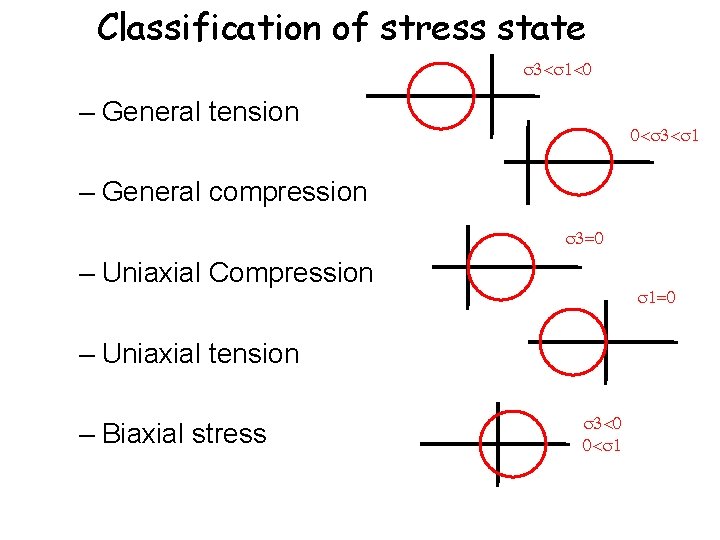
Classification of stress state < <0 – General tension 0< < – General compression =0 – Uniaxial Compression =0 – Uniaxial tension – Biaxial stress <0 0<

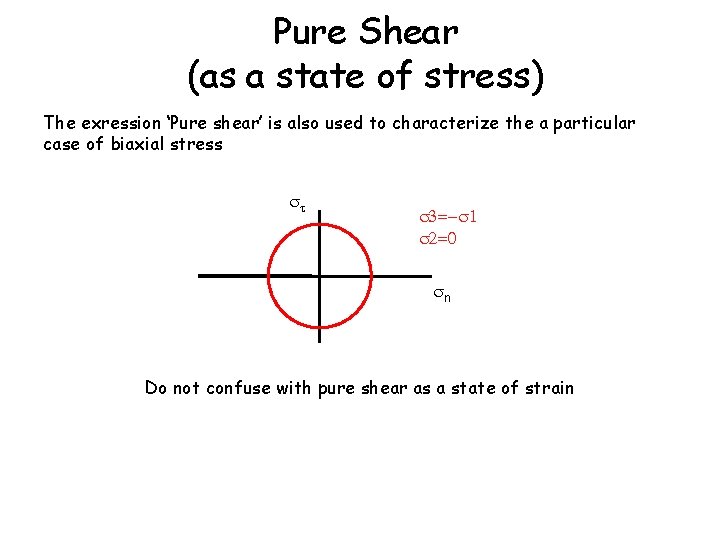
Pure Shear (as a state of stress) The exression ‘Pure shear’ is also used to characterize the a particular case of biaxial stress = =0 n Do not confuse with pure shear as a state of strain

III. Strain and Stress • Strain • Stress • Rheology Reading Suppe, Chapter 3 Twiss&Moores, chapter 15 Additional References : Jean Salençon, Handbook of continuum mechanics: general concepts, thermoelasticity, Springer, 2001 Chandrasekharaiah D. S. , Debnath L. (1994) Continuum Mechanics Publisher: Academic press, Inc.

• A rheological law relates strain to stress and time.

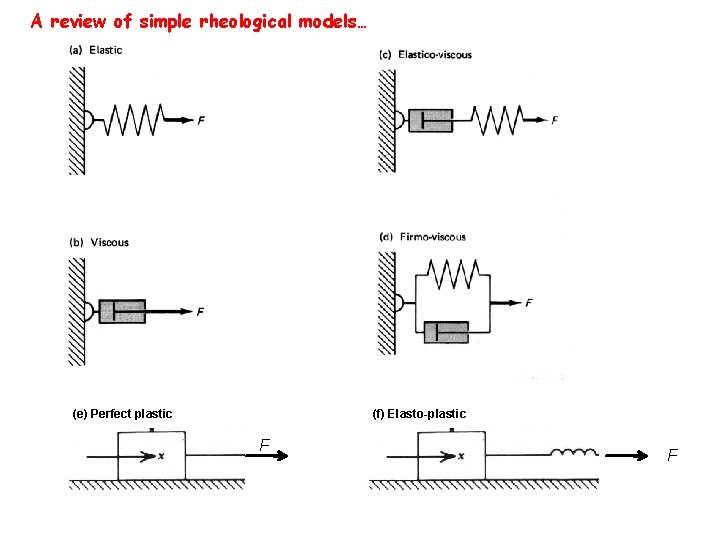
A review of simple rheological models… (e) Perfect plastic (f) Elasto-plastic F F

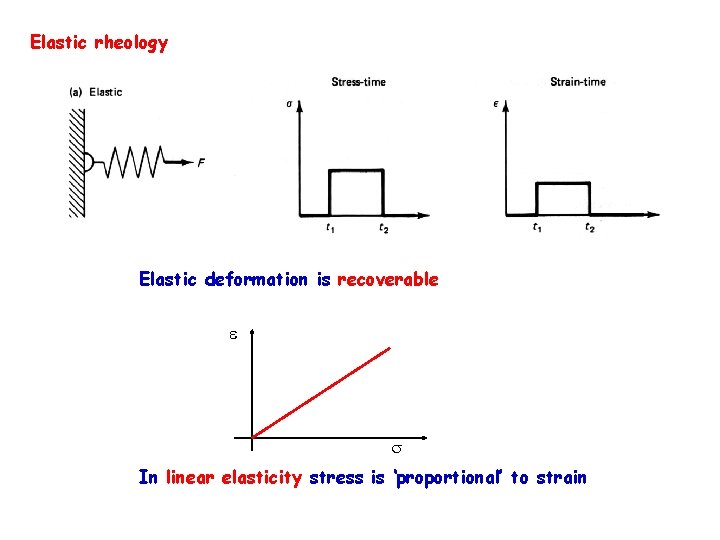
Elastic rheology Elastic deformation is recoverable e In linear elasticity stress is ‘proportional’ to strain

Elastic rheology In linear elasticity stress is ‘proportional’ to stress (‘Hooke’s law’) e is the elasticity tensor. It is a symmetric tensor (21 elasticity coefficients) For an isotropic linear elastic medium there are only 2 elasticity coefficients , e. g. : the Young modulus and Poisson ratio: Shear modulus Young Modulus Poisson ratio Bulk modulus

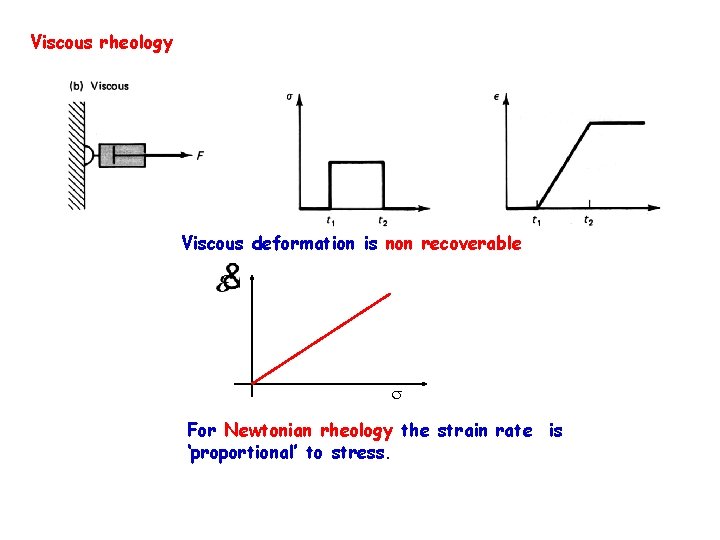
Viscous rheology Viscous deformation is non recoverable For Newtonian rheology the strain rate is ‘proportional’ to stress.

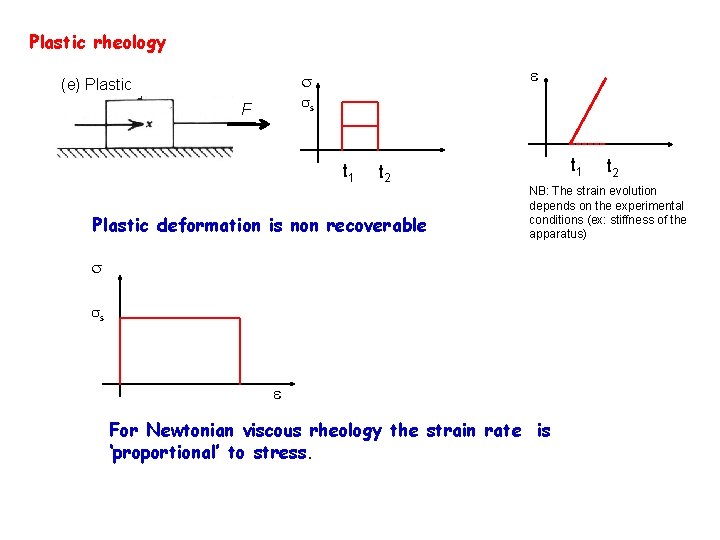
Plastic rheology e (e) Plastic s F t 1 t 2 Plastic deformation is non recoverable t 1 t 2 NB: The strain evolution depends on the experimental conditions (ex: stiffness of the apparatus) s e For Newtonian viscous rheology the strain rate is ‘proportional’ to stress.

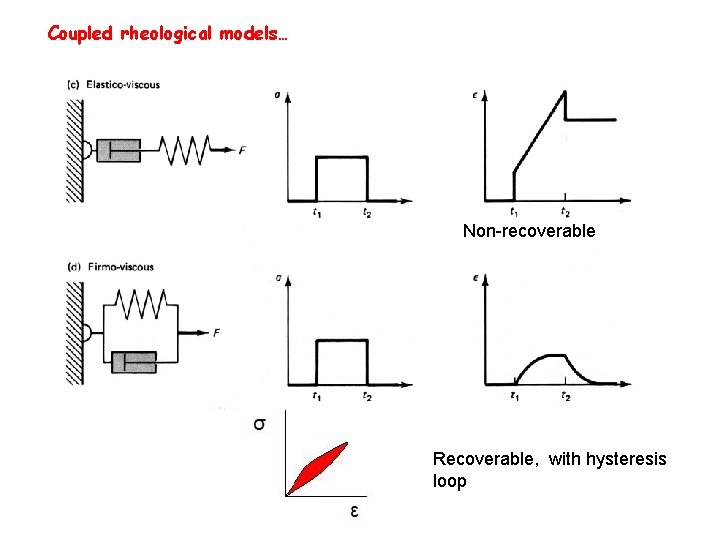
Coupled rheological models… Non-recoverable Recoverable, with hysteresis loop

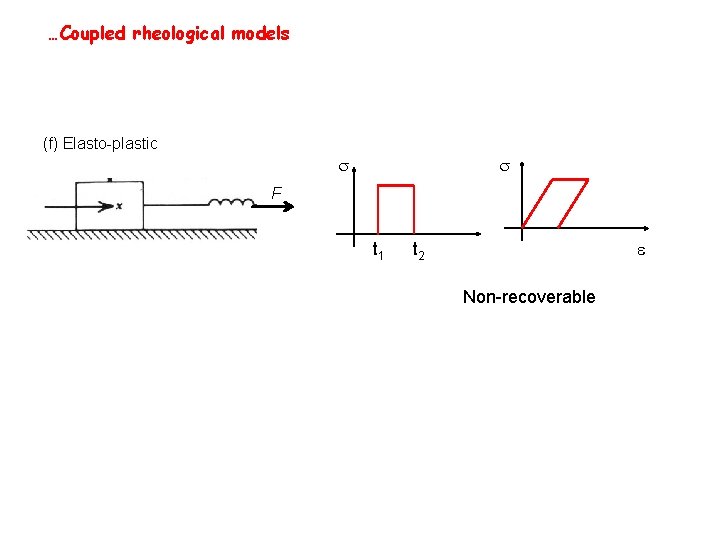
…Coupled rheological models (f) Elasto-plastic F t 1 e t 2 Non-recoverable