Une dmonstration Utiliser les transformations tude de figures

Une démonstration Utiliser les transformations (étude de figures). Figure 1 : Symétrie centrale Figure 2 : Symétrie axiale Figure 3 : Translation Démontrer

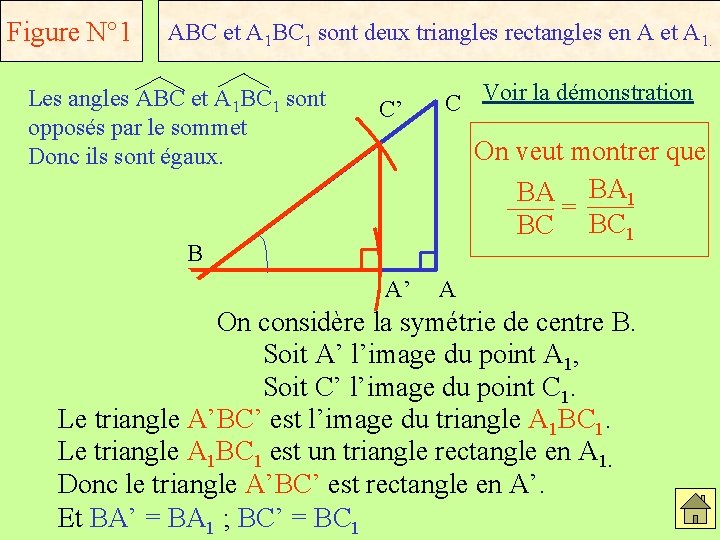
Figure N° 1 ABC et A 1 BC 1 sont deux triangles rectangles en A et A 1. Les angles ABC et A 1 BC 1 sont opposés par le sommet Donc ils sont égaux. A 1 C’ C Voir la démonstration On veut montrer que BA BA 1 = BC BC 1 B A’ A On considère la symétrie de centre B. Soit A’ l’image du point A 1, Soit C’ l’image du point C 1 Le triangle A’BC’ est l’image du triangle A BC. 1 1 Le triangle A 1 BC 1 est un triangle rectangle en A 1. Donc le triangle A’BC’ est rectangle en A’. Et BA’ = BA 1 ; BC’ = BC 1

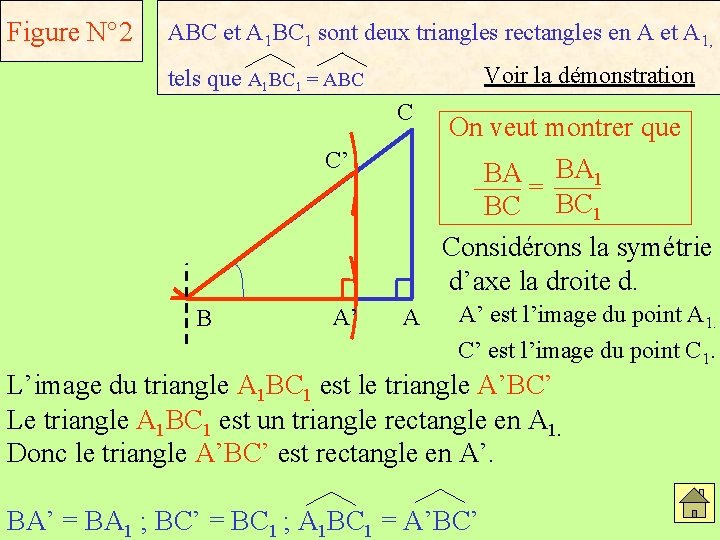
Figure N° 2 ABC et A 1 BC 1 sont deux triangles rectangles en A et A 1, Voir la démonstration tels que A 1 BC 1 = ABC C C 1 A 1 d B C’ A’ On veut montrer que BA BA 1 = BC BC 1 Considérons la symétrie d’axe la droite d. A A’ est l’image du point A 1. C’ est l’image du point C 1. L’image du triangle A 1 BC 1 est le triangle A’BC’ Le triangle A 1 BC 1 est un triangle rectangle en A 1. Donc le triangle A’BC’ est rectangle en A’. BA’ = BA 1 ; BC’ = BC 1 ; A 1 BC 1 = A’BC’

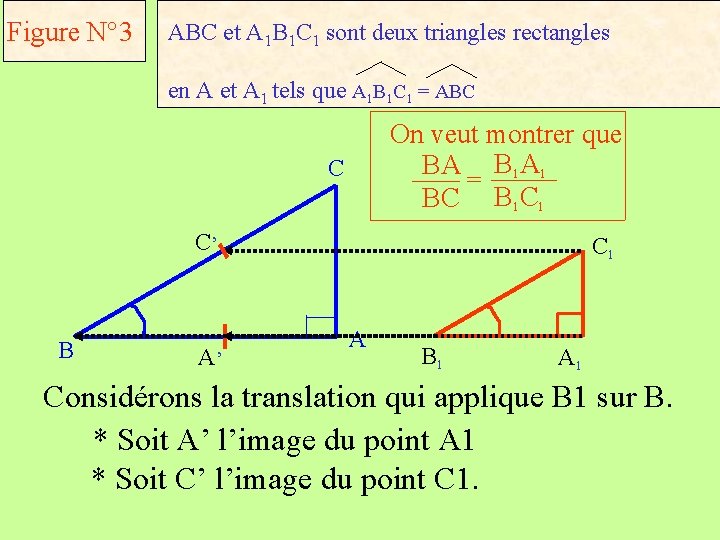
Figure N° 3 ABC et A 1 B 1 C 1 sont deux triangles rectangles en A et A 1 tels que A 1 B 1 C 1 = ABC On veut montrer que BA B 1 A 1 = BC B 1 C 1 C C’ B A’ C 1 A B 1 A 1 Considérons la translation qui applique B 1 sur B. * Soit A’ l’image du point A 1 * Soit C’ l’image du point C 1.

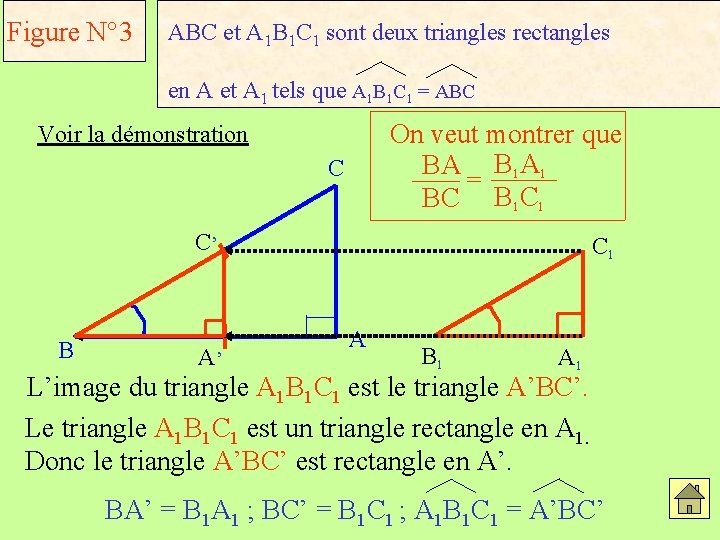
Figure N° 3 ABC et A 1 B 1 C 1 sont deux triangles rectangles en A et A 1 tels que A 1 B 1 C 1 = ABC On veut montrer que BA B 1 A 1 = BC B 1 C 1 Voir la démonstration C C’ B A’ C 1 A B 1 A 1 L’image du triangle A 1 B 1 C 1 est le triangle A’BC’. Le triangle A 1 B 1 C 1 est un triangle rectangle en A 1. Donc le triangle A’BC’ est rectangle en A’. BA’ = B 1 A 1 ; BC’ = B 1 C 1 ; A 1 B 1 C 1 = A’BC’

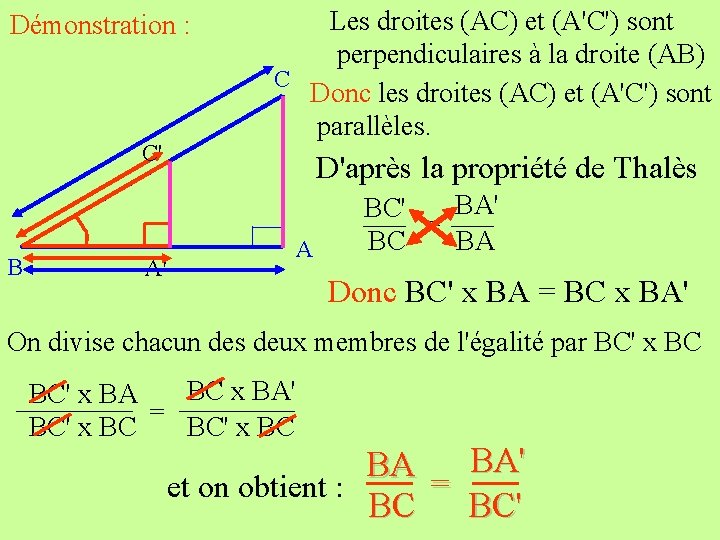
Démonstration : C' B A' Les droites (AC) et (A'C') sont perpendiculaires à la droite (AB) C Donc les droites (AC) et (A'C') sont parallèles. D'après la propriété de Thalès A BA' BC' = BC BA Donc BC' x BA = BC x BA' On divise chacun des deux membres de l'égalité par BC' x BC BC x BA' BC' x BA = BC' x BC BA' BA = et on obtient : BC BC'

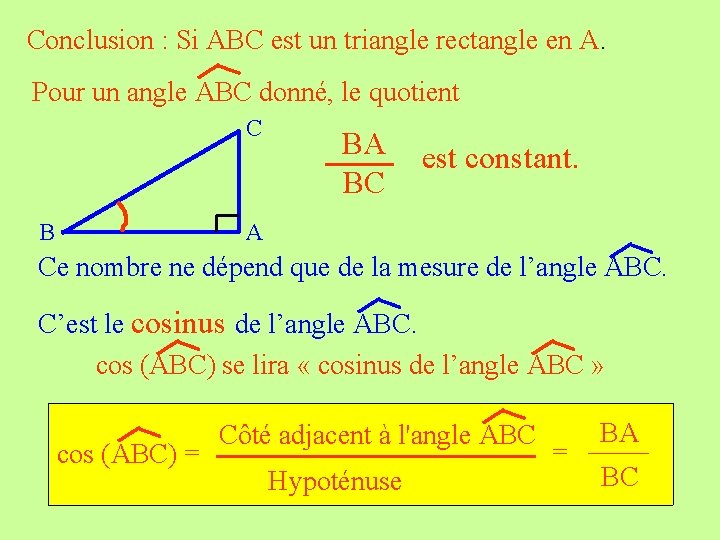
Conclusion : Si ABC est un triangle rectangle en A. Pour un angle ABC donné, le quotient C B BA BC est constant. A Ce nombre ne dépend que de la mesure de l’angle ABC. C’est le cosinus de l’angle ABC. cos (ABC) se lira « cosinus de l’angle ABC » cos (ABC) = Côté adjacent à l'angle ABC Hypoténuse = BA BC

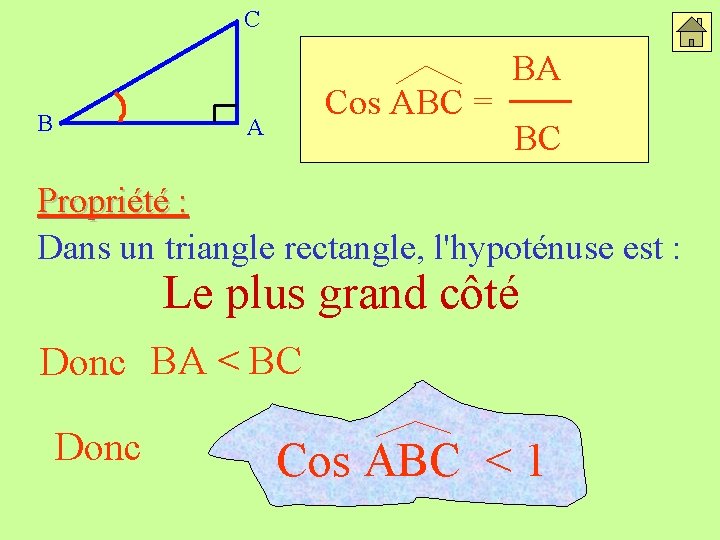
C B Cos ABC = A BA BC Propriété : Dans un triangle rectangle, l'hypoténuse est : Le plus grand côté Donc BA < BC Donc Cos ABC < 1