Understanding Piezo based Sensors for an acoustic neutrino

Understanding Piezo based Sensors for an acoustic neutrino detector ARENA-06, Newcastle, UK Christopher Naumann, Universität Erlangen-Nürnberg

Acoustic Detection with the ANTARES Telescope re-fit several ANTARES storeys with acoustics hardware (sensors and DAQ) Aims: replace optical sensors with acoustic sensors (schematic) -design studies for an acoustic neutrino detector in the deep sea -thorough studies of the acoustic environment in the deep sea: Correlations of the acoustic background over several length scales (<1 m up to > 100 m) ARENA Workshop 2006, Newcastle Christopher Naumann

Aim: Acoustic Sensors • Basic Design of Sensors for the ANTARES acoustics cable internal pre-amplifier ANTARES glass sphere 17" (42 cm) – Sensor = piezo element (disc and/or tube) + pre-amplifier – either encapsulated in polyurethane = > "hydrophone" – or coupled to ANTARES glass sphere = > "acoustic module" piezo tube PU coating piezo sensors + pre-amplifiers Signal response and noise characteristics of sensors depend on piezo element try to build model ARENA Workshop 2006, Newcastle Christopher Naumann

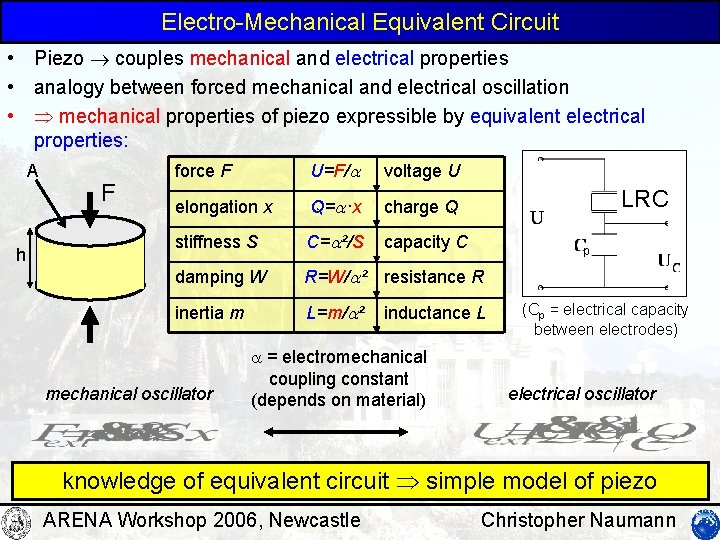
Electro-Mechanical Equivalent Circuit • Piezo couples mechanical and electrical properties • analogy between forced mechanical and electrical oscillation • mechanical properties of piezo expressible by equivalent electrical properties: A h F force F U=F/ voltage U elongation x Q= ·x charge Q stiffness S C= ²/S capacity C damping W R=W/ ² resistance R inertia m L=m/ ² mechanical oscillator LRC p inductance L = electromechanical coupling constant (depends on material) (Cp = electrical capacity between electrodes) electrical oscillator knowledge of equivalent circuit simple model of piezo ARENA Workshop 2006, Newcastle Christopher Naumann

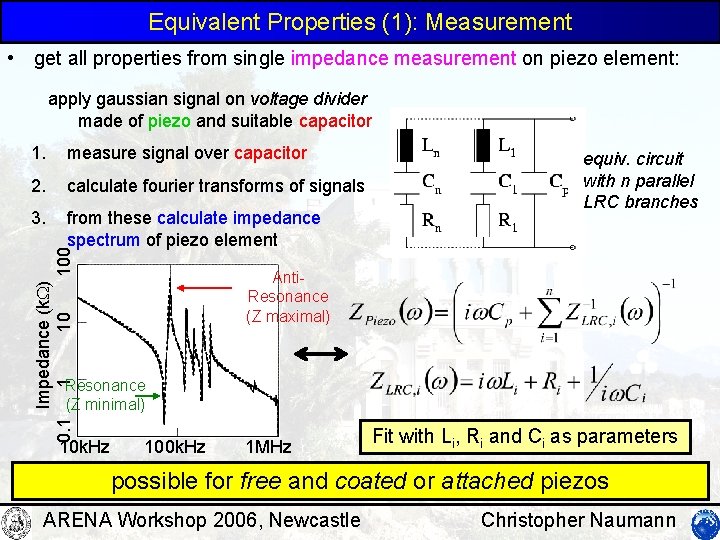
Equivalent Properties (1): Measurement • get all properties from single impedance measurement on piezo element: apply gaussian signal on voltage divider made of piezo and suitable capacitor measure signal over capacitor 2. calculate fourier transforms of signals 3. from these calculate impedance spectrum of piezo element Impedance (k ) 0. 1 1 10 100 1. equiv. circuit with n parallel LRC branches Anti. Resonance (Z maximal) Resonance (Z minimal) 10 k. Hz 100 k. Hz 1 MHz Fit with Li, Ri and Ci as parameters possible for free and coated or attached piezos ARENA Workshop 2006, Newcastle Christopher Naumann

Equivalent Properties (2): Coupling Properties of piezo elements depend on coupling to environment: coupling limits movement damping R increases resonances are weakened - other properties unchanged free piezo 74 m. H 666 25 p. F Impedance (k ) 0. 1 1 10 100 free piezo: strong resonances coupled: resonances suppressed 10 k. Hz piezo in sphere 74 m. H 3043 23 p. F 100 k. Hz 1 MHz Frequency sensitivity of piezo element can now be modelled. . . significant increase of equivalent ohmic resistance damping ARENA Workshop 2006, Newcastle Christopher Naumann

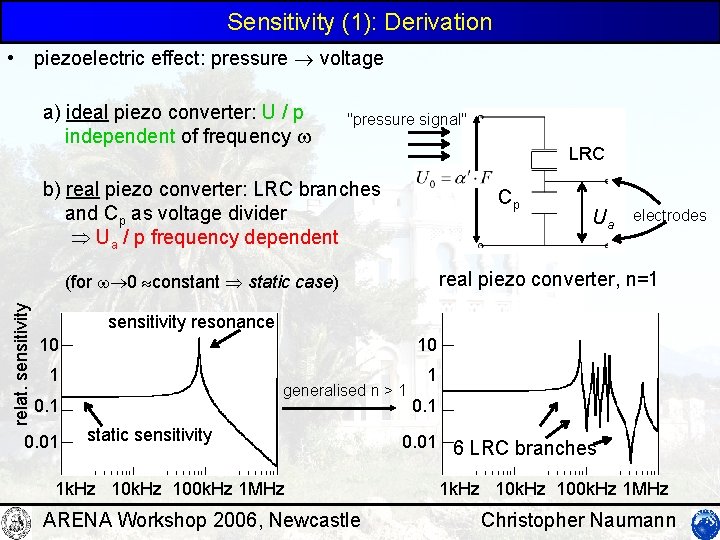
Sensitivity (1): Derivation • piezoelectric effect: pressure voltage a) ideal piezo converter: U / p independent of frequency "pressure signal" LRC b) real piezo converter: LRC branches and Cp as voltage divider Ua / p frequency dependent Cp electrodes real piezo converter, n=1 (for 0 constant static case) relat. sensitivity Ua sensitivity resonance 10 10 1 generalised n > 1 0. 01 static sensitivity 1 k. Hz 100 k. Hz 1 MHz ARENA Workshop 2006, Newcastle 1 0. 01 6 LRC branches 1 k. Hz 100 k. Hz 1 MHz Christopher Naumann

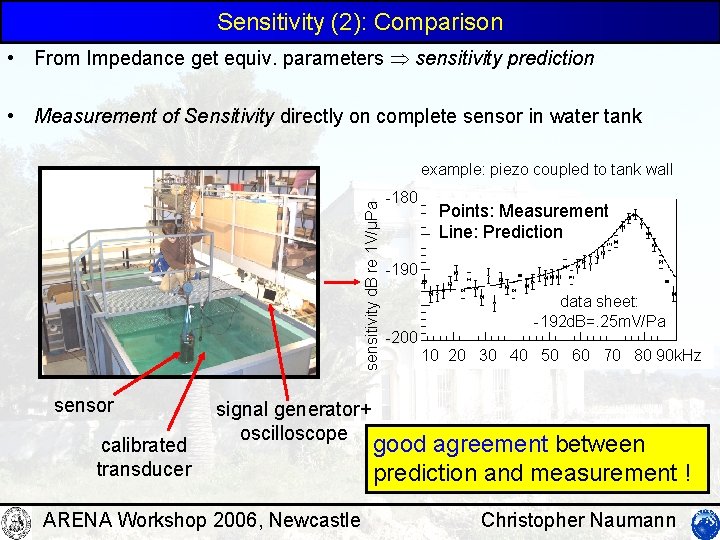
Sensitivity (2): Comparison • From Impedance get equiv. parameters sensitivity prediction • Measurement of Sensitivity directly on complete sensor in water tank sensitivity d. B re 1 V/µPa example: piezo coupled to tank wall sensor calibrated transducer signal generator+ oscilloscope ARENA Workshop 2006, Newcastle -180 Points: Measurement Line: Prediction -190 -200 data sheet: -192 d. B=. 25 m. V/Pa 10 20 30 40 50 60 70 80 90 k. Hz good agreement between prediction and measurement ! Christopher Naumann

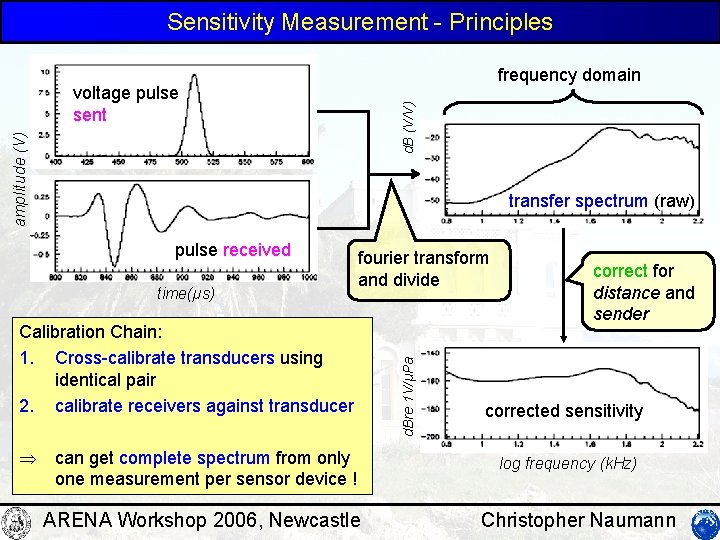
Sensitivity Measurement - Principles frequency domain amplitude (V) d. B (V/V) voltage pulse sent transfer spectrum (raw) time(µs) fourier transform and divide Calibration Chain: 1. Cross-calibrate transducers using identical pair 2. calibrate receivers against transducer can get complete spectrum from only one measurement per sensor device ! ARENA Workshop 2006, Newcastle d. Bre 1 V/µPa pulse received correct for distance and sender corrected sensitivity log frequency (k. Hz) Christopher Naumann

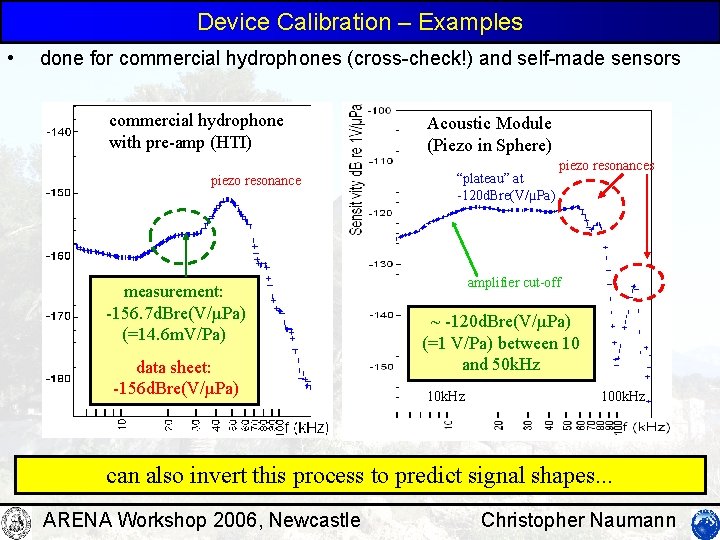
Device Calibration – Examples • done for commercial hydrophones (cross-check!) and self-made sensors commercial hydrophone with pre-amp (HTI) piezo resonance measurement: -156. 7 d. Bre(V/µPa) (=14. 6 m. V/Pa) data sheet: -156 d. Bre(V/µPa) Acoustic Module (Piezo in Sphere) “plateau” at -120 d. Bre(V/µPa) piezo resonances amplifier cut-off ~ -120 d. Bre(V/µPa) (=1 V/Pa) between 10 and 50 k. Hz 100 k. Hz can also invert this process to predict signal shapes. . . ARENA Workshop 2006, Newcastle Christopher Naumann

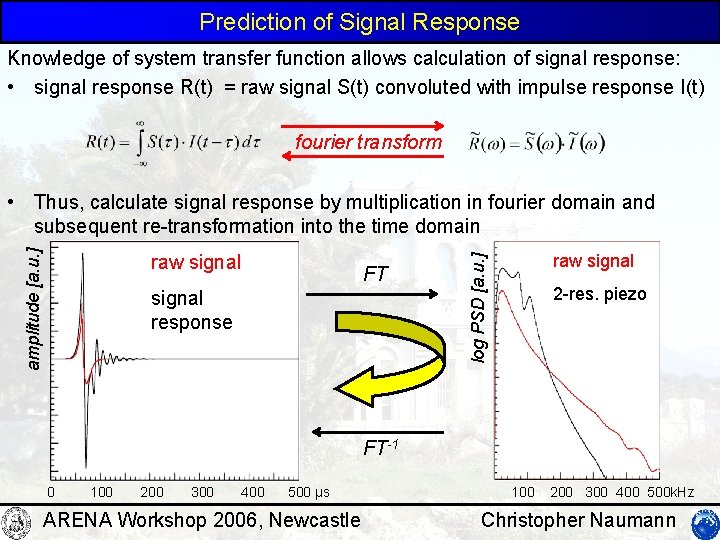
Prediction of Signal Response Knowledge of system transfer function allows calculation of signal response: • signal response R(t) = raw signal S(t) convoluted with impulse response I(t) fourier transform raw signal FT signal response raw signal log PSD [a. u. ] amplitude [a. u. ] • Thus, calculate signal response by multiplication in fourier domain and subsequent re-transformation into the time domain 2 -res. piezo FT-1 0 100 200 300 400 500 µs ARENA Workshop 2006, Newcastle 100 200 300 400 500 k. Hz Christopher Naumann

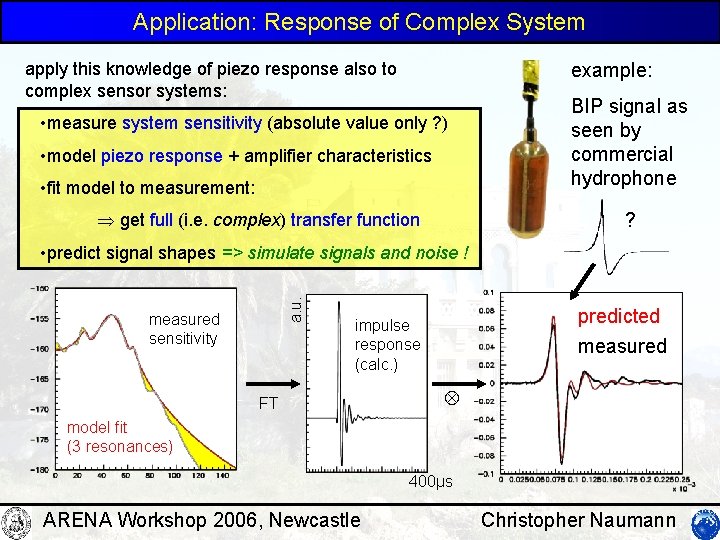
Application: Response of Complex System apply this knowledge of piezo response also to complex sensor systems: example: • measure system sensitivity (absolute value only ? ) • model piezo response + amplifier characteristics • fit model to measurement: get full (i. e. complex) transfer function BIP signal as seen by commercial hydrophone ? a. u. • predict signal shapes => simulate signals and noise ! measured sensitivity predicted measured impulse response (calc. ) FT model fit (3 resonances) 400µs ARENA Workshop 2006, Newcastle Christopher Naumann

Model Predictions (2) – Piezo Elongation • inverse piezoelectric effect: applied voltage U = > elongation x (important e. g. for acoustic senders) coupling: current <-> velocity: displacement proportional to integral over voltage for sine signal, frequency : =displacement averaged over face of piezo applicable to arbitrary signals by fourier analysis behaviour for 0: see Karsten's talk tomorrow static case x= U/s ARENA Workshop 2006, Newcastle Christopher Naumann

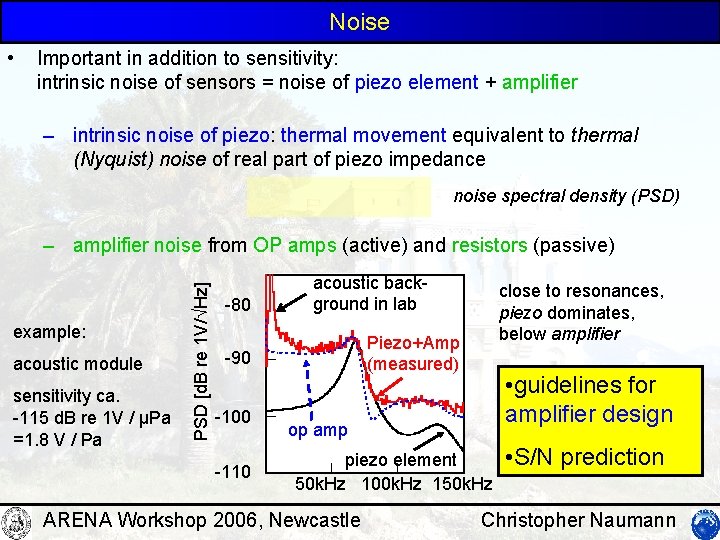
Noise • Important in addition to sensitivity: intrinsic noise of sensors = noise of piezo element + amplifier – intrinsic noise of piezo: thermal movement equivalent to thermal (Nyquist) noise of real part of piezo impedance noise spectral density (PSD) example: acoustic module sensitivity ca. -115 d. B re 1 V / µPa =1. 8 V / Pa PSD [d. B re 1 V/ Hz] – amplifier noise from OP amps (active) and resistors (passive) -80 acoustic background in lab Piezo+Amp (measured) -90 -100 -110 close to resonances, piezo dominates, below amplifier • guidelines for amplifier design op amp piezo element 50 k. Hz 100 k. Hz 150 k. Hz ARENA Workshop 2006, Newcastle • S/N prediction Christopher Naumann

Conclusions and Outlook • Achievements: – easy description of piezo sensors by electromechanical equivalent properties possible – Acquisition of equivalent parameters by impedance measurement (also for coupled or coated piezo elements) – very good agreement between model predictions and measurements for sensitivity, displacement and noise – possibility to model signal response • Outlook: – use this knowledge to design and build acoustic storeys for ANTARES for operation in the deep sea ! – do extensive simulation / reconstruction studies using realistic system response Thank you for your attention ! ARENA Workshop 2006, Newcastle Christopher Naumann