Understanding Graphs CHAPTER 1 Appendix Graph Picture showing

Understanding Graphs CHAPTER 1 Appendix

Graph Picture showing how variables relate and conveys information in a compact and efficient way Functional relation exists between two variables when the value of one variable depends on another The value of the dependent variable depends on the value of the independent variable

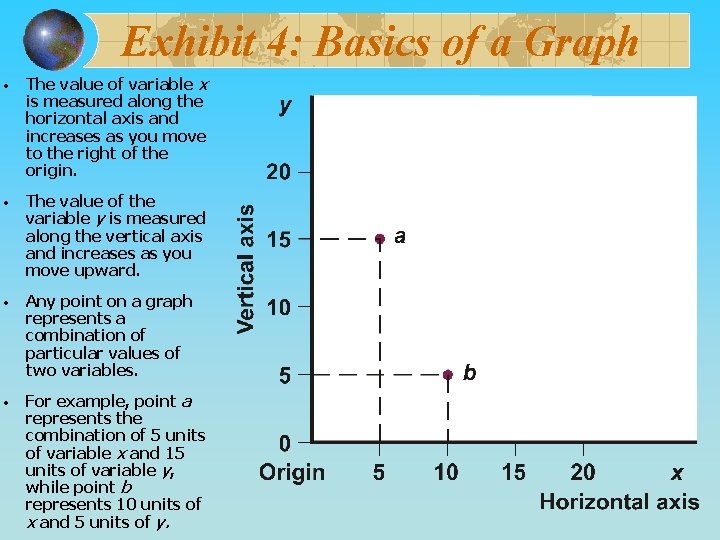
Exhibit 4: Basics of a Graph • The value of variable x is measured along the horizontal axis and increases as you move to the right of the origin. • The value of the variable y is measured along the vertical axis and increases as you move upward. • Any point on a graph represents a combination of particular values of two variables. • For example, point a represents the combination of 5 units of variable x and 15 units of variable y, while point b represents 10 units of x and 5 units of y.

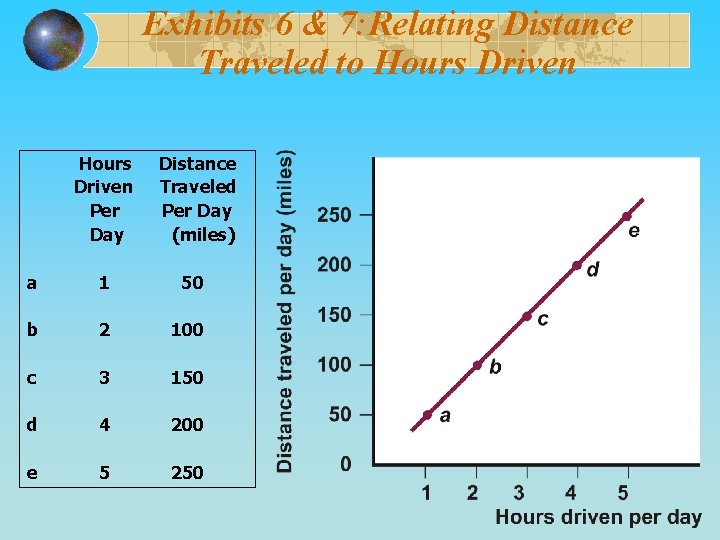
Exhibits 6 & 7: Relating Distance Traveled to Hours Driven Per Day Distance Traveled Per Day (miles) a 1 50 b 2 100 c 3 150 d 4 200 e 5 250

Slopes of Straight Lines Indicates how much the vertical variable changes for a given change in the horizontal variable Vertical Change divided by the horizontal Change Slope = Change in the vertical distance / change in the horizontal distance

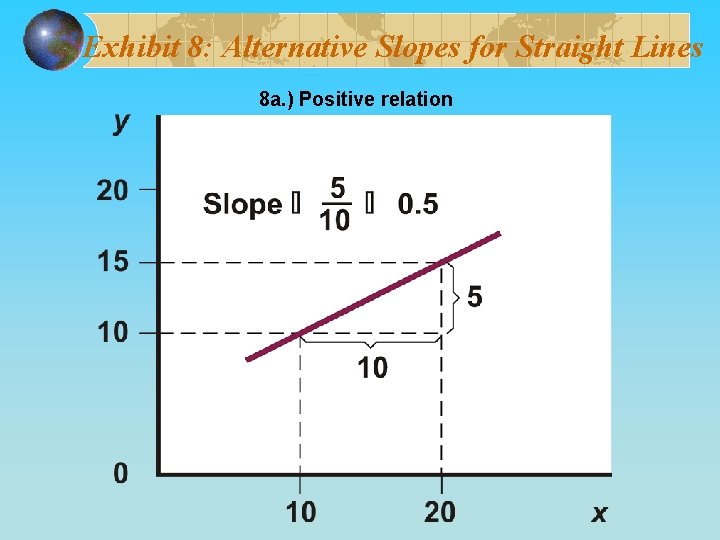
Exhibit 8: Alternative Slopes for Straight Lines 8 a. ) Positive relation

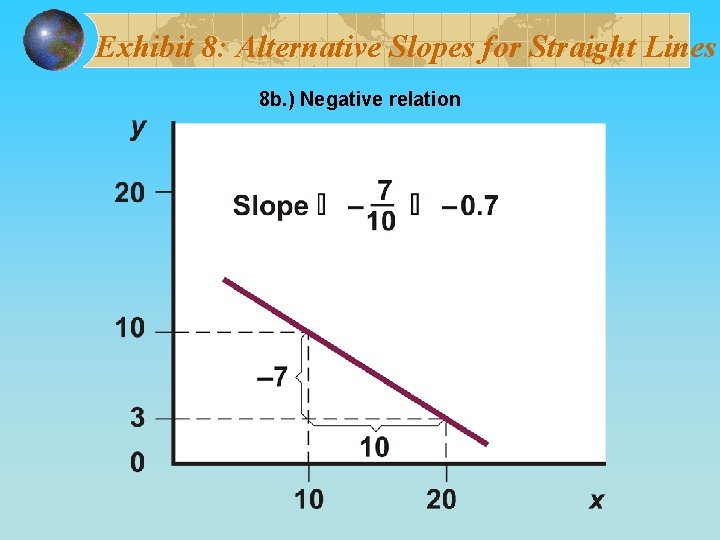
Exhibit 8: Alternative Slopes for Straight Lines 8 b. ) Negative relation

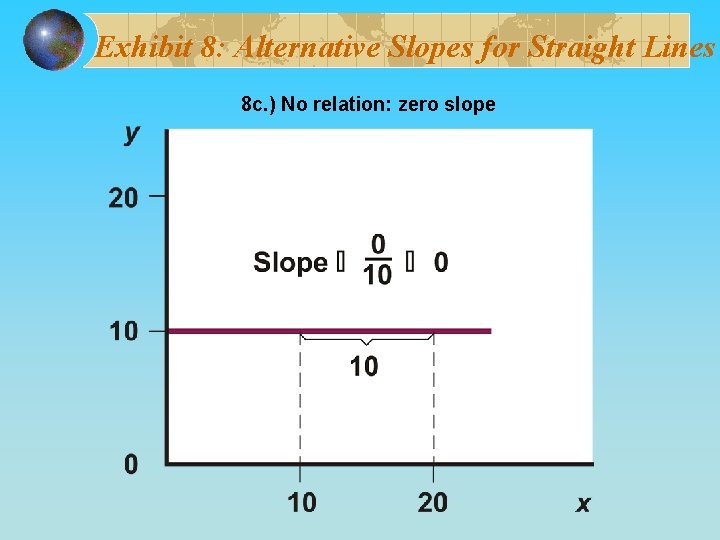
Exhibit 8: Alternative Slopes for Straight Lines 8 c. ) No relation: zero slope

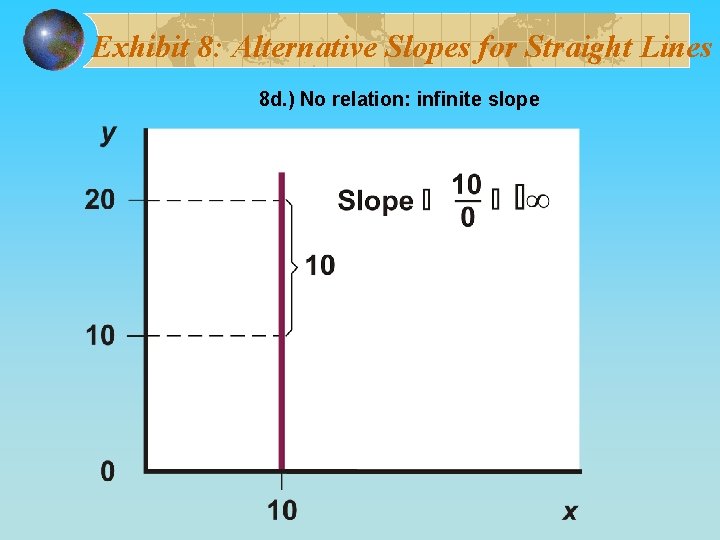
Exhibit 8: Alternative Slopes for Straight Lines 8 d. ) No relation: infinite slope

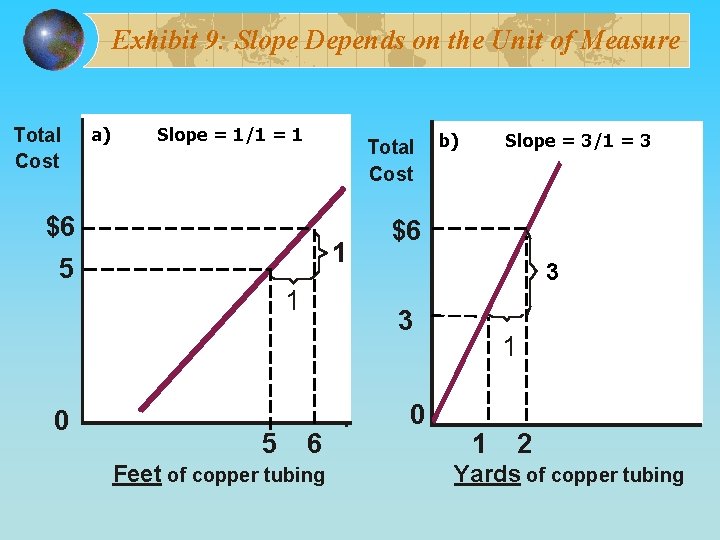
Exhibit 9: Slope Depends on the Unit of Measure Total Cost a) Slope = 1/1 = 1 Total Cost $6 1 5 1 0 5 b) Slope = 3/1 = 3 $6 3 3 6 Feet of copper tubing 0 1 1 2 Yards of copper tubing

Slope and Marginal Analysis Economic analysis usually involves marginal analysis The slope is a convenient device for measuring marginal effects because it reflects the change in one variable – the effect -- compared to the change in some other variable – the cause Slope of straight line is the same everywhere along the line

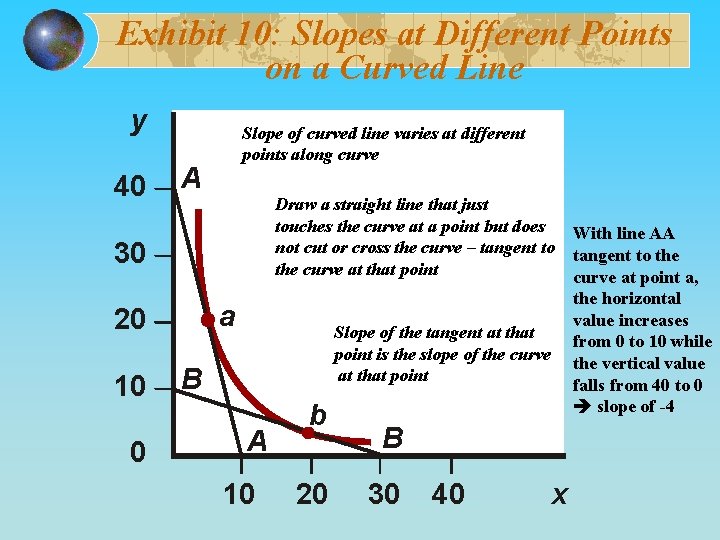
Exhibit 10: Slopes at Different Points on a Curved Line y 40 Slope of curved line varies at different points along curve A Draw a straight line that just touches the curve at a point but does not cut or cross the curve – tangent to the curve at that point 30 a 20 10 0 Slope of the tangent at that point is the slope of the curve at that point B A 10 b 20 B 30 40 x With line AA tangent to the curve at point a, the horizontal value increases from 0 to 10 while the vertical value falls from 40 to 0 slope of -4

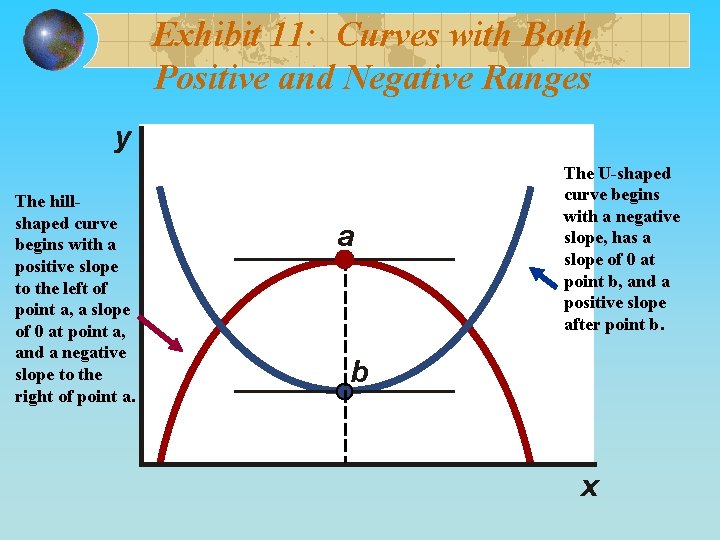
Exhibit 11: Curves with Both Positive and Negative Ranges y The hillshaped curve begins with a positive slope to the left of point a, a slope of 0 at point a, and a negative slope to the right of point a. a The U-shaped curve begins with a negative slope, has a slope of 0 at point b, and a positive slope after point b. b x

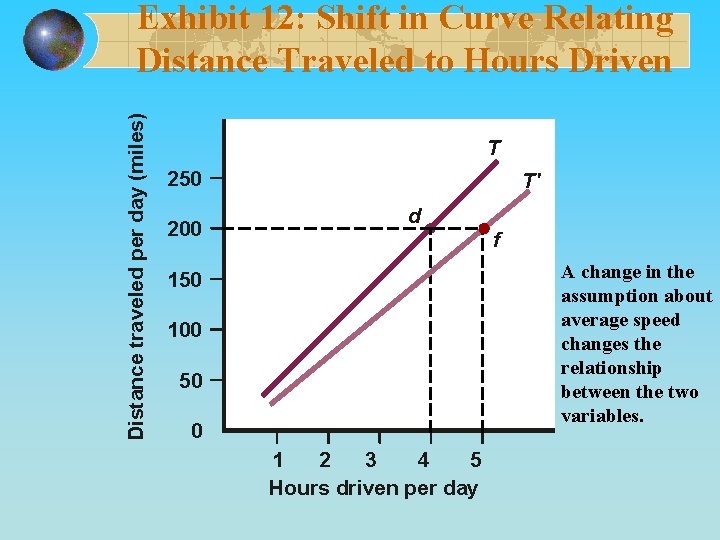
Distance traveled per day (miles) Exhibit 12: Shift in Curve Relating Distance Traveled to Hours Driven T 250 200 T' d f A change in the assumption about average speed changes the relationship between the two variables. 150 100 50 0 1 2 3 4 5 Hours driven per day